20210414-算法学习-树结构(BasicTreeStructure)-多路查找树(muitl-way SearchTree)-(B树,B+树,B*树)-B树篇
一.B树(术语)
1)根节点(root):没有父节点的节点叫做根节点
2)叶子节点(leaf):没有子节点的节点叫做叶子节点
3)内部节点(internal):除根节点和叶子节点之外的节点叫做内部节点,内部节点即有父节点,也有子节点
4)键:B树的存储元素时键,是用于指向数据记录的指针,键的值是用于存储真正的数据记录,一个节点中可以拥有多个键
5)阶:B树的阶为最大子节点数量,其比键的数量大1,一般称一个B树为M阶的B树,那么该B树最多拥有M个子节点,节点中最多拥有M-1个键
二.B树(B-Tree)
1)B树与二叉树(BinaryTree)不是一个概念,B树是一种自平衡的树,能够保持数据有序,这种数据结构能够让查找数据,顺序访问,插入数据及删除动作,都在对数时间内完成
2)B树与AVL树不同,可以拥有2个以上的子节点,并且每个节点可以拥有多个键值,这些属性减少了定位记录时所经历的中间过程,加快了存取速度,B树更适用于读写相对较大的数据块存储系统,如磁盘,B树这种数据结构常被应用在数据库和文件系统的实现上
3)对于一个M阶B树具有以下特征
*每个节点最多有M个子节点,每个内部节点最少有 [M/2] 个子节点([X]为向上取整符号),如果根节点不是叶子节点,那么他至少有两个子节点
*具有 N 个子节点的非叶子节点拥有 N-1 个键
*所有叶子节点必须处于同一层上
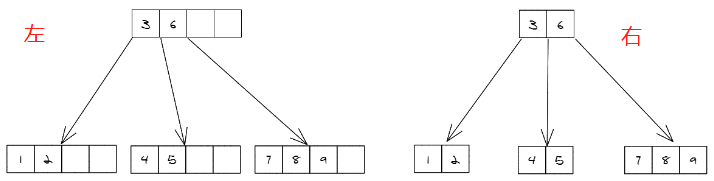
4)如下图,是一棵5阶B树的两种画法,最准确的画法应该是左图B树,但是为了方便,通常会将节点中键为空的位置省去不画,如右图B树,不能因为右图中最多的键为3,就判断这是一颗4阶B树,B树的阶是预先定义好的
三.B树的操作
1)在对B树进行操作时,可能会违反B树的特征如最小子节点数、每个节点最小键数。为了维护B树的这些特性,树可能会分裂或合并,下面我们会以一棵5阶B树来讲述其搜索、插入、删除操作
2)先来看下5阶B树的特性:
*内部节点至少有3个子节点(⌈5/2⌉ = 3),最多有5个子节点
*每个节点至少有2个键(3-1=2),最多有4个键
四.B树的搜索,插入,删除
1)搜索:B树的搜索和二叉搜索树类似,从根节点开始,从上往下递归的遍历树,在每一层节点上,使用二分查找法匹配目标键,或者通过键的范围来确定子树
2)插入:对于新元素的插入,都是发生在叶子节点上的,所有的插入操作都是从根节点开始,搜索这棵树,并找到该元素应该被插入的节点。将新元素插入到该节点需要如下步骤
*如果该节点上的元素数未满,则将新元素插入到该节点,并保持节点中元素的顺序
*如果该节点上的元素已满,则需要将该节点平均地分裂成两个节点:
*从该节点中的元素和新元素先出一个中位数
*小于中位数的元素放到左边节点,大于中位数的元素放到右边节点,中位数做为分隔值
*分隔值被插入到父节点中(增加了树的高度),这可能会导致父节点的分裂,分裂父节点时又可能会使它的父节点分裂,以此类推
*如果分裂一直上升到根节点,那么就创建一个新的根节点,它有一个分隔值和两个子节点。(这就是根节点并不像内部节点一样有最少子节点数量限制的原因)
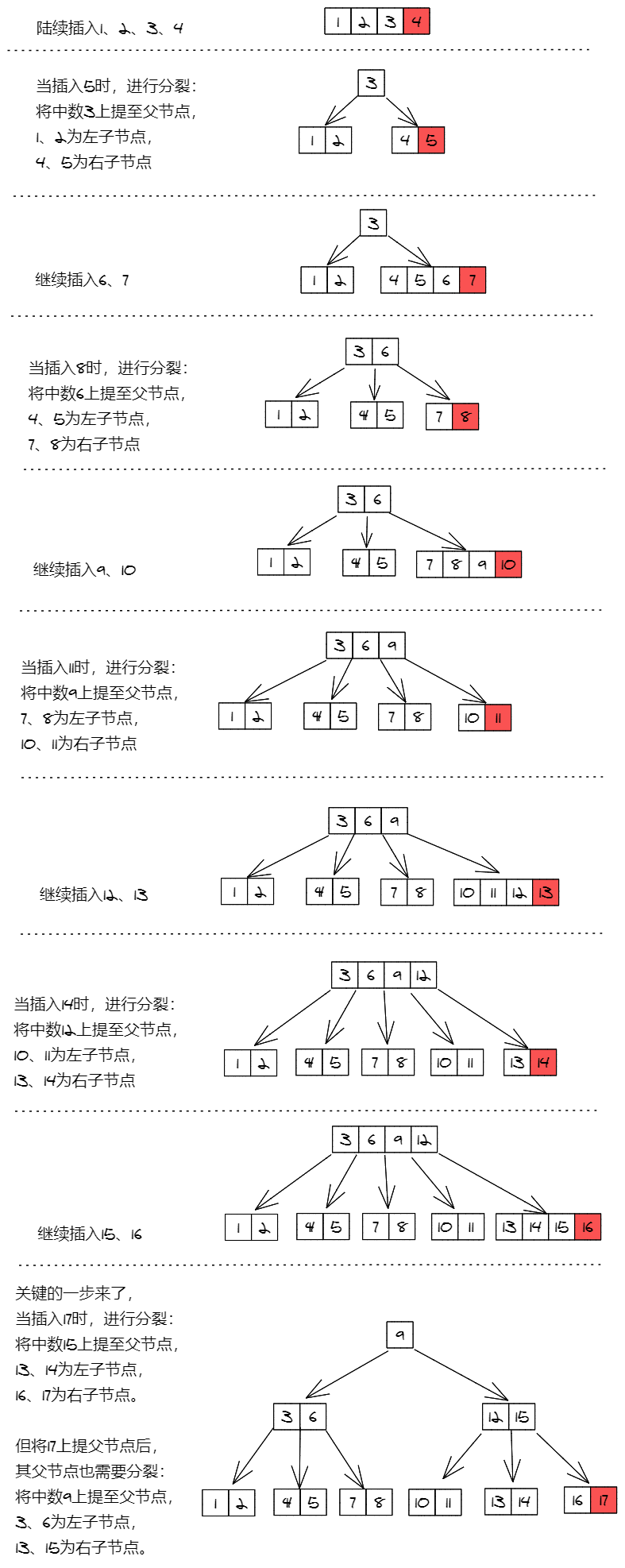
3)下图是一个5阶B树,我们通过顺序插入1到17,来观察节点的分裂过程:
4)删除,B树的删除就复杂了许多,可分为下面几种情况:
1)删除叶子节点中的元素:
*搜索要删除的元素
*如果他在叶子节点上,直接将其删除
*如果删除后产生了下溢出(键数小于最小值),则向其兄弟节点借元素,即将其父亲节点元素下移至当前节点,将兄弟节点中元素上移至父亲节点(若左节点,上移最大元素,若是右节点,上移最小元素)
*若兄弟节点也达到下限,则合并兄弟节点与分割键
2)删除内部节点中的元素
*内部节点中元素为其左右子节点的分割值,需要从左子节点最大元素或右子节点最小元素 中选出一个新的分割符,被选中的分割符从原 子节点中删除,作为新的分割值替换掉被删除的元素
*【上一步中】若左右子节点元素均达到下限,则合并左右子节点
*若删除元素后,其中节点元素小于下限,则继续合并
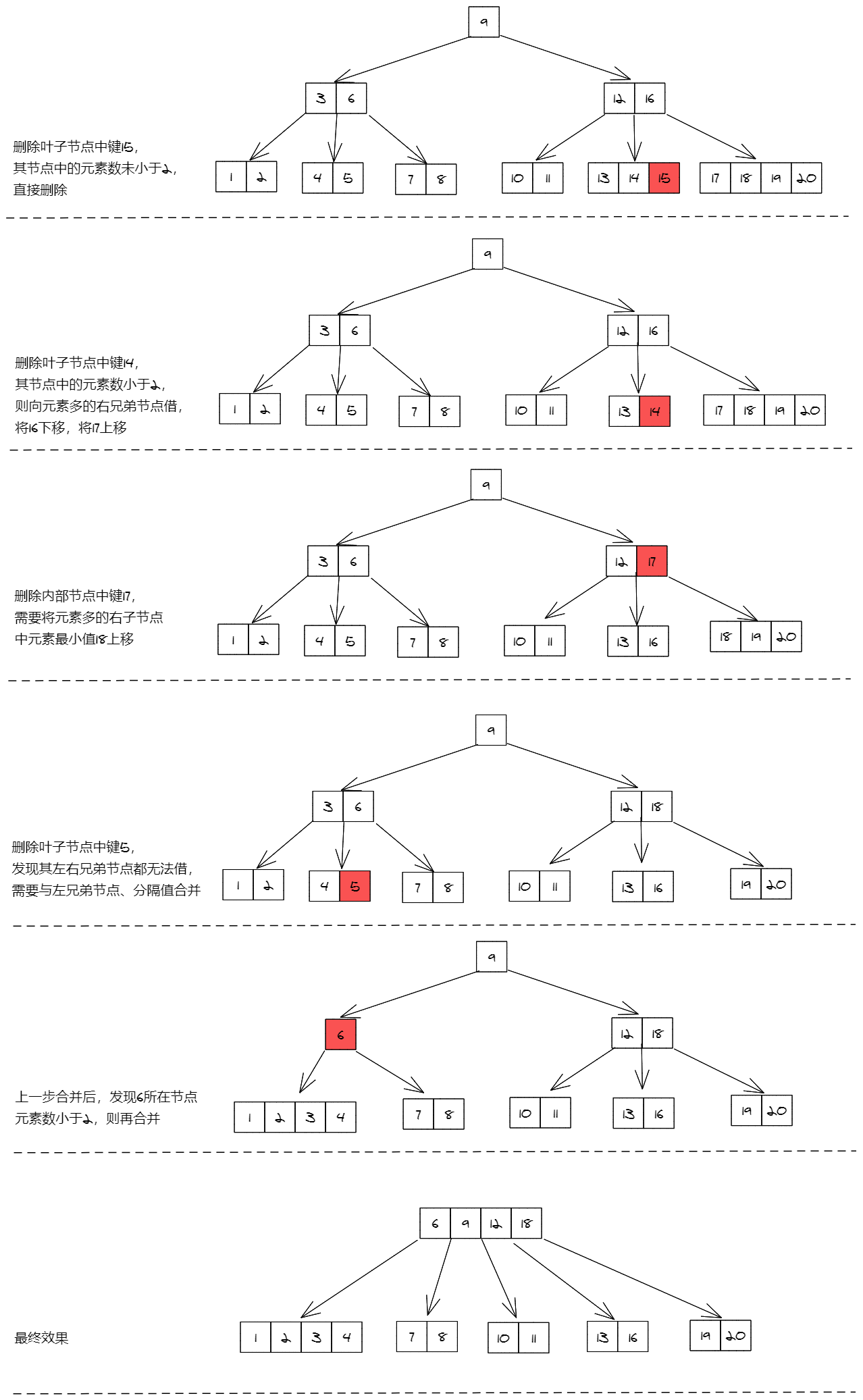
5)下图是一个5阶B树,我们通过删除15、14、17、5四个键,来观察删除过程(基本涵盖所有情况):
五.代码实现:本代码实现了B树的搜索、插入、删除操作,下面看详细介绍
1)键值类,该类用于存放B树每个节点中的键值数据
*key:节点中的键,用于指向数据记录
*value:值,指向的是数据记录
*由于键在节点中是顺序存储的,所以实现了 CompareTo接口
class Entry implements Comparable<Entry> {
final int key;
String value;
@Override
public int compareTo(Entry o) {
return Integer.compare(key, o.getKey());
}
}
2)节点类,节点类是B树中的每个节点,其包括
*entrys:为该节点中所有的子节点,使用List类型存储
*childNodes:为该节点所有的子节点,使用List类型存储
*parentNode:为该节点的父节点
*由于childNodes需要排序,所以该类也实现了 CompareTo接口
*需要明白的一点是,当前节点中每个键的左右子节点都可以通过List集合的下标进行确定,比如:
entrys[0] 的左右子节点分别为childNodes[0],childNodes[1]
entrys[1] 的左右子节点分别为childNodes[1],childNodes[2],以此类推
//B树的节点类
private static class Node implements Comparable<Node> {
private final List<Entry> entrys;//当前节点的键值对
private final List<Node> childNodes;//子节点,使用数组存储于子节点
private Node parentNode;//父节点
public Node() {
entrys = new ArrayList<>();
childNodes = new ArrayList<>();
}
public Node add(Entry entry) {
entrys.add(entry);
Collections.sort(entrys);
return this;
}
public Node addChild(Node node) {
childNodes.add(node);
Collections.sort(childNodes);
return this;
}
@Override
public int compareTo(Node o) {
return Integer.compare(entrys.get(0).getKey(), o.getEntrys().get(0).getKey());
}
}
3)B树类,B树类实现比较复杂,其主要属性包括
*m:为B树的阶
*min:为B树中元素最小值,通过阶 计算出
*root:树的根节点
//B树类
private static class BTree {
private final int m;//B树的阶
private final int mimn;//元素的最小值
private Node root;//树根
public BTree(int m) {
this.m = m;
this.mimn = (int) Math.ceil(m / 2.0) - 1;
}
public Node getRoot() {
return root;
}
}
4)搜索,B树的搜索实现较为简单,在BTree类中添加下面两个方法
*【二分查找】其二分查找法是通过Collections类中的binarySearch方法实现
//根据键搜索数据记录
public Entry searchEntry(int key) {
return searchEntry(root, key);
}
//搜索-递归
public Entry searchEntry(Node node, int key) {
if (node == null) {
return null;
}
//使用二分查找定位下标
int index = Collections.binarySearch(node.getEntrys(), new Entry(key, null));
if (index >= 0) {
return node.getEntrys().get(index);
} else {
if (node.getChildNodes().size() == 0) {
return null;
}
return searchEntry(node.getChildNodes().get(-index - 1), key);
}
}
5)插入,重要是split分离方法,如果添加一个元素后,其节点中元素值超过限定值,则进行分离操作
// 添加元素 - 递归
public void add(Node node, Entry entry) {
//当前节点为叶子节点
if (node.getChildNodes().size() == 0) {
//如果当前节点元素未满,直接添加元素
if (node.getEntrys().size() < m - 1) {
node.add(entry);
return;
}
//如果当前节点元素已满,则分列当前节点
node.getEntrys().add(entry);
// TODO: 2021/4/16 split 分割
return;
}
//当前节点为内部节点,继续往下调用(新插入的节点,只能是叶子节点)
//使用二分查找法找到要插入的分支
int index = Collections.binarySearch(node.getEntrys(), entry);
if (index < 0) {
add(node.getChildNodes().get(-index - 1), entry);
}
}
//*分离当前节点*
private void split(Node node) {
int mid = node.getEntrys().size() / 2;
//分隔值
Entry separateEntry = node.getEntrys().get(mid);
//分离后的左节点
Node leftNode = new Node();
leftNode.getEntrys().addAll(node.getEntrys().subList(0, mid));
//分离后的右节点
Node rightNode = new Node();
rightNode.getEntrys().addAll(node.getEntrys().subList(mid + 1, node.getEntrys().size()));
//分离子节点
if (node.getChildNodes().size() > 0) {
List<Node> leftChildNode = node.getChildNodes().subList(0, m + 1);
for (Node temp : leftChildNode) {
temp.setParentNode(leftNode);
}
leftNode.getChildNodes().addAll(leftChildNode);
List<Node> rightChildNode = node.getChildNodes().subList(mid + 1, node.getEntrys().size() + 1);
for (Node temp : rightChildNode) {
temp.setParentNode(rightNode);
}
rightNode.getChildNodes().addAll(rightChildNode);
}
//当前节点为根节点
if (node.parentNode == null) {
Node newRoot = new Node();
newRoot.add(separateEntry);
root = newRoot;
leftNode.parentNode = root;
rightNode.parentNode = root;
root.addChild(leftNode).addChild(rightNode);
} else {
node.parentNode.add(separateEntry);
leftNode.parentNode = node.parentNode;
rightNode.parentNode = node.parentNode;
node.parentNode.addChild(leftNode).addChild(rightNode);
node.parentNode.getChildNodes().remove(node);
//若其父节点溢出,继续分裂
if (node.parentNode.getEntrys().size() > m - 1) {
split(node.parentNode);
}
}
}
6)删除,B树的删除是最麻烦的,出现的情况太多了
*删除的节点主要为内部节点和叶子节点,每删除后都要判断当前节点中元素是否超出下限值,若超出下限值,需要根据情况进行判断
*若删除的是叶子节点,可能会出现操作时 左旋,右旋,合并(当前节点,兄弟节点,中间值进行合并)合并后又会出现其父节点超出下限值
*若删除的是内部节点,可能会出现操作时,合并左右兄弟节点,合并左右兄弟节点与中间值,向兄弟节点借元素,同样合并后也会出现其父亲节点超出下限
//删除
public void remove(int key) {
//先查询出当前元素所在节点
Node node = searchNode(key);
if (node == null) {
return;
}
//删除节点
int keyIndex = Collections.binarySearch(node.getEntrys(), new Entry(key, null));
node.getEntrys().remove(keyIndex);
//若当前节点的键数小于限定值,进行删除后的操作
if (node.getEntrys().size() < min) {
// TODO: 2021/4/17
afterDeletingHandler(node, keyIndex);
}
}
//删除后处理:当前节点元素数小于限定值,则根据不同场景选择进行合并、左旋、右旋
private void afterDeletingHandler(Node node, int deletedKeyIndex) {
//该节点为内部节点
if (node.getChildNodes().size() > 0) {
//获取删除元素的左右子节点
Node leftChideNode = node.getChildNodes().get(deletedKeyIndex);
Node rightChildNode = node.getChildNodes().get(deletedKeyIndex + 1);
int leftEntrysSize = leftChideNode == null ? 0 : leftChideNode.entrys.size();
int rightEntrysSize = rightChildNode == null ? 0 : rightChildNode.entrys.size();
int maxSize = Math.max(leftEntrysSize, rightEntrysSize);
//先向左右节点借
if (maxSize <= min) {
//若左右子节点达到限制,则合并左右子节点
// TODO: 2021/4/17
}
}
}
/**
* 将当前节点与兄弟节点、中间值合并
*
* @param node 当前节点
* @param brotherNode 兄弟节点
* @param parentEntryIndex 中间值
*/
private void merge(Node node, Node brotherNode, int parentEntryIndex) {
//创建新的节点
Node parentNode = node.getParentNode();
Node newNode = new Node();
newNode.getEntrys().addAll(node.getEntrys());
newNode.getEntrys().addAll(brotherNode.getEntrys());
newNode.add(parentNode.getEntrys().get(parentEntryIndex));
//删除原节点及关系
parentNode.getEntrys().remove(parentEntryIndex);
parentNode.getChildNodes().remove(node);
parentNode.getChildNodes().remove(brotherNode);
if (node.getChildNodes().size() > 0) {
for (Node childNode : node.getChildNodes()) {
newNode.addChild(childNode);
childNode.setParentNode(newNode);
}
}
if (brotherNode.getChildNodes().size() > 0) {
for (Node childNode : brotherNode.getChildNodes()) {
newNode.addChild(childNode);
childNode.setParentNode(newNode);
}
}
//若原节点为根节点,则当前节点为新的根节点
if (parentNode.getEntrys().size() == 0) {
root = newNode;
return;
} else {
parentNode.addChild(newNode);
newNode.setParentNode(parentNode);
}
//合并后,若父节点的元素小于限定值,则在合并(原则上是与最少元素节点合并)
if (parentNode.getEntrys().size() < min) {
Node grandfatherNode = parentNode.getParentNode();
if (grandfatherNode == null) {
return;
}
int nodeIndex = Collections.binarySearch(grandfatherNode.getChildNodes(), parentNode);
//左兄弟节点
Node leftNode = nodeIndex > 0 ? grandfatherNode.getChildNodes().get(nodeIndex - 1) : null;
//右兄弟节点
Node rightNode = nodeIndex >= grandfatherNode.getChildNodes().size() - 1 ? null : grandfatherNode.getChildNodes().get(nodeIndex + 1);
int leftEntrysSize = leftNode == null ? 0 : leftNode.entrys.size();
int rightEntrysSize = rightNode == null ? 0 : rightNode.entrys.size();
int minSize = Math.min(leftEntrysSize, rightEntrysSize);
if (minSize > 0) {
if (leftEntrysSize == minSize) {
merge(parentNode, leftNode, nodeIndex - 1);
} else {
merge(parentNode, rightNode, nodeIndex + 1);
}
} else if (leftEntrysSize > 0) {
merge(parentNode, leftNode, nodeIndex - 1);
} else {
merge(parentNode, rightNode, nodeIndex);
}
}
}
/**
* 合并两个兄弟节点
*
* @param node 当前节点
* @param brotherNode 兄弟节点
*/
private void merge(Node node, Node brotherNode) {
Node parentNode = node.getParentNode();
Node newNode = new Node();
newNode.getEntrys().addAll(node.getEntrys());
newNode.getEntrys().addAll(brotherNode.getEntrys());
Collections.sort(newNode.getEntrys());
newNode.setParentNode(parentNode);
parentNode.getChildNodes().remove(node);
parentNode.getChildNodes().remove(brotherNode);
parentNode.addChild(newNode);
}
/**
* 左旋转
* (1)将父节点的中间值元素删除,并添加到当前节点中
* (2)将右兄弟节点中最小元素删除,并添加到父节点中
*
* @param node 当前节点
* @param nodeIndex 中间值索引
* @param rightNode 右节点
*/
private void leftRotate(Node node, int nodeIndex, Node rightNode) {
Entry parentEntry = node.getParentNode().getEntrys().get(nodeIndex);
node.add(parentEntry);
node.getParentNode().getEntrys().remove(parentEntry);
Entry rightEntry = rightNode.getEntrys().get(0);
node.getParentNode().add(rightEntry);
rightNode.getEntrys().remove(rightEntry);
}
/**
* 右旋转
* (1)将父节点的中间值元素删除,并添加到当前节点中
* (2)将左兄弟节点中最大元素删除,并添加到父节点中
*
* @param node 当前节点
* @param nodeIndex 中间值索引
* @param leftNode 左节点
*/
private void rightRotate(Node node, int nodeIndex, Node leftNode) {
Entry parentEntry = node.getParentNode().getEntrys().get(nodeIndex - 1);
node.add(parentEntry);
node.getParentNode().getEntrys().remove(parentEntry);
Entry leftEntry = leftNode.getEntrys().get(leftNode.getEntrys().size() - 1);
node.getParentNode().add(leftEntry);
leftNode.getEntrys().remove(leftEntry);
}
六.代码整合
package com.atAlgorithmTest;
/**
* @Author: lisongtao
* @Date: 2021/4/15 15:30
*/
import com.alibaba.fastjson.JSONObject;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
/**
* @ClassName BTree
* @Description : BTree示例
* @Author DELL
* @Date 2021/04/15 15:30
**/
public class BTreeDemo {
public static void main(String[] args) {
int[] item = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 14, 16, 15, 17, 18, 19, 20, 13};
BTree tree = new BTree(5);
for (int i : item) {
tree.add(new Entry(i, "-->" + i));
}
System.out.println("----------------------打印当前树结构");
System.out.println(JSONObject.toJSONString(tree));
Entry entry = tree.searchEntry(16);
System.out.println("查询键16:" + entry.getValue());
System.out.println("----------------------删除键15");
tree.remove(15);
System.out.println(JSONObject.toJSONString(tree));
System.out.println("----------------------删除键14");
tree.remove(14);
System.out.println(JSONObject.toJSONString(tree));
System.out.println("----------------------删除键17");
tree.remove(17);
System.out.println(JSONObject.toJSONString(tree));
System.out.println("----------------------删除键5");
tree.remove(5);
System.out.println(JSONObject.toJSONString(tree));
}
//B树类
private static class BTree {
private final int m;//B树的阶
private final int min;//元素的最小值
private Node root;//树根
public BTree(int m) {
this.m = m;
this.min = (int) Math.ceil(m / 2.0) - 1;
}
public Node getRoot() {
return root;
}
@Override
public String toString() {
return "BTree[root=" + root + "]";
}
//根据键搜索数据记录
public Entry searchEntry(int key) {
return searchEntry(root, key);
}
//搜索-递归
private Entry searchEntry(Node node, int key) {
if (node == null) {
return null;
}
// 使用二分查找法定位下标
int index = Collections.binarySearch(node.getEntrys(), new Entry(key, null));
if (index >= 0) {
return node.getEntrys().get(index);
} else {
if (node.getChildNodes().size() == 0) {
return null;
}
return searchEntry(node.getChildNodes().get(-index - 1), key);
}
}
/**
* 根据键搜索记录所在节点
*
* @param key
* @return
*/
public Node searchNode(int key) {
return searchNode(root, key);
}
/**
* 根据键搜索记录所在节点 - 递归
*
* @param node
* @param key
* @return
*/
private Node searchNode(Node node, int key) {
if (node == null) {
return null;
}
// 使用二分查找法定位下标
int index = Collections.binarySearch(node.getEntrys(), new Entry(key, null));
if (index >= 0) {
return node;
} else {
if (node.getChildNodes().size() == 0) {
return null;
}
return searchNode(node.getChildNodes().get(-index - 1), key);
}
}
//添加
public void add(Entry entry) {
//root为空,直接创建
if (root == null) {
Node node = new Node();
node.add(entry);
root = node;
return;
}
add(root, entry);
}
// 添加元素 - 递归
public void add(Node node, Entry entry) {
//当前节点为叶子节点
if (node.getChildNodes().size() == 0) {
//如果当前节点元素未满,直接添加元素
if (node.getEntrys().size() < m - 1) {
node.add(entry);
return;
}
//如果当前节点元素已满,则分列当前节点
node.getEntrys().add(entry);
// TODO: 2021/4/16 split 分割
node.getEntrys().add(entry);
split(node);
return;
}
//当前节点为内部节点,继续往下调用(新插入的节点,只能是叶子节点)
//使用二分查找法找到要插入的分支
int index = Collections.binarySearch(node.getEntrys(), entry);
if (index < 0) {
add(node.getChildNodes().get(-index - 1), entry);
}
}
//*分离当前节点*
private void split(Node node) {
int mid = node.getEntrys().size() / 2;
//分隔值
Entry separateEntry = node.getEntrys().get(mid);
//分离后的左节点
Node leftNode = new Node();
leftNode.getEntrys().addAll(node.getEntrys().subList(0, mid));
//分离后的右节点
Node rightNode = new Node();
rightNode.getEntrys().addAll(node.getEntrys().subList(mid + 1, node.getEntrys().size()));
//分离子节点
if (node.getChildNodes().size() > 0) {
List<Node> leftChildNode = node.getChildNodes().subList(0, m + 1);
for (Node temp : leftChildNode) {
temp.setParentNode(leftNode);
}
leftNode.getChildNodes().addAll(leftChildNode);
List<Node> rightChildNode = node.getChildNodes().subList(mid + 1, node.getEntrys().size() + 1);
for (Node temp : rightChildNode) {
temp.setParentNode(rightNode);
}
rightNode.getChildNodes().addAll(rightChildNode);
}
//当前节点为根节点
if (node.parentNode == null) {
Node newRoot = new Node();
newRoot.add(separateEntry);
root = newRoot;
leftNode.parentNode = root;
rightNode.parentNode = root;
root.addChild(leftNode).addChild(rightNode);
} else {
node.parentNode.add(separateEntry);
leftNode.parentNode = node.parentNode;
rightNode.parentNode = node.parentNode;
node.parentNode.addChild(leftNode).addChild(rightNode);
node.parentNode.getChildNodes().remove(node);
//若其父节点溢出,继续分裂
if (node.parentNode.getEntrys().size() > m - 1) {
split(node.parentNode);
}
}
}
//删除
public void remove(int key) {
//先查询出当前元素所在节点
Node node = searchNode(key);
if (node == null) {
return;
}
//删除节点
int keyIndex = Collections.binarySearch(node.getEntrys(), new Entry(key, null));
node.getEntrys().remove(keyIndex);
//若当前节点的键数小于限定值,进行删除后的操作
if (node.getEntrys().size() < min) {
// TODO: 2021/4/17
afterDeletingHandler(node, keyIndex);
}
}
//删除后处理:当前节点元素数小于限定值,则根据不同场景选择进行合并、左旋、右旋
private void afterDeletingHandler(Node node, int deletedKeyIndex) {
//该节点为内部节点
if (node.getChildNodes().size() > 0) {
//获取删除元素的左右子节点
Node leftChideNode = node.getChildNodes().get(deletedKeyIndex);
Node rightChildNode = node.getChildNodes().get(deletedKeyIndex + 1);
int leftEntrysSize = leftChideNode == null ? 0 : leftChideNode.entrys.size();
int rightEntrysSize = rightChildNode == null ? 0 : rightChildNode.entrys.size();
int maxSize = Math.max(leftEntrysSize, rightEntrysSize);
//先向左右节点借
if (maxSize <= min) {
//若左右子节点达到限制,则合并左右子节点
// TODO: 2021/4/17
}
}
}
/**
* 将当前节点与兄弟节点、中间值合并
*
* @param node 当前节点
* @param brotherNode 兄弟节点
* @param parentEntryIndex 中间值
*/
private void merge(Node node, Node brotherNode, int parentEntryIndex) {
//创建新的节点
Node parentNode = node.getParentNode();
Node newNode = new Node();
newNode.getEntrys().addAll(node.getEntrys());
newNode.getEntrys().addAll(brotherNode.getEntrys());
newNode.add(parentNode.getEntrys().get(parentEntryIndex));
//删除原节点及关系
parentNode.getEntrys().remove(parentEntryIndex);
parentNode.getChildNodes().remove(node);
parentNode.getChildNodes().remove(brotherNode);
if (node.getChildNodes().size() > 0) {
for (Node childNode : node.getChildNodes()) {
newNode.addChild(childNode);
childNode.setParentNode(newNode);
}
}
if (brotherNode.getChildNodes().size() > 0) {
for (Node childNode : brotherNode.getChildNodes()) {
newNode.addChild(childNode);
childNode.setParentNode(newNode);
}
}
//若原节点为根节点,则当前节点为新的根节点
if (parentNode.getEntrys().size() == 0) {
root = newNode;
return;
} else {
parentNode.addChild(newNode);
newNode.setParentNode(parentNode);
}
//合并后,若父节点的元素小于限定值,则在合并(原则上是与最少元素节点合并)
if (parentNode.getEntrys().size() < min) {
Node grandfatherNode = parentNode.getParentNode();
if (grandfatherNode == null) {
return;
}
int nodeIndex = Collections.binarySearch(grandfatherNode.getChildNodes(), parentNode);
//左兄弟节点
Node leftNode = nodeIndex > 0 ? grandfatherNode.getChildNodes().get(nodeIndex - 1) : null;
//右兄弟节点
Node rightNode = nodeIndex >= grandfatherNode.getChildNodes().size() - 1 ? null : grandfatherNode.getChildNodes().get(nodeIndex + 1);
int leftEntrysSize = leftNode == null ? 0 : leftNode.entrys.size();
int rightEntrysSize = rightNode == null ? 0 : rightNode.entrys.size();
int minSize = Math.min(leftEntrysSize, rightEntrysSize);
if (minSize > 0) {
if (leftEntrysSize == minSize) {
merge(parentNode, leftNode, nodeIndex - 1);
} else {
merge(parentNode, rightNode, nodeIndex + 1);
}
} else if (leftEntrysSize > 0) {
merge(parentNode, leftNode, nodeIndex - 1);
} else {
merge(parentNode, rightNode, nodeIndex);
}
}
}
/**
* 合并两个兄弟节点
*
* @param node 当前节点
* @param brotherNode 兄弟节点
*/
private void merge(Node node, Node brotherNode) {
Node parentNode = node.getParentNode();
Node newNode = new Node();
newNode.getEntrys().addAll(node.getEntrys());
newNode.getEntrys().addAll(brotherNode.getEntrys());
Collections.sort(newNode.getEntrys());
newNode.setParentNode(parentNode);
parentNode.getChildNodes().remove(node);
parentNode.getChildNodes().remove(brotherNode);
parentNode.addChild(newNode);
}
/**
* 左旋转
* (1)将父节点的中间值元素删除,并添加到当前节点中
* (2)将右兄弟节点中最小元素删除,并添加到父节点中
*
* @param node 当前节点
* @param nodeIndex 中间值索引
* @param rightNode 右节点
*/
private void leftRotate(Node node, int nodeIndex, Node rightNode) {
Entry parentEntry = node.getParentNode().getEntrys().get(nodeIndex);
node.add(parentEntry);
node.getParentNode().getEntrys().remove(parentEntry);
Entry rightEntry = rightNode.getEntrys().get(0);
node.getParentNode().add(rightEntry);
rightNode.getEntrys().remove(rightEntry);
}
/**
* 右旋转
* (1)将父节点的中间值元素删除,并添加到当前节点中
* (2)将左兄弟节点中最大元素删除,并添加到父节点中
*
* @param node 当前节点
* @param nodeIndex 中间值索引
* @param leftNode 左节点
*/
private void rightRotate(Node node, int nodeIndex, Node leftNode) {
Entry parentEntry = node.getParentNode().getEntrys().get(nodeIndex - 1);
node.add(parentEntry);
node.getParentNode().getEntrys().remove(parentEntry);
Entry leftEntry = leftNode.getEntrys().get(leftNode.getEntrys().size() - 1);
node.getParentNode().add(leftEntry);
leftNode.getEntrys().remove(leftEntry);
}
}
//B树的节点类
private static class Node implements Comparable<Node> {
private final List<Entry> entrys;//当前节点的键值对
private final List<Node> childNodes;//子节点,使用数组存储于子节点
private Node parentNode;//父节点
public Node() {
entrys = new ArrayList<>();
childNodes = new ArrayList<>();
}
public List<Entry> getEntrys() {
return entrys;
}
public List<Node> getChildNodes() {
return childNodes;
}
public Node getParentNode() {
return parentNode;
}
public void setParentNode(Node parentNode) {
this.parentNode = parentNode;
}
public Node add(Entry entry) {
entrys.add(entry);
Collections.sort(entrys);
return this;
}
public Node addChild(Node node) {
childNodes.add(node);
Collections.sort(childNodes);
return this;
}
@Override
public int compareTo(Node o) {
return Integer.compare(entrys.get(0).getKey(), o.getEntrys().get(0).getKey());
}
@Override
public String toString() {
return "Node[entrys=" + entrys + ",childNodes=" + childNodes + "]";
}
}
//定位一个键值对,其实现了 Map.Entry<K, V> 接口
private static class Entry implements Comparable<Entry> {
final int key;
String value;
public Entry(int key, String value) {
this.key = key;
this.value = value;
}
public int getKey() {
return key;
}
public String getValue() {
return value;
}
public void setValue(String value) {
this.value = value;
}
@Override
public int compareTo(Entry o) {
return Integer.compare(key, o.getKey());
}
}
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号