20210325-算法学习-程序员常用的10种算法(Algorithm)-暴力匹配算法(BruteForce)

一.暴力匹配算法

　　1.字符串匹配是我们在编程中常见的问题，其中从一个字符串(主串)中检测出另一个字符串(模式串)是一个非常经典的问题，当提及到这个问题时我们首先想到的算法可能就是暴力匹配，下面的动图就展示了暴力匹配的流程

　　

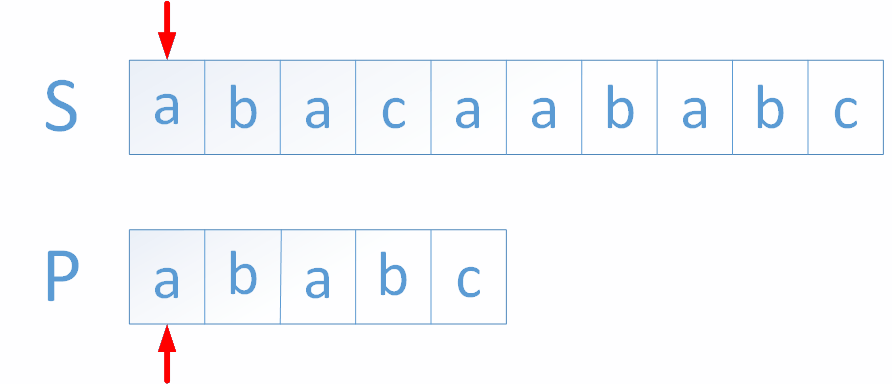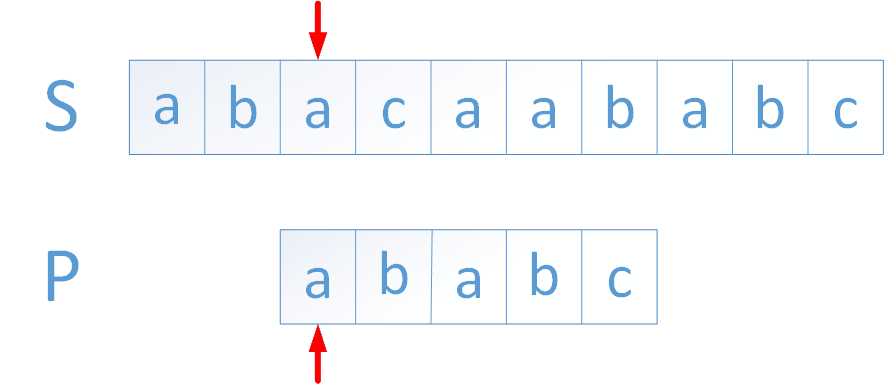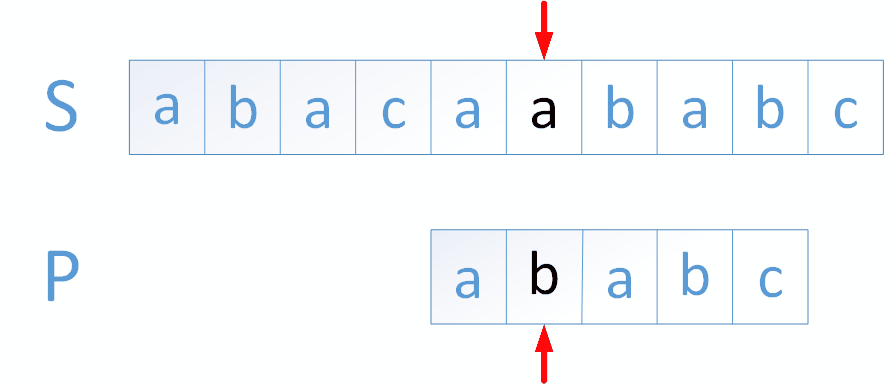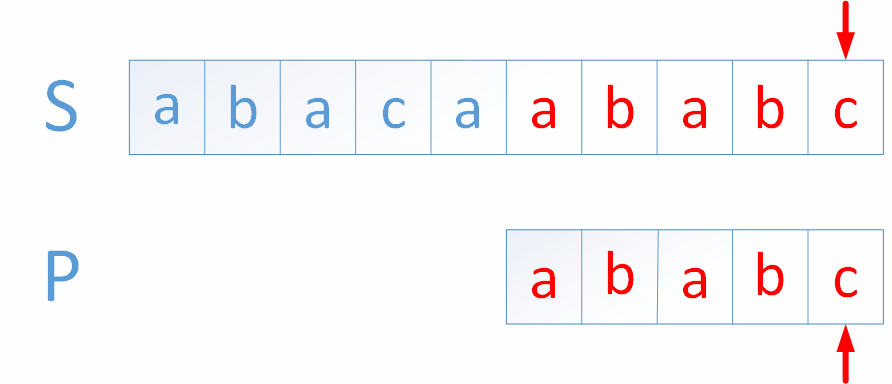
　　　　*上图中箭头指向的字符都为蓝色时代表二者匹配，都为黑色时代表二者不匹配，红色则代表在主串中找到模式串

　　　　*这种算法大致思路就是每当模式串和主串中有字符不匹配，模式串与主串对应的位置整体向后移动一位，再次从模式串第一位开始比较

　　　　*重复上述做法直至在主串中匹配到模式串或者匹配到主串最后一位结束

　　　　*如果主串与模式串都比较短时，用暴力匹配还是不错的选择，编码也相对容易；但是如果主串与模式串过长时，我们只是简单想想就知道这个过程是非常耗时

　　

　　2.如果用暴力匹配的思路，并假设现在 str1匹配到 i位置，子串 str2匹配到 j位置，则有:
　　　　*如果当前字符匹配成功(即strl[i]==str2[j])，则i++，j++，继续匹配下一个字符

　　　　*如果失配（即 strl[i]!= str2[j])，令i=i-(j-1)，j=0。相当于每次匹配失败时，i回溯，j被置为0

　　　　*用暴力方法解决的话就会有大量的回溯，每次只移动一位，若是不匹配，移动到下一位接着判断，浪费了大量的时间。(不可行!)

　　3.举个例子：如果给定文本串S“BBC ABCDAB ABCDABCDABDE”，和模式串P“ABCDABD”，现在要拿模式串P去跟文本串S匹配，整个过程如下所示

1）S[0]为B，P[0]为A，不匹配，执行第②条指令：“如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0”，S[1]跟P[0]匹配，相当于模式串要往右移动一位（i=1，j=0）

2）S[1]跟P[0]还是不匹配，继续执行第②条指令：“如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0”，S[2]跟P[0]匹配（i=2，j=0），从而模式串不断的向右移动一位（不断的执行“令i = i - (j - 1)，j = 0”，i从2变到4，j一直为0）

3）直到S[4]跟P[0]匹配成功（i=4，j=0），此时按照上面的暴力匹配算法的思路，转而执行第①条指令：“如果当前字符匹配成功（即S[i] == P[j]），则i++，j++”，可得S[i]为S[5]，P[j]为P[1]，即接下来S[5]跟P[1]匹配（i=5，j=1）

4）S[5]跟P[1]匹配成功，继续执行第①条指令：“如果当前字符匹配成功（即S[i] == P[j]），则i++，j++”，得到S[6]跟P[2]匹配（i=6，j=2），如此进行下去

5）直到S[10]为空格字符，P[6]为字符D（i=10，j=6），因为不匹配，重新执行第②条指令：“如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0”，相当于S[5]跟P[0]匹配（i=5，j=0）

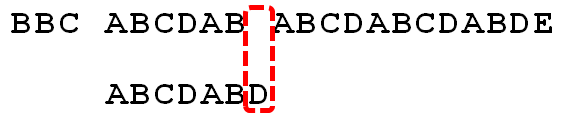
6）至此，我们可以看到，如果按照暴力匹配算法的思路，尽管之前文本串和模式串已经分别匹配到了S[9]、P[5]，但因为S[10]跟P[6]不匹配，所以文本串回溯到S[5]，模式串回溯到P[0]，从而让S[5]跟P[0]匹配。

*而S[5]肯定跟P[0]失配。为什么呢？因为在之前第4步匹配中，我们已经得知S[5] = P[1] = B，而P[0] = A，即P[1] != P[0]，故S[5]必定不等于P[0]，所以回溯过去必然会导致失配。那有没有一种算法，让i 不往回退，只需要移动j 即可呢？
*答案是肯定的。这种算法就是本文的主旨KMP算法，它利用之前已经部分匹配这个有效信息，保持i 不回溯，通过修改j 的位置，让模式串尽量地移动到有效的位置。

 

　　4.暴力匹配算法实现

package com.atAlgorithmTest;
/**
 * @Author: lisongtao
 * @Date: 2021/3/27 10:47
 */


/**
 * @ClassName AlgorithmTest
 * @Description算法练习
 * @Author DELL
 * @Date 2021/03/27 10:47
 **/
public class AlgorithmTest {

    public static void main(String[] args) {
        String str1 = "叮当快药北京技术开发有限公司";
        String str2 = "技术开发";

        int index = violenceMatch(str1,str2);
        System.out.println("index: "+index);
  
        int index2 = violenceMatch2(str1,str2);
        System.out.println("index2: "+index2);

        int index3 = violenceMatch3(str1,str2);
        System.out.println("index3: "+index3);


    }

    //暴力匹配算法,匹配两段字符串(str1,str2)，找出其str2在str1中的位置
    /**
     * @Author lisongtao
     * @Description :
     *      如果当前字符匹配成功（即str1[i] == str2[j])，则i++，j++，继续匹配下一个字符。
     *      如果失配（即str1[i] != str2[j]），令i=i-(j-1)，j = 0。
     *      相当于每次匹配失败时，i回溯，j被置为0.用暴力方法解决问题的话会有大量的回溯，每次只移动一位，若是不匹配，移动到下一位接着判断，浪费了大量的时间
     * @Date 2021/3/27 17:23
     * @Param [str1, str2]
     * @return int
     **/

    public static int violenceMatch(String str1,String str2){
        char[] s1 = str1.toCharArray();//把字符串转成字符数组
        char[] s2 = str2.toCharArray();

        int s1Len = s1.length;
        int s2Len = s2.length;
        int indexStr1= 0;
        int indexStr2 = 0;
        while(indexStr1<s1Len && indexStr2<s2Len){
            if(s1[indexStr1] == s2[indexStr2]){//匹配两个字符数组的长度，输出i++，j++
                indexStr1++;
                indexStr2++;
            }else{
                indexStr1=indexStr1-(indexStr2-1);//只要碰到不匹配的，就要退出循环，重新进行匹配
                indexStr2=0;
            }
        }
        if(indexStr2==s2Len){
            return indexStr1-indexStr2;
        }else{
            return -1;
        }
    }


    //双指针双循环匹配-Double pointer double loop
    /**
     * @Author lisongtao
     * @Description :
     *      外层循环代表目前在原字符串的起始位置，内循环则是真正匹配的，
     *      如果内循环匹配成功的话则返回，失败了就退回到外层循环，这时外指针向下走一位，进行下一次匹配
     * @Date 2021/3/27 17:14 
     * @Param [str1, str2]
     * @return int
     **/
    
    public static int violenceMatch2(String str1,String str2){
        int indexStr1 = str1.length();
        int indexStr2 = str2.length();
        
        for(int i = 0; i<indexStr1; i++){//外层循环
            for(int j = 0; j<indexStr2; j++){//内层循环
                if(str1.charAt(i+j)!=str2.charAt(j))//每次拿i+j个去匹配j如果匹配不到就break
                    break;
                if(j==indexStr2-1)//如果匹配到了，index-1拿到字符串的下标，并返回i
                    return i;
            }
        }
        return indexStr1;//=i
    }

    //回退机制
    public static int violenceMatch3(String str1,String str2){
        int indexStr = str1.length();
        int indexMatch = str2.length();
        int i,j = 0;

        for(i = 0;i<indexStr&&j<indexMatch;i++){
            if(str1.charAt(i)==str2.charAt(j)){//只要匹配到了开头，j就开始记录
                j++;
            }else{//只要碰到一个不行的，j就要退回原型(i也要退回去)
                i -=j;//如果没有匹配到则重新匹配
                j = 0;
            }
        }
        if(j==indexMatch) return i-j;//获取匹配到的下标
        return indexStr;//没有获取到返回原来的字符串
    }
}