CG: 数值微分直线生成算法(DDA)

Abstract

数值微分算法英文全称Digital Differential Analyzer，其直接使用数学微分的概念来进行直线的生成。

思想

在算法中，我们假设直线方程为 \(y = kx + b\) ，斜率 \(k = \frac{dy}{dx}\)

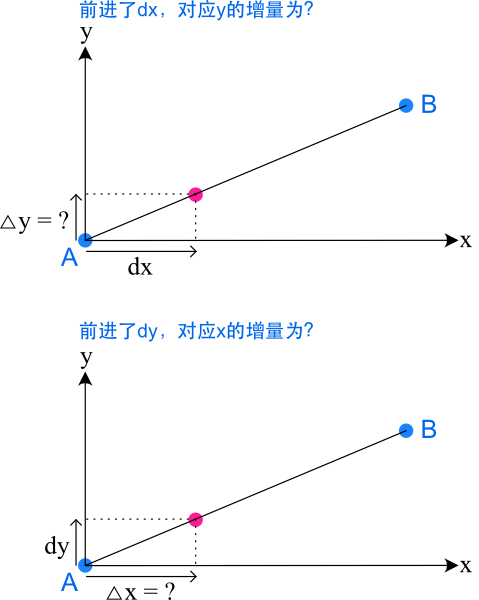
根据微分的思想，在最理想的情况下(也即精度极高，换句话说，\(dx\) 和 \(dy\) 接近无穷小)，每绘制下一个点时，我们会考虑往y轴正向移动\(dy\) 的距离 / 或往x轴正向移动\(dx\)的距

离时，由斜率公式，对应下个点在x轴正向的增量为 \(\Delta x = \frac{dy}{k}\) / 或在y轴正向的增量为\(\Delta y = k * dx\)。则对应下个点的坐标为 \(p_{n+1} = (x_{n}+\frac{dy}{k}, y_{n}+dy)\) 或

\((x_{n}+dx, y_{n}+k * dx)\)

所以在经典微分的情形下，我们在选择绘制下一点时可以随意选择微分的方向（x轴正向或y轴正向），步长为 \(dx\)或\(dy\) 。

矛盾点

但对于现代计算机来说，极高的精度势必带来更高的计算量。所以DDA会选择将微分方向上的移动步长设置为一个较大的数，我们默认这个步长为1，但这会带来一个问题。

以图里的直线为例子：

在这个例子里（\(k < 1\)），两端点A、B之间的X截距明显大于Y截距，所以在默认微分步长为1的情况下，若选择在Y轴正向上进行微分采样，会发现采样点的数量会比在X上的
少很多。

所以这个例子里产生了矛盾：对于直线来说，其可被表示为一段连续的信号，其变化频率可以认为是无穷大，但若选择在Y轴正向上进行步长为1的采样，会造成采样速度远

小于信号变化频率的现象，其后果就是直线的最终绘制精度会降低，也即走样(Aliasing)。

在此例中若选择在X上采样，至少其采样速度大于在Y上采样，绘制精度也会相应有所提高。

算法

有了以上理解后，DDA的核心便是判断端点之间是X的截距大还是Y的截距大，并选择始终在截距更大的方向进行移动，且步长为1。

void DDA(Vector3f begin, Vector3f end)
{
    float x0 = begin.x();
    float y0 = begin.y();
    float x1 = end.x();
    float y1 = end.y();

    float dx = fabs(x1 - x0);
    float dy = fabs(y1 - y0);

    // 选择最大截距方向为步长方向
    float step = std::max(dx, dy);

    // 若step选择的移动方向为x轴，则deltaX = dx / dx = 1，即默认在x方向进行步长为1的移动
    // 同理deltaY = 1
    float deltaX = dx / step;
    float deltaY = dy / step;

    float x = x0, y = y0;

    for(int i = 0 ; i < step ; i++) {
        x += deltaX;
        y += deltaY;
        setPixel(x, y);
    }
}