题目:

题解:
 大佬的题解:
大佬的题解:
#include "cstdio" int n, ans, k; int main() { scanf("%d", &n); k = n + 1; while (k > 1) { ans += k & 1; k >>= 1; } printf("%d\n", ans); k = n + 1; ans = 0; while (k > 1) { if (k == 2) ans++, k--; else if ((k & 3) == 1) ans += ((k >> 2) << 1) - 1, k >>= 2, k++; else if ((k & 3) == 2) ans += ((k >> 2) << 1), k >>= 2, k++; else if ((k & 3) == 3) ans += ((k >> 2) << 1) + 1, k >>= 2, k++; else ans += (k >> 1), k >>= 2; } printf("%d", ans); return 0; }
题解分析:
这个贪心法的确非常巧妙。可是大佬并没有给出详细严谨的解释。不过我基本上把代码中每一行的意思都“翻译”了出来。
(只不过有一点前提还没有严谨地证明:满足要求的红黑树一定可以是完全二叉树。
因为我发现只有基于这个前提,以上代码才有具体的意义,才可以解释通。)
此外还要注意一点:题目里面的N不包括空节点数!这里要注意!
下面分别针对最小值和最大值进行分析:
对于红色节点最小值:
首先根据红黑树的性质可以得到这样的一个理解:将一个黑色节点涂成红色,可以使得经过这个节点的从根到叶的黑路径长度-1(黑路径就是这条路径上黑色节点的个数)。
所以这个地方贪心的意思就慢慢出来了。
不如假设N个节点都是黑色,然后我们要做的是把黑色涂成红色,问题就变成了最少要涂多少个。
为了使得涂的个数最少,则
1.应当使这棵树尽量平衡。(比如一个满二叉树,每条路径的长度都一样——为树的高度)
2.所涂的节点尽量高度要高(因为越高的节点影响的黑路径就越多)
关于第一点,因为,比如一个节点的左右子树的高度不一样,那么可以通过给较高的子树中的某个或某些节点涂红色,从而达到降低其高度的效果。
所以我们考虑的范围就可以缩小到只考虑完全二叉树了。(因为完全二叉树叶子节点的深度最多相差1,而且相同高度的叶子结点都互相邻近(靠在一起这样可以更便于涂红、即更利于第二点的实现)。
emm可能我表述得并不是很好,下面举个例子来加深理解:
比如这样一棵二叉树(空节点没画出来,后面也都不会画出来):
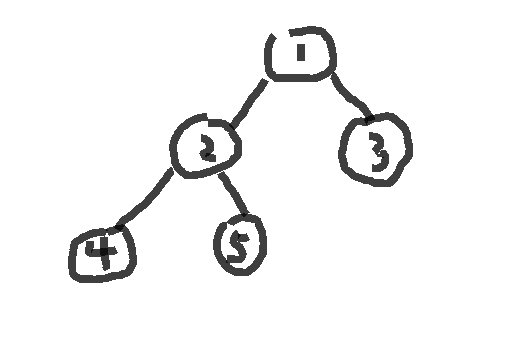
显然,经过节点2的路径要比经过3的长1,所以我们来把一些黑色节点涂成红色来使其符合每条从根要叶子节点的黑路径相同(红黑树的条件也是题目里面的条件)。
我们可以涂4、5:

也可以涂2:
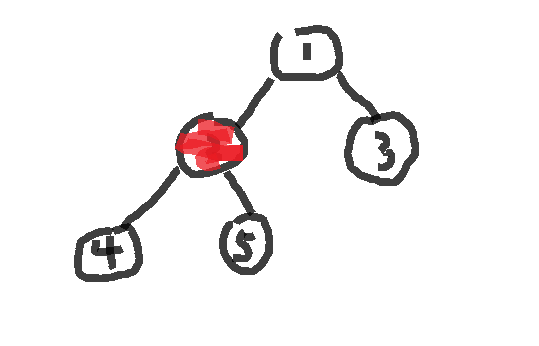
显然,为了使红色节点数最少,此处就会选择涂2号
(慢慢就会发现,每次涂尽量涂高处,这样红色节点影响的路径数才多,红色节点用的自然也就更少了。这里就用了贪心的思想)。
再看个例子:

两棵树看起来都挺平衡的(子树高度差不超过1)(左边为完全二叉树,右边不是)
但是左边的树只要涂一个节点就行了,右边的至少要涂两个。
这也是为什么我们选择完全二叉树来考虑的原因。
然后我们来思考如何求出要涂红的最少的节点数。
不如从例子出发,有这样一棵完全二叉树:
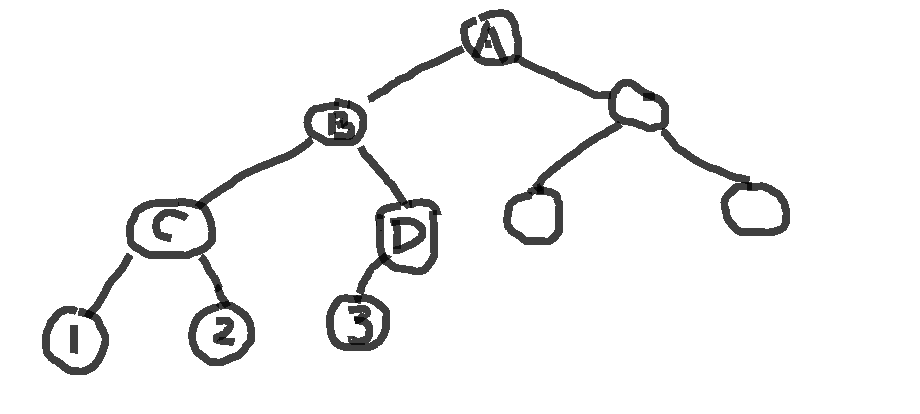
我们要做的就是通过将1、2、3节点或其祖先节点涂红,把节点1、2、3的深度调整到和右半棵树相同(即深度-1)。
为了贪心,我们从上往下考虑:
A节点:不行,因为他会影响到不需要调整的节点。
B节点:不可行,因为他会影响到不需要调整的节点(图中看不出来是因为,它影响的是空节点(空节点算是黑色,但是上图我没把他画出来))。
C节点:可行
D节点:可行
此时以及全部符合要求
综上只最少需要涂两个。
通过自己具大量的例子,可以发现这样一个规律:完全二叉树,设最下面一层节点数为m,且最下面一层未满。
当m=1时,只需要涂1个,
当m=2时,只需要涂1个,
当m=4时,只需要涂1个,
······
当m = 2的n次方时,只需要涂1个。
此时可以停下来,慢慢结合满二叉树的性质来思考思考这件事情。
没错,这里就利用到了,满二叉树的叶子节点数等于2的幂。
例如下面的例子,此时红色涂的就是这连续的2^2个节点作为叶子节点的一个满二叉树的根节点:
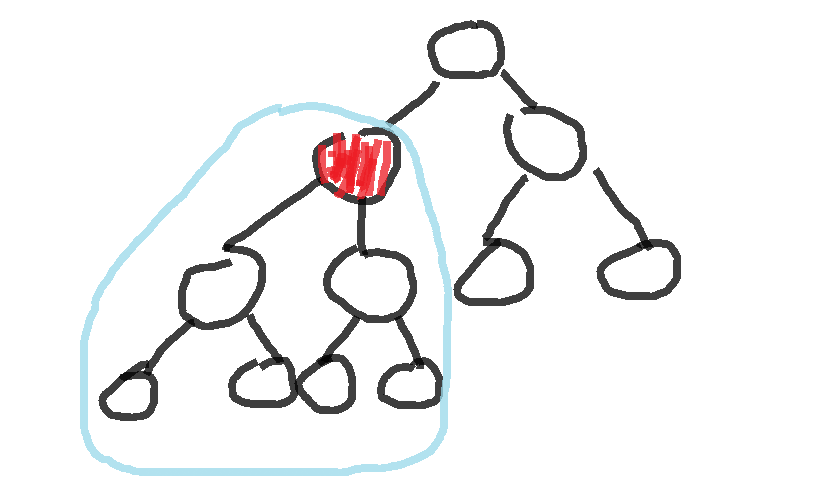
那么下面就可以考虑m不为2的幂的情况了。
例如前一个例子,m=3;
此时可以发现3=1+2 = 2^0 + 2^1 ,此时的答案是 涂2个
再举个例子,这棵树m=7:

7 = 1 + 2+7 = 2^0 + 2 ^ 1 + 2^2 ,而此时的答案是3;
所以,看到这里,即使我的废话可能表述不清,这么多的例子应该能让你有个大概的理解了。



