又在折磨自己

过年好，但我最近真的好想死，听说卡尔曼吕波很重要，为了让自己死得快一点来学学卡尔曼吕波，我对我接下来的半个月充满了绝望。

新年第一天就这么丧可不好，振作起来，人活着总要学会开开心心的，然后少管一些不开心的事情，心里要多装自己少装别人，因为别人的认可其实也并没有多么重要，希望今年不要再做这些伤害自己的事情了。

但无论如何大家还是一点错都没有，今年认识了很多很好的人，新年也受到了很多很多祝福甚至专属红包，有时候觉得大家这么好我还把自己的精神状态搞得这么坏真是对不起大家。

但！无论如何！不开心的时候也是有的，开心的时候也是有的，那么不开心的时候就干坐着等不开心变成开心，那其实也挺好的。事情也是都可以解决的，不能当逃兵，高三的时候即使密炼天天倒数也没有说服自己把密炼旷了，说明我逆商已经很高了！

然而我上学期没学线性代数，寄，我把公式扔在这就跑。

简易的理解

假如有一辆小车儿在路上行驶，你想给这个小车儿做定位，现在你有两种选择：

观测值：直接使用 GPS 定位，然而每次获取的位置都有随机误差。
估计值：通过之前的观察你发现这个小车儿正在做匀加速直线运动，并且你通过之前的数据推导出了它的速度和加速度，直接用速度和加速度计算出下一时刻的位置。

然而真实情况下小车儿也不一定严格做匀加速直线运动，你发现两种选择都有误差也有一定的可信度，你决定两边都信一点，于是你把观测值和估计值分别乘上一个（加和为 \(1\) 的）系数得到最佳估计值，作为对小车儿真实位置的估计。

现在你要解决的问题是，系数怎么取比较优，或者说，每个时刻的系数分别怎么取比较优。

两边都有不确定性，我们可以认为这个不确定性成正态分布，y 表示真实值为 x 的概率（也就是说函数和 x 轴围成的面积为 \(1\)）。

大概这样

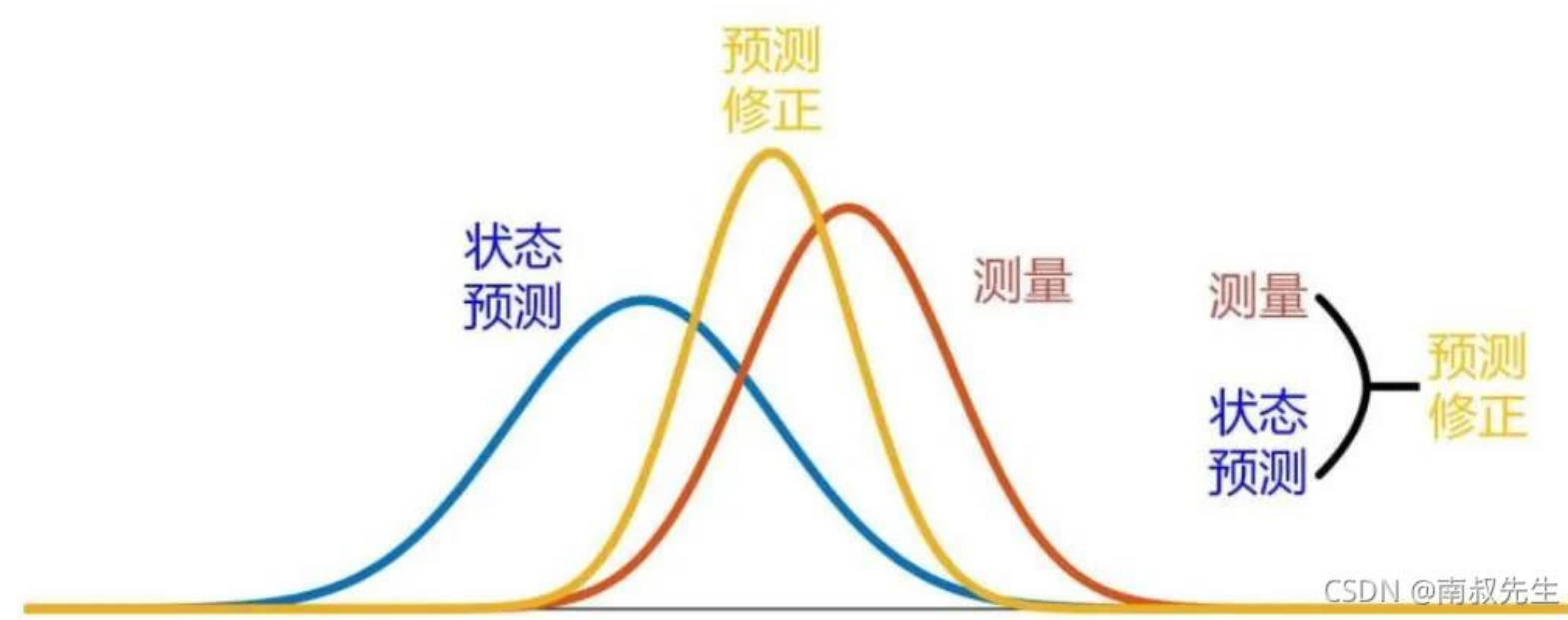
感性地想，肯定是谁的不确定性小谁的系数就取得更大一些。

设置状态

我们将小车儿在 \(t\) 时刻的状态表示为 \(x_t=\left[\begin{array}{c}p_t \\v_t\end{array}\right]\)，其中 \(p_t\) 表示位置，\(v_t\) 表示速度。

那么就有 \(p_t=p_{t-1}+v_{t-1}\times \triangle t + u_{t-1}\times\frac{\triangle t^2} 2\)，其中 \(u_t\) 表示 \(t\) 时刻的加速度，我们假设加速度是可以从驾驶员那里直接得到的。

以及 \(v_t=v_{t-1}+u_{t-1}\times\triangle t\)。

表示成矩阵：

\[\left[\begin{array}{c}p_t \\v_t\end{array}\right] = \left[\begin{array}{c}1&\triangle t \\0&1\end{array}\right] \left[\begin{array}{c}p_{t-1} \\v_{t-1}\end{array}\right] + \left[\begin{array}{c}\frac{\triangle t^2}2 \\{\triangle t}\end{array}\right] u_{t-1} \]

豪德，那我们设

\[F_t=\left[\begin{array}{c}1&\triangle t \\0&1\end{array}\right],~ B_t=\left[\begin{array}{c}\frac{\triangle t^2}2 \\{\triangle t}\end{array}\right] \]

于是得到了简化版小车儿运动公式：\(x_t=F_t x_{t-1}+B_t u_{t-1}\)

那我们就可以用这个公式来计算估计值了，为了把估计值和真实值区分开，我们用 \(x_t\) 表示真实值，用 \(\hat x_t^-\) 表示估计值，用 \(\hat x_t\) 表示最终估计值（也就是估计值和观测值合成的最佳估计值）。

估计值的计算公式：

\[\hat x_t^- = F_t \hat x_{t-1} + B_tu_{t-1} \]

协方差矩阵

但上面说到，“肯定是谁的不确定性小谁的系数就取得更大一些”，因此要想计算系数肯定也要把不确定性用矩阵表示出来。

那聪明的人就想到了，既然是正态分布，可以用方差！

好的，我们确实用方差描述正态分布。但有一个小问题：如果有两个维度怎么办？

一堆点在两个维度上成正态分布是这样的，那么在每一维上都会成正态分布，似乎两个方差就够了。

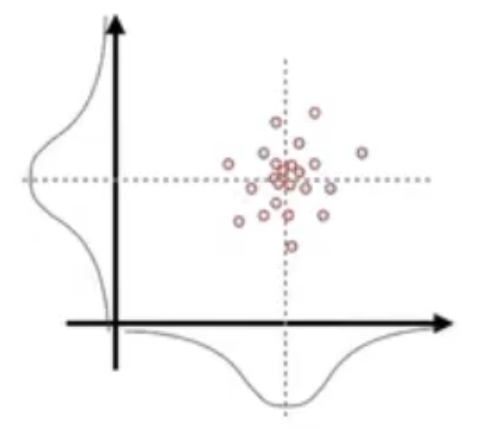
但，如果是下图这样的情况，点在每一维上仍然成正态分布，我们发现仅仅两个方差是不够的，还需要一个新的值，大概是表示 x 维度和 y 维度的关系。

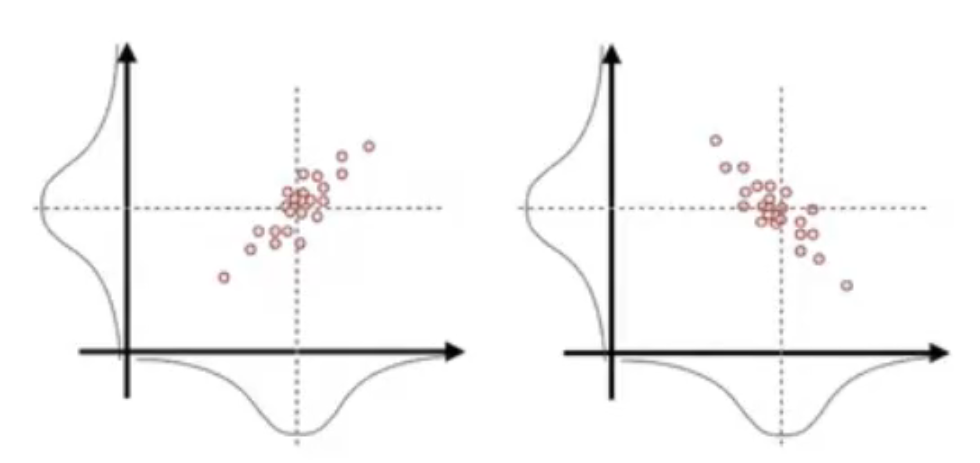
就比方说，假设你发现小车儿的不确定性受小石子的影响，而被小石子绊到时速度和路程都会突然增大，有了这个小性质我们的不确定性就不是简单的只跟某一维有关。

因此我们用矩阵记录不确定性 —— 矩阵可以包含每两维之间的关系。

好的，协方差矩阵的大小就是维度的数量，数量和你设的状态的维数相同（在本文的例子中有 \(p\) 和 \(v\) 两维）。每个位置表示的都是其中两维的关系。也就是说，对角线表示的是自己和自己的关系，也就是这一维的方差啦。

协方差矩阵的传递公式：

\[P_t^-=FP_{t-1}F^T+Q \]

其中 \(P_t\) 表示 \(t\) 时刻的协方差矩阵，右上角带个减号还是因为它只是初步估计值，\(F\) 表示上文提到过的状态转移矩阵，\(F^T\) 表示矩阵的转置。\(Q\) 是这些关系转移的时候难免也会产生噪声，因为关系也不会按照完美的公式变化。

观测矩阵

设 \(z_t\) 为 GPS 在 \(t\) 时刻观测到的小车儿的位置。注意，虽然小车儿的状态有路程和速度两维，但这里速度只是用来辅助计算的，路程才是能够观测的。

既然如此，我们把 “路程才是能够观测的” 这句话也表示成矩阵。设 \(z_t=Hx_t+R\)，其中 \(H\) 就是观测矩阵，此处它的值是 \([1~0]\)，表示如何把你设计的状态转化为观测到的状态。而 \(x_t=\left[\begin{array}{c}p_t \\v_t\end{array}\right]\)，\(R\) 是观测噪声的协方差矩阵，在这里观测值只有一个因此乘起来是一个数字 \(R\) 也是一个数字。

那这个 \(H\) 只有 \([1~0]\) 在这里看起来有点蠢……但其实，假设你实际测量中观测到的路程不是简单的一个 \(z_t\)，而是一堆奇奇怪怪的参数，并且这些参数可能又跟你状态里的好几维都有关，你只知道状态 \(x\) 对每个参数的影响，这时候 \(H\) 就是一个比较复杂的矩阵了，卡尔曼滤波器的数据融合功能也是在这里体现出来的。

状态更新

变量认识全了开始更新状态：

\[\hat x_t=\hat x_t^-+K_t(z_t-H\hat x_t^-) \]

理解一下，加号前面是估计值，后面是根据观测值修正的过程，修正完得到最终估计值。

修正过程中乘的这个系数 \(K_t\) 非常重要，它叫卡尔曼系数，当然也就是我们在最开头提出的，系数怎么取最优的问题。

卡尔曼系数的公式：

\[K_t=P_t^-H^T(HP_t^-H^T+R)^{-1} \]

卡尔曼系数由观测值和估计值的协方差矩阵来决定，对应了最开始说的 “肯定是谁的不确定性小谁的系数就取得更大一些”。

然后还差最后一个公式，从 \(P_t^-\) 到 \(P_t\) 的转移：

\[P_t=(I-K_tH)P_t^- \]

完整公式

预测：