考研路茫茫——早起看书

Problem Description

考研并不是说说就可以了，要付诸于行动。
对于Lele来说，最痛苦的事莫过于早起看书了，不过为了考研，也就豁出去了。由于早起看书会对看书效率产生影响，所以对于要什么时候起床看书，还是有必要考虑的。
经过周密的调查，Lele发现早起的时间会对上午和下午的看书效率都产生影响，具体如下：
他把早起的程度标记为一个非负有理数X，X数值越大，表示越早起。
1.对上午的影响F：符合 F = N / (X^2) 。其中N是一个参数。即越早起床，对上午的效率影响越少。
2.对下午的影响Y：一般越早起，对下午的效率影响越大。不过Y和X的关系比较复杂，并且在不同时候关系也是不同的，于是Lele把它绘制成为函数图形了。在某天，函数图形如下。

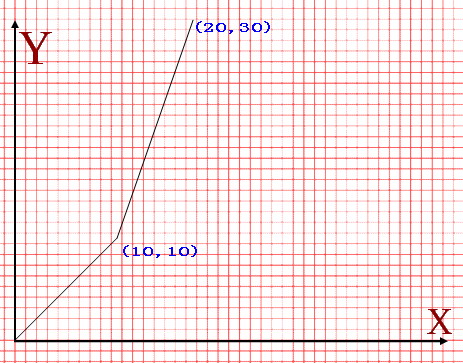
X轴的值表示早起的程度，Y轴的值表示对下午看书效率的影响。函数图像为折线上升的。
不过由于N值和Y-X的图像并不确定，所以Lele每次都要进行大量工作，来确保对整天的看书效率影响最小(F+Y的值最小)，现在就请你帮帮他吧。
记住早起时间的取值X一定要在折线包含的范围之内。(对于上面这个图象，X一定要在[0,20]之内)。

 

 

Input

本题目包含多组输入，请处理到文件结束。 每组测试第一行包含两个整数M和N(1<M<10000,0<=N<=2^31)。其中M表示X-Y图像中顶点的数目。N含义见题目描述。 接下来有M行整数，分别表示这M个点在图像中的坐标Xi和Yi，Xi和Yi范围在[0,2^30]之内。
注意，第一个坐标一定为(0,0)，并且X坐标和Y坐标是不降的，即对于任意 i<j Xi<Xj 且 Yi<=Yj。
而Lele早起的时间一定在[0,Xm-1]这个范围之内。

 

 

Output

对于每组数据，请在一行内输出可能取到的对全天效率(Y+F)影响的最小值。 结果保留三位小数

 

 

Sample Input

3 1 0 0 10 10 20 30 2 1000 0 0 10 10

 

 

Sample Output

1.890 20.000

题意：分段函数求最值。每一段都是一个单峰函数很明显用三分

#include<iostream>
#include<stdio.h>
using namespace std;
int n,m;
int a[10005];
int b[10005];
double ss;
double lmx(double x,int i)
{
    double d=(b[i+1]-b[i]+0.0)/(a[i+1]-a[i]);
    return m*1.0/(x*x)+d*(x-a[i])+b[i];
}
int main()
{
    int i;
    double l,r,mid1,mid2,s;
    while(scanf("%d %d",&n,&m)!=EOF)
    {
        ss=1e30;
        for(i=0;i<n;i++)
        {
            cin>>a[i]>>b[i];
        }
        for(i=0;i<n-1;i++)
        {
            l=a[i]*1.0;
            r=a[i+1]*1.0;
            while(r-l>1e-8)
            {
                mid1=(l+r)/2;
                mid2=(mid1+r)/2;
                if(lmx(mid1,i)<lmx(mid2,i))  r=mid2;
                else l=mid1;
            }
            s=lmx(mid1,i);
            if(s<ss) ss=s;
        }
        printf("%.3lf\n",ss);
     }
     return 0;
}