hdu3480 Division（dp平行四边形优化）

题意：将n个数分成m段，每段的代价为最大值减最小值的平方，为代价最小是多少n<=10000 ,m<=5000

题解：先拍好序，从小到大，这样绝对是花费最小的，不过怎么样来做呢？一定很容易想到dp

分段dp十分好想吧，f[i][j]表示前i个数，分成j个数的最小值。

w[i][j]区间包含性十分好证明，

平行四边不等性，可以很好证明，

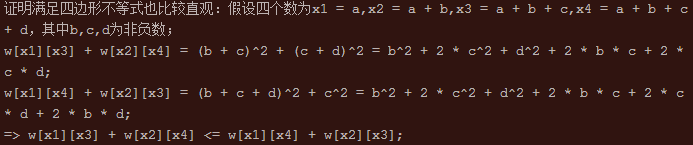
对吧，这样很好理解

所以得出f[i][j]满足------>s[i][j-1]<=s[i][j]<=s[i+1][j]

这个得出来就ok了，但是这道题有点奇葩，s[i][j-1]以前就求好了，但是s[i+1][j]呢？所以

需要倒着dp，先求s[i+1][j]在去搞s[i][j];

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdlib>
#define inf 2000000009
using namespace std;

int cas,n,m,now=0;
int a[10007];
int f[10007][5007],s[10007][5007];

int main()
{
    scanf("%d",&cas);
    while(cas--)
    {
        scanf("%d%d",&n,&m);
        for (int i=1;i<=n;i++)
            scanf("%d",&a[i]);
        sort(a+1,a+n+1);
        for (int i=1;i<=n;i++)
            f[i][1]=(a[i]-a[1])*(a[i]-a[1]),s[i][1]=1;
        for (int k=2;k<=m;k++)
        {
            s[n+1][k]=n;
            for (int i=n;i>=k;i--)
            {
                f[i][k]=inf;
                for (int j=s[i][k-1];j<=s[i+1][k];j++)
                {
                    int t=f[j-1][k-1]+(a[i]-a[j])*(a[i]-a[j]);
                    if (t<f[i][k]) f[i][k]=t,s[i][k]=j;    
                }
            }
        }
        printf("Case %d: %d\n",++now,f[n][m]);
    }
}