杜教筛+51nod 1239 1244
杜教筛是用来求积性函数前缀和的。但是并不是所有的积性函数都是可以杜教筛的。
这个积性函数必须是可以直接统计的。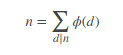
像这样的函数d|n的情况下可以直接统计这样才可以杜教筛。
如何去筛呢?
附上一个大佬的blog

举两道题目吧。
51Nod1239
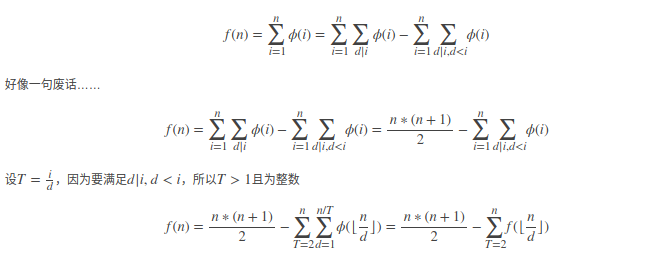
应该可以理解的。
代码附上。
1 #pragma GCC optimize(2) 2 #pragma G++ optimize(2) 3 #include<iostream> 4 #include<cmath> 5 #include<algorithm> 6 #include<cstdio> 7 #include<cstring> 8 9 #define N 2000007 10 #define hash_num 1333333 11 #define mod 1000000007 12 #define ll long long 13 #define ni 500000004LL 14 using namespace std; 15 inline ll read() 16 { 17 ll x=0,f=1;char ch=getchar(); 18 while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} 19 while(isdigit(ch)){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();} 20 return x*f; 21 } 22 23 ll n; 24 int p[N],prime[N],tot; 25 int cnt,hed[N],nxt[N]; 26 ll val[N],rea[N],phi[N]; 27 bool flag[N]; 28 29 void add(int u,ll v,ll x) 30 { 31 nxt[++cnt]=hed[u]; 32 hed[u]=cnt; 33 rea[cnt]=v; 34 val[cnt]=x; 35 } 36 void init_phi() 37 { 38 phi[1]=1; 39 for (int i=2;i<N;i++) 40 { 41 if(!flag[i])prime[++tot]=i,phi[i]=i-1; 42 for (int j=1;j<=tot&&prime[j]*i<N;j++) 43 { 44 flag[i*prime[j]]=true; 45 if(i%prime[j]==0) 46 { 47 phi[i*prime[j]]=phi[i]*prime[j]; 48 break; 49 } 50 else phi[i*prime[j]]=phi[i]*phi[prime[j]]; 51 } 52 } 53 for (int i=2;i<N;i++)(phi[i]+=phi[i-1])%=mod; 54 } 55 ll solve(ll n) 56 { 57 if(n<N)return phi[n]; 58 ll ans=0,k=n%hash_num,last; 59 for (int i=hed[k];i!=-1;i=nxt[i]) 60 if(rea[i]==n)return val[i]; 61 for (ll i=2;i<=n;i=last+1) 62 { 63 last=n/(n/i); 64 (ans+=(last-i+1)%mod*solve(n/i)%mod)%=mod; 65 } 66 ans=((n%mod*((n+1)%mod))%mod*ni%mod-ans+mod)%mod;//2的逆元是固定的。 67 add(k,n,ans); 68 // cout<<n<<" "<<ans<<endl; 69 return ans; 70 } 71 int main() 72 { 73 memset(hed,-1,sizeof(hed)); 74 init_phi(),n=read(); 75 printf("%lld",solve(n)); 76 }
对于51Nod1244 是筛μ的。
1 #pragma optimize(2) 2 #pragma optimize(2) 3 #include<cstring> 4 #include<cstdio> 5 #include<cmath> 6 #include<algorithm> 7 #include<iostream> 8 9 #define N 2000007 10 #define hash_num 1333333 11 #define ll long long 12 using namespace std; 13 inline ll read() 14 { 15 ll x=0,f=1;char ch=getchar(); 16 while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} 17 while(isdigit(ch)){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();} 18 return x*f; 19 } 20 21 ll n,m; 22 int p[N],prime[N],tot; 23 int cnt,hed[N],nxt[N]; 24 ll val[N],rea[N],miu[N]; 25 bool flag[N]; 26 27 void init_miu() 28 { 29 miu[1]=1; 30 for (int i=2;i<N;i++) 31 { 32 if(!flag[i]){prime[++tot]=i;miu[i]=-1;} 33 for (int j=1;j<=tot&&i*prime[j]<N;j++) 34 { 35 flag[i*prime[j]]=true; 36 if(i%prime[j]==0) 37 { 38 miu[i*prime[j]]=0; 39 break; 40 } 41 else miu[i*prime[j]]=-miu[i]; 42 } 43 } 44 for (int i=2;i<N;i++)miu[i]+=miu[i-1]; 45 } 46 void add(int u,ll v,ll k) 47 { 48 nxt[++cnt]=hed[u]; 49 hed[u]=cnt; 50 rea[cnt]=v; 51 val[cnt]=k; 52 } 53 ll solve(ll n) 54 { 55 if(n<N)return miu[n]; 56 ll ans=0,k=n%hash_num,last; 57 for (int i=hed[k];i!=-1;i=nxt[i]) 58 if(rea[i]==n)return val[i]; 59 for (ll i=2;i<=n;i=last+1) 60 { 61 last=n/(n/i); 62 ans+=(last-i+1)*solve(n/i); 63 } 64 ans=1-ans; 65 add(k,n,ans); 66 return ans; 67 } 68 int main() 69 { 70 memset(hed,-1,sizeof(hed)); 71 init_miu(),n=read(),m=read(); 72 printf("%lld",solve(m)-solve(n-1)); 73 }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号