暑假集训 7月5日

单调栈

GInger的神罚洛谷U220471

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int>pii;
const int N=2e5+10;
ll a[N],dp[N],ans=-1;
signed main()
{
    int n;
    cin>>n;
    for (int i=1;i<=n;i++)cin>>a[i];
    stack<pii>s;
    s.push({0,0});
    for (int i=1;i<=n;i++)
    {
        while (s.size()&&s.top().first>=a[i])s.pop();
        pii en=s.top();
        s.push({a[i],i});
        dp[i]=dp[en.second]+a[i]*(i-en.second);
        ans=max(ans,dp[i]);
    }
    cout<<ans<<endl;
    return 0;
}

 

滑动窗口（单调队列模板）

（手动模拟更快）

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6+10;
int a[N],q[N];
signed main()
{
    int n,k;
    cin>>n>>k;
    for (int i=0;i<n;i++)cin>>a[i];
    int hh=0,tt=-1;
    for (int i=0;i<n;i++)
    {
        if (hh<=tt&&i-k+1>q[hh])hh++;
        while (hh<=tt&&a[q[tt]]>=a[i])tt--;
        q[++tt]=i;
        if (i>=k-1)printf("%d ",a[q[hh]]);
    }
    puts("");
    hh=0,tt=-1;
    for (int i=0;i<n;i++)
    {
        if (hh<=tt&&i-k+1>q[hh])hh++;
        while (hh<=tt&&a[q[tt]]<=a[i])tt--;//要找到窗口里面最大的值，当当前的数比之前维护的单调队列里面的数大的时候，一定不会取到比它还小的。
        q[++tt]=i;
        if (i>=k-1)printf("%d ",a[q[hh]]);
    }
    puts("");
    return 0;
}

 KMP模板

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6+10;
ll ne[N];
char s[N],p[N];
signed main()
{
    scanf("%s",s+1);
    scanf("%s",p+1);
    int m=strlen(s+1);
    int n=strlen(p+1);
    for (int i=2,j=0;i<=n;i++)
    {
        while (j&&p[i]!=p[j+1])j=ne[j];
        if (p[i]==p[j+1])j++;
        ne[i]=j;
    }
    for (int i=1,j=0;i<=m;i++)
    {
        while (j&&s[i]!=p[j+1])j=ne[j];
        if (s[i]==p[j+1])j++;
        if (j==n)
        {
            printf("%d\n",i-n+1);
            j=ne[j];
        }
    }
    for (int i=1;i<=n;i++)
    printf("%lld ",ne[i]);
    return 0;
}

并查集

团伙洛谷P1892

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2020;
int p[N];
int Find(int x)
{
    if (x!=p[x])p[x]=Find(p[x]);
    return p[x];
}
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int n;
    cin>>n;
    for (int i=1;i<=2*n;i++)p[i]=i;
    int m;
    cin>>m;
    while (m--)
    {
        char op;
        int a,b;
        cin>>op>>a>>b;
        if (op=='F')
        {
            a=Find(a);
            b=Find(b);
            if (a!=b)
                p[a]=b;
        }
        else
        {
            int aa=Find(a);
            int bb=Find(b);
            int c=Find(a+n);
            int d=Find(b+n);
            if (c!=bb)p[c]=bb;
            if (d!=aa)p[d]=aa;
        }
    }
    int ans=0;
    for (int i=1;i<=n;i++)
    {
        if (p[i]==i)ans++;
    }
    cout<<ans<<"\n";
    return 0;
}

图示：

字典树

用map写：
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2020;

signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    map<string,int>mp;
    int n;
    cin>>n;
    while (n--)
    {
        char op;
        cin>>op;
        string x;
        if (op=='I')
        {
            cin>>x;
            mp[x]++;
        }
        else
        {
            cin>>x;
            cout<<mp[x]<<"\n";
        }
    }
    return 0;
}

字典树模板
tip:这里的idx表示的是节点的个数。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+10;
int son[N][26];
int cnt[N],idx;
void Insert(string x)
{
    int p=0;
    for (int i=0;x[i];i++)
    {
        int num=x[i]-'a';
        if (!son[p][num])son[p][num]=++idx;
        p=son[p][num];
    }
    cnt[p]++;
}
int Query(string x)
{
    int p=0;
    for (int i=0;x[i];i++)
    {
        int num=x[i]-'a';
        if (!son[p][num])return 0;
        p=son[p][num];
    }
    return cnt[p];
}
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int n;
    cin>>n;
    while (n--)
    {
        char op;
        cin>>op;
        string x;
        cin>>x;
        if (op=='I')
        {
            Insert(x);
        }
        else if (op=='Q')
        {
            cout<<Query(x)<<"\n";
        }
    }
    return 0;
}

字典树 最大异或对

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+10,M=31*N;//M表示节点个数，有1e5个数，每个数长度最大31
int a[N],son[M][2],idx;
void insert(int x)
{
    int p=0;
    for (int i=30;i>=0;i--)//从30位开始取是因为高位对这题结果影响更大
    {
        int u=x>>i&1;
        if (!son[p][u])son[p][u]=++idx;
        p=son[p][u];
    }
}
int query(int x)
{
    int p=0,res=0;
    for (int i=30;i>=0;i--)
    {
        int u=x>>i&1;
        if (son[p][!u])
        {
            p=son[p][!u];
            res=res*2+!u;
        }
        else
        {
            p=son[p][u];
            res=res*2+u;
        }
    }
    return res;
}
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int n;
    cin>>n;
    for (int i=0;i<n;i++)cin>>a[i];
    int res=0;
    for (int i=0;i<n;i++)
    {
        insert(a[i]);
        int t=query(a[i]);
        res=max(res,a[i]^t);
    }
    cout<<res<<"\n";
    return 0;
}

 

模拟散列表

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=100003;
int h[N],e[N],ne[N],idx;
void insert(int x)
{
    int k=(x%N+N)%N;
    e[idx]=x;
    ne[idx]=h[k];
    h[k]=idx++;
}
bool find (int x)
{
    int k=(x%N+N)%N;
    for (int i=h[k];i!=-1;i=ne[i])
    {
        if (e[i]==x)return 1;
    }
    return 0;
}
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int n;
    cin>>n;
    memset(h,-1,sizeof h);//很容易忘记初始化
    while (n--)
    {
        char op;
        int x;
        cin>>op>>x;
        if (op=='I')
        {
            insert(x);
        }
        else if (op=='Q')
        {
            if (find(x))
            puts("Yes");
            else
            puts("No");
        }
    }
    return 0;
}

双哈希：

双哈希是为了消除原始聚集和二次聚集问题，不管是线性探测还是二次探测，每次的探测步长都是固定的。双哈希是除了第一个哈希函数外再增加一个哈希函数用来根据关键字生成探测步长，这样即使第一个哈希函数映射到了数组的同一下标，但是探测步长不一样，这样就能够解决聚集的问题。

第二个哈希函数必须具备如下特点

• 和第一个哈希函数不一样；
• 不能输出为0，因为步长为0，每次探测都是指向同一个位置，将进入死循环，经过试验得出 stepSize=constant-(key%constant)形式的哈希函数效果非常好，constant是一个质数并且小于数组容量。

双hash的核心思想是，第二步生成一个随机的探测步长。

 

birthday cake（山东省赛）

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define int long long
const int N=4e5+10;
const int P1=1331,P2=1331,N1=1e9+7,N2=1e9+9;
typedef pair<int,int>pii;
#define x first
#define y second
struct node
{
    string s;
    int len;
}a[N];
bool cmp(node a,node b)
{
    return a.len<b.len;
}
pii h[N],p[N];
pii get(int l,int r)
{
    int x=(h[r].x-h[l-1].x*p[r-l+1].x%N1+N1)%N1;
    int y=(h[r].y-h[l-1].y*p[r-l+1].y%N2+N2)%N2;
    return {x,y};
}
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    map<pii,int>mp;
    int n;
    cin>>n;
    for (int i=1;i<=n;i++)
    {
        cin>>a[i].s;
        a[i].len=a[i].s.size();
    }
    sort(a+1,a+1+n,cmp);
    p[0].x=1;
    p[0].y=1;
    for (int i=1;i<N;i++)
    {
        p[i].x=p[i-1].x*P1%N1;
        p[i].y=p[i-1].y*P2%N2;
    }
    int res=0;
    for (int i=1;i<=n;i++)
    {
        string ss=a[i].s;
        ss="#"+ss;
        for (int j=1;j<=a[i].len;j++)
        {
            h[j].x=(h[j-1].x*P1%N1+ss[j])%N1;
            h[j].y=(h[j-1].y*P2%N2+ss[j])%N2;
        }
        for (int j=1,k=a[i].len;j<k;j++,k--)
        {
            if (get(1,j)==get(k,a[i].len))
            {
                res+=mp[get(j+1,k-1)];
            }
        }
        res+=mp[get(1,a[i].len)];
        mp[get(1,a[i].len)]++;
    }
    cout<<res<<"\n";
    return 0;
}

 

个人赛3补题

B - Road to Arabella（博弈）

 

对手有一个正整数n，你有一个正整数k<=n，每一次都能对n执行n-=x,(1≤x≤max(1,m−k));把0摆在对方面前就是赢了。

如此我们很容易想起奇偶性博弈，总能把偶数摆在对方面前，我们就行了，所以对所有n,k；我们要做的是，能不能总是把偶数摆在对方面前。

则当k+1== n，或者k== n，每次都只能减去1，所以n为奇数我们才能总是把偶数摆在对方面前。其余情况我们总能找到一个数让对手变为偶数，而且是k+1== n,或者k== n.也就是对手面临着刚才分析出来的必败局面，我们就赢了。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int t;
    cin>>t;
    while (t--)
    {
        ll n,k;
        cin>>n>>k;
        if (n==k||n-k==1)
        {
            if (n%2)puts("Kilani");
            else puts("Ayoub");
        }
        else puts("Kilani");
        
    }
    return 0;
}

 

D - Meeting Bahosain（数论）
假如这个数列最终能相等，那么他们之间可以任意转化。假如能把a[0]变成a[1]……a[n-2]变成a[n-1]，这个数列最终就能相等。假如能相等，每个元素都能表示成a [ x ] = a [ x − 1 ] + k 1 ∗ b [ 0 ] + k 2 ∗ b [ 1 ] + … … k n − 1 ∗ b [ n − 1 ] a[x]=a[x-1]+k1*b[0]+k2*b[1]+……kn-1*b[n-1]a[x]=a[x−1]+k1∗b[0]+k2∗b[1]+……kn−1∗b[n−1]，a [ x ] − a [ x − 1 ] = k ∗ g c d ( b ) a[x]-a[x-1]=k*gcd(b)a[x]−a[x−1]=k∗gcd(b)。则若a中所有元素的最大公约数若能被所有b中所有元素的最大公约数整除就可以转化。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll gcd(ll a,ll b)
{
    return b?gcd(b,a%b):a;
}
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int n,k;
    cin>>n>>k;
    ll w,ww;
    for (int i=0;i<n;i++)
    {
        ll x;
        cin>>x;
        if (i==0)w=x;//求n个数的最大公因数的方法
        else
        w=gcd(w,x);
    }
    for (int i=0;i<k;i++)
    {
        ll x;
        cin>>x;
        if (i==0)ww=x;
        else
        ww=gcd(ww,x);
    }
    if (w%ww==0||n==1)puts("Yes");
    else puts("No");
    return 0;
}

 

I - Bashar and Hamada（贪心）

给你一个长度为 n 的数组

选k个数，使F=，ai 、aj k个数，i！= j 。求k=2，3，……n时，F的最大值

首先n=2时，肯定选择数组中的最大值和最小值，这样F2=max-min，F2最大
n=3时，在F2的，然后无论选择哪个，假设选取的数是x，F3=F2 + max - x + x - min = 2 * F2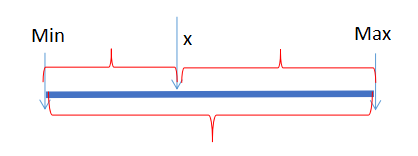

 

 n=4时，在F3的基础上，随便取一个数 y， F4 =F3 + max - y + y - min +| y - x | = F3 + F2 + | y - x | ,要想使F4最大，x、y需要分别为剩下数中最小值和最大值。         

 

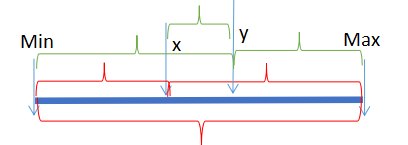
 排序，每次取最小或者最大，一定是最优的

（貌似看不懂别人的码）

 

遗漏：博弈论

http://t.csdn.cn/qTw77