51Nod 快速傅里叶变换题集选刷
打开51Nod全部问题页面,在右边题目分类中找到快速傅里叶变换,然后按分值排序,就是本文的题目顺序。
1.大数乘法问题
这个……板子就算了吧。
2.美妙的序列问题
长度为n的排列,且满足从中间任意位置划分为两个非空数列后,左边的最大值>右边的最小值。问这样的排列有多少个%998244353。
多组询问,n,T<=100000。
题解:经过分析可知,不合法的排列一定存在这样一种划分:
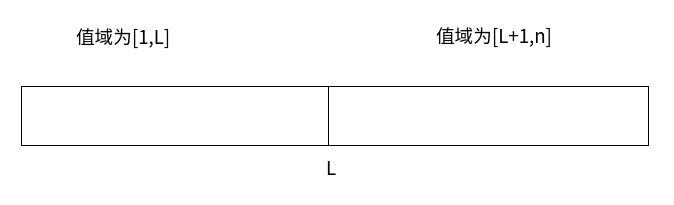
我们考虑答案=f[i]=i!-不合法排列个数。
形如 2 1 3 4 6 5 这种排列,会有三种划分方式不合法(1 | 3,3 | 4,4 | 6),直接算阶乘会计算重复。
而我们又发现,后两种划分,左边的子串仍是一个不合法的排列(显然)。
于是我们强制要求左边的排列是一个合法的排列,即在最左边统计贡献,这样就可以不重不漏了。
得到递推式显然:
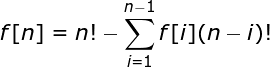
分治NTT即可,预处理后O(1)回答。

#include <iostream> #include <cstdio> #include <cstdlib> #include <algorithm> #include <cstring> #include <vector> #include <cmath> #include <map> #include <set> #define LL long long #define FILE "美妙的序列" using namespace std; const int N = 265010; const int Mod = 998244353; const int G = 3; int f[N],rev[N],L,Jc[N],a[N],b[N]; inline int gi(){ int x=0,res=1;char ch=getchar(); while(ch>'9' || ch<'0')res^=ch=='-',ch=getchar(); while(ch>='0'&&ch<='9')x=x*10+ch-48,ch=getchar(); return res?x:-x; } inline int QPow(int d,int z,int ans=1){ for(;z;z>>=1,d=1ll*d*d%Mod) if(z&1)ans=1ll*ans*d%Mod; return ans; } inline void NTT(int *A,int n,int f){ for(int i=1;i<n;++i) if(i<rev[i])swap(A[i],A[rev[i]]); for(int i=1;i<n;i<<=1){ int z=f*(Mod-1)/(i<<1),gn=QPow(G,(z+Mod-1)%(Mod-1)); for(int j=0;j<n;j+=i<<1){ int g=1,x,y; for(int k=0;k<i;++k,g=1ll*g*gn%Mod){ x=A[j+k];y=1ll*g*A[i+j+k]%Mod; A[j+k]=(x+y)%Mod;A[i+j+k]=(x-y+Mod)%Mod; } } } if(f==1)return;int iv=QPow(n,Mod-2); for(int i=0;i<n;++i)A[i]=1ll*A[i]*iv%Mod; } inline void solve(int l,int r){ if(l==r){f[l]=(Jc[l]-f[l]%Mod+Mod)%Mod;return;} int mid=(l+r)>>1; solve(l,mid); int n,m=r-l+1;L=0; for(n=1;n<=m;n<<=1)L++; for(int i=1;i<n;++i) rev[i]=(rev[i/2]/2)|((i&1)<<(L-1)); for(int i=0;i<n;++i)a[i]=b[i]=0; for(int i=l;i<=mid;++i)a[i-l]=f[i]; for(int i=0;i<m;++i)b[i]=Jc[i]; NTT(a,n,1);NTT(b,n,1); for(int i=0;i<n;++i)a[i]=1ll*a[i]*b[i]%Mod; NTT(a,n,-1); for(int i=mid+1;i<=r;++i)f[i]=(f[i]+a[i-l])%Mod; solve(mid+1,r); } int main(){ //freopen(FILE".in","r",stdin); //freopen(FILE".out","w",stdout); int Case=gi();Jc[0]=1; for(int i=1;i<=100000;++i) Jc[i]=1ll*Jc[i-1]*i%Mod; solve(1,100000); while(Case--)printf("%d\n",f[gi()]); fclose(stdin);fclose(stdout); return 0; }
3.哈希统计问题
给定base,p,求经过经典哈希(ans=(ans*base+a[i])%p;)后哈希值=x的长度<=n的小写字符串个数%998244353,n,p,base<=50000。
题解:对于长度<=n的问题先不考虑,先考虑恰好为n的。
设f[i][j]为已有i个字母,哈希值为j的串个数,则转移为: f[i][j] -> f[i+1][(j*base+Ascll[c])%p]。
如果把j*base看成模p意义下的j',显然转移是一个多项式相乘形式。
常见的套路是:观察当i为偶数时,f[i/2]是否能直接推出f[i]。
显然可以,j*base变成j*basei/2就可以了。写出来是一个卷积的形式,一遍NTT即可。
于是直接暴力递归,i为奇数则化为f[i-1]*f[1]继续暴力,只会做O(log)次。
现在要求<=n的,那么同样设pre[i][j]为已有<=i个字母,哈希值为j的串的个数。
转移:pre[i]*f[j]+pre[j] -> pre[i+j]。
即:选[j+1,i+j]个的和选[1,j]的方案数相加,就是选[1,i+j]个的个数。
剩下的就是一点细节,调试一会儿应该也很好写出来。

#include <iostream> #include <cstdio> #include <cstdlib> #include <algorithm> #include <cstring> #include <vector> #include <cmath> #include <map> #include <set> #define LL long long #define FILE "哈希统计" using namespace std; const int N = 265010; const int M = 60; const int Mod = 998244353; const int G = 3; int p,Bs,m,wx; int idf,idpre,f[M][N],pre[M][N],f_vis[N],pre_vis[N]; int n,rev[N],L,a[N],b[N]; inline int gi(){ int x=0,res=1;char ch=getchar(); while(ch>'9' || ch<'0')res^=ch=='-',ch=getchar(); while(ch>='0'&&ch<='9')x=x*10+ch-48,ch=getchar(); return res?x:-x; } inline int QPow(int d,int z,int Mod,int ans=1){ for(;z;z>>=1,d=1ll*d*d%Mod) if(z&1)ans=1ll*ans*d%Mod; return ans; } inline void NTT(int *A,int f){ for(int i=0;i<n;++i) if(i<rev[i])swap(A[i],A[rev[i]]); for(int i=1;i<n;i<<=1){ int z=f*(Mod-1)/(i<<1),gn=QPow(G,(z+Mod-1)%(Mod-1),Mod); for(int j=0;j<n;j+=i<<1){ int g=1,x,y; for(int k=0;k<i;++k,g=1ll*g*gn%Mod){ x=A[j+k];y=1ll*g*A[i+j+k]%Mod; A[j+k]=(x+y)%Mod;A[i+j+k]=(x-y+Mod)%Mod; } } } if(f==1)return;int iv=QPow(n,Mod-2,Mod); for(int i=0;i<n;++i)A[i]=1ll*A[i]*iv%Mod; } inline void Mul(int *H,int *g,int *h){ NTT(g,1);NTT(h,1); for(int i=0;i<n;++i) H[i]=1ll*g[i]*h[i]%Mod; NTT(H,-1); for(int i=n-1;i>=p;--i) H[i-p]=(H[i-p]+H[i])%Mod,H[i]=0; } inline int getf(int x){ if(f_vis[x])return f_vis[x]; if(x==1){ ++idf; for(int i='a';i<='z';++i) f[idf][i%p]++; return idf; } int id0,id1,len0,len1,pw; if(x&1)id0=getf(len0=x-1),id1=getf(len1=1); else id0=id1=getf(len0=len1=x/2); ++idf;pw=QPow(Bs,len1,p); for(int i=0;i<n;++i)a[i]=0,b[i]=f[id1][i]; for(int i=0;i<p;++i) if(f[id0][i]){ int y=1ll*i*pw%p; a[y]=(a[y]+f[id0][i])%Mod; } Mul(f[idf],a,b); return f_vis[x]=idf; } inline int getpre(int x){ if(pre_vis[x])return pre_vis[x]; if(x==1){ ++idpre;int id=getf(x); for(int i=0;i<n;++i) pre[idpre][i]=f[id][i]; return idpre; } int id0,id1,id2,len0,len1,pw; if(x&1)id0=getpre(len0=x-1),id1=getf(len1=1); else id0=getpre(len0=x/2),id1=getf(len1=x/2); id2=getpre(len1);pw=QPow(Bs,len1,p);++idpre; for(int i=0;i<n;++i)a[i]=0,b[i]=f[id1][i]; for(int i=0;i<p;++i) if(pre[id0][i]){ int y=1ll*i*pw%p; a[y]=(a[y]+pre[id0][i])%Mod; } Mul(pre[idpre],a,b); for(int i=0;i<p;++i) pre[idpre][i]=(pre[idpre][i]+pre[id2][i])%Mod; return pre_vis[x]=idpre; } int main(){ //freopen(FILE".in","r",stdin); //freopen(FILE".out","w",stdout); m=gi();Bs=gi();p=gi();wx=gi(); for(n=1;n<p+p;n<<=1)L++; for(int i=0;i<n;++i) rev[i]=(rev[i/2]/2)|((i&1)<<(L-1)); int id=getpre(m); printf("%d\n",pre[id][wx]); fclose(stdin);fclose(stdout); return 0; }
4.乘积之和
给定正整数序列序列A[1...n],有Q次询问,每次询问给出k,在A中任选k个数可以得到一个乘积。求所有方案的乘积的总和%100003。n,Q<=50000。
题解:暴力DP很显然,设f[i][j]表示前i个数选j个数的乘积和,那么可以直接转移f[i][j] -> f[i+1][j*A[i+1]%100003]。
用上面那题的套路,f[i/2]是否能推出f[i]?仔细分析后发现是可以的。
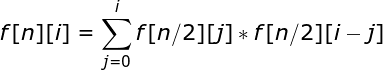
发现这也是一个卷积形式!但是这题是有多组询问的,不能直接暴力递归求。
分治•NTT,solve(l,r)表示得到在A[l...r]中选k个的乘积和数组,总复杂度O(nlog2n),最后求出所有解。
因为不是费马质数,卷积上界又只有10^14级别,两个费马质数用中国剩余定理合并一下就可以了。
upd:用母函数来理解可能更好。
易推出我们求的是多项式

在xk项的系数。同样的,上式可用分治法,合并时使用NTT,代码是一样的。

#include <iostream> #include <cstdio> #include <cstdlib> #include <algorithm> #include <cstring> #include <vector> #include <cmath> #include <map> #include <set> #define LL long long #define FILE "乘积之和" using namespace std; const LL N = 200010; const LL M = 100003; const LL G = 3; LL Q,A[N]; LL f[20][N],rev[N]; LL P[]={998244353,1004535809}; inline LL gi(){ LL x=0,res=1;char ch=getchar(); while(ch>'9' || ch<'0')res^=ch=='-',ch=getchar(); while(ch>='0'&&ch<='9')x=x*10+ch-48,ch=getchar(); return res?x:-x; } inline LL Mul(LL a,LL b,LL Mod,LL ans=0){ if(Mod<=P[1])return a*b%Mod; for(;b;b>>=1,a=(a+a)%Mod) if(b&1)ans=(ans+a)%Mod; return ans; } inline LL QPow(LL d,LL z,LL Mod,LL ans=1){ for(d=d%Mod,z=z%Mod;z;z>>=1,d=d*d%Mod) if(z&1)ans=ans*d%Mod; return ans; } inline void NTT(LL *A,LL n,LL f,LL Mod){ for(LL i=0;i<n;++i) if(i<rev[i])swap(A[i],A[rev[i]]); for(LL i=1;i<n;i<<=1){ LL z=f*(Mod-1)/(i<<1),gn=QPow(G,(z+Mod-1)%(Mod-1),Mod); for(LL j=0;j<n;j+=i<<1){ LL g=1,x,y; for(LL k=0;k<i;k++,g=1ll*g*gn%Mod){ x=A[j+k];y=1ll*g*A[i+j+k]%Mod; A[j+k]=(x+y)%Mod;A[i+j+k]=(x-y+Mod)%Mod; } } } if(f==1)return;LL iv=QPow(n,Mod-2,Mod); for(LL i=0;i<n;++i)A[i]=1ll*A[i]*iv%Mod; } inline LL CRT(LL r0,LL r1){ LL Mod=1ll*P[0]*P[1]; LL v0=QPow(P[1],P[0]-2,P[0]),v1=QPow(P[0],P[1]-2,P[1]); LL r=(Mul(v0*P[1]%Mod,r0,Mod)+Mul(v1*P[0]%Mod,r1,Mod))%Mod; return r%M; } inline void solve(LL l,LL r,LL dep){ if(l==r){ f[dep][0]=1;f[dep][1]=A[l]%M; return; } LL mid=(l+r)>>1; LL m=r-l+1,n=1,L=0; for(;n<=m;n<<=1)L++; LL a[2][n+10],b[2][n+10]; solve(l,mid,dep+1); for(LL i=0;i<=mid-l+1;++i)a[0][i]=a[1][i]=f[dep+1][i]; for(LL i=mid-l+2;i<n;++i)a[0][i]=a[1][i]=0; solve(mid+1,r,dep+1); for(LL i=0;i<=r-mid;++i)b[0][i]=b[1][i]=f[dep+1][i]; for(LL i=r-mid+1;i<n;++i)b[0][i]=b[1][i]=0; for(LL i=0;i<n;++i) rev[i]=(rev[i/2]/2)|((i&1)<<(L-1)); for(LL t=0;t<2;++t){ NTT(a[t],n,1,P[t]);NTT(b[t],n,1,P[t]); for(LL i=0;i<n;++i)a[t][i]=1ll*a[t][i]*b[t][i]%P[t]; NTT(a[t],n,-1,P[t]); } for(LL i=0;i<=m;++i) f[dep][i]=CRT(a[0][i],a[1][i]); } int main(){ LL n=gi();Q=gi(); for(LL i=1;i<=n;++i)A[i]=gi(); solve(1,n,1); for(LL t=1;t<=Q;++t) printf("%lld\n",f[1][gi()]); fclose(stdin);fclose(stdout); return 0; }
5.模糊搜索问题
题意:给定两个串A,B,字符集大小为4,匹配规则是若A[j-k]~A[j+k]中存在B[i]则算B[i]在A[j]出现,求B在A中出现了多少次,长度<=100000。
比如说k=2的情况。
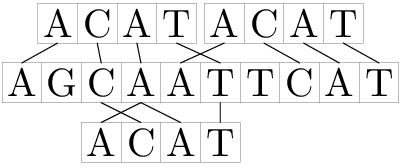
题解:这种字符串问题用FFT来做的套路似乎都和万径人踪灭差不多?
首先那个k的限制可以用两遍扫+差分搞定出字符c在A[i]出是否算的上出现,记为g[c][i]。
B在A[i]处开头,则对于'A'、'T'、'C'、‘G’,,有如下式子:
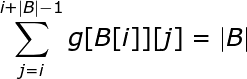
这样仍不好做,把式子构造一下:
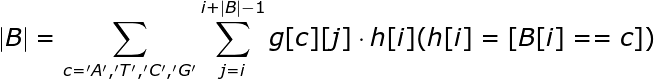
这就形成了多项式乘法的形式,跑四遍就可以了。

#include <iostream> #include <cstdio> #include <cstdlib> #include <algorithm> #include <cstring> #include <vector> #include <cmath> #include <map> #include <set> #define LL long long #define FILE "模糊搜索" using namespace std; const int N = 530010; const double pi = acos(-1.0); int S,T,K,n,m,L,rev[N],ID[99],cf[N],num[5][N],Ans; struct dob{ double real,imag; dob(){}; dob(double _r,double _i){real=_r;imag=_i;} dob operator +(const dob &a)const{ return (dob){real+a.real,imag+a.imag}; } dob operator -(const dob &a)const{ return (dob){real-a.real,imag-a.imag}; } dob operator *(const dob &a)const{ double r=real*a.real-imag*a.imag; double i=real*a.imag+imag*a.real; return (dob){r,i}; } }a[N],b[N],f[5][N]; char s[N],t[N]; inline int gi(){ int x=0,res=1;char ch=getchar(); while(ch>'9'||ch<'0'){if(ch=='-')res*=-1;ch=getchar();} while(ch<='9'&&ch>='0')x=x*10+ch-48,ch=getchar(); return x*res; } inline void FFT(dob *A,int f){ for(int i=0;i<n;++i) if(i<rev[i])swap(A[i],A[rev[i]]); for(int i=1;i<n;i<<=1){ dob wn(cos(pi/i),sin(f*pi/i)),x,y; for(int j=0;j<n;j+=i<<1){ dob w(1,0); for(int k=0;k<i;k++,w=w*wn){ x=A[j+k];y=w*A[i+j+k]; A[j+k]=x+y;A[i+j+k]=x-y; } } } if(f==1)return; for(int i=0;i<n;++i) A[i].real=int(A[i].real/n+0.5); } inline void work(char ch,int sum=0){ for(int i=0;i<n;++i)cf[i]=0; for(int i=1;i<=S;++i) if(s[i]==ch){ cf[max(0,i-K)]++; cf[min(n+1,i+K+1)]--; } for(int i=1;i<n;++i)cf[i]+=cf[i-1]; for(int i=0;i<=S;++i) a[i].real=cf[i]>0,a[i].imag=0; for(int i=S+1;i<n;++i) a[i].real=a[i].imag=0; for(int i=0;i<=T;++i) sum+=b[i].real=t[i]==ch,b[i].imag=0; for(int i=T+1;i<n;++i) b[i].real=b[i].imag=0; reverse(b+1,b+T+1); FFT(a,1);FFT(b,1); for(int i=0,id=ID[ch];i<n;++i) f[id][i]=a[i]*b[i]; FFT(f[ID[ch]],-1); for(int i=1;i<=S;++i) num[ID[ch]][i]=sum==int(f[ID[ch]][i+T].real+0.001); } int main(){ //freopen(FILE".in","r",stdin); //freopen(FILE".out","w",stdout); S=gi();T=gi();K=gi(); for(n=1,m=S+T;n<m;n<<=1)L++; for(int i=1;i<n;++i) rev[i]=(rev[i/2]/2)|((i&1)<<(L-1)); ID['A']=1;ID['T']=2;ID['C']=3;ID['G']=4; scanf("%s%s",s+1,t+1); work('A');work('T');work('C');work('G'); for(int i=1;i<=S;++i) if(num[1][i] && num[2][i] && num[3][i] && num[4][i]) Ans++; printf("%d\n",Ans); fclose(stdin);fclose(stdout); return 0; }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号