BZOJ3571 HNOI2014 画框

3571: [Hnoi2014]画框

Time Limit: 20 Sec  Memory Limit: 128 MB

Description

小T准备在家里摆放几幅画，为此他买来了N幅画和N个画框。为了体现他的品味，小T希望能合理地搭配画与画框，使得其显得既不过于平庸也不太违和。对于第 幅画与第 个画框的配对，小T都给出了这个配对的平凡度Aij 与违和度Bij 。整个搭配方案的总体不和谐度为每对画与画框平凡度之和与每对画与画框违和度的乘积。具体来说，设搭配方案中第i幅画与第Pi个画框配对，则总体不和谐度为

 

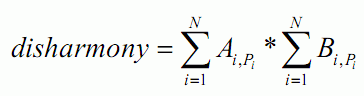
小T希望知道通过搭配能得到的最小的总体不和谐度是多少。

Input

输入文件第 行是一个正整数T ，表示数据组数，接下来是T组数据。
对于每组数据，第 行是一个正整数N，表示有N对画和画框。
第2到第N+1行，每行有N个非负整数，第i+1 行第j个数表示Aij 。
第N+2到第2*N+1行，每行有N个非负整数，第i+N+1 行第j个数表示Bij 。

Output

包含T行，每行一个整数，表示最小的总体不和谐度

Sample Input

1
3
4 3 2
2 3 4
3 2 1
2 3 2
2 2 4
1 1 3

Sample Output

30

HINT

第1幅画搭配第3个画框，第2幅画搭配第1个画框，第3 幅画搭配第2个画框，则总体不和谐度为30

 

　　因为我不会最小乘积生成树这种鬼东西，所以没看出来，所以又去看了题解。

　　暑假CLJ老师大概讲了一下思路，然后我发现这个东西很有意思。思路大致是这样的：

　　把方案看成二位平面上的点，(x,y)表示(sum(A),sum(B))。

　　则把这些点画出来之后，可以画一条反比例函数，让k越来越小，找到答案。

　　这样做似乎是不可行的，但是反比例函数的图像可以给我们启示：

　　　　答案一定在下凸包内，在左下角内。

　　直接建图找凸包也是不可行的，因为这一类题的点数一般是nⁿ这种数。

　　那么左下凸包有什么性质呢：

　　　　最左边，最下面的点一定在凸包上。

　　记上面两个点为A(xa,ya),B(xb,yb)：

　　　　对于所有在左下凸包上的点K，cross(BA,BK)>=0.

　　　　离AB最远的点T(S_△ABT最大,cross最大)一定在左下凸包上。

　　　　当A,B,T三点共线(cross=0)的时候，就没必要再找了，因为答案在A,B出一定有比T处更优秀。

　　这样一来，就可以递归分治处理。

　　那么如何找到这个T呢？

　　∵Cross(BA,BT)max

　　∴Cross(BA,BT)怎么算呢？

　(C为常数)

 

　　于是只要最大化前面那个东西就好了。

　　然后按照上面所说的连边方式，进行二分图最大权匹配。

　　不会写KM只会写费用流。

　　所以只能在BZOJ上面交。

#include    <iostream>
#include    <cstdio>
#include    <cstdlib>
#include    <algorithm>
#include    <vector>
#include    <cstring>
#include    <queue>
#include    <complex>
#include    <stack>
#define LL long long int
#define dob double
using namespace std;
 
const int N = 151;
const int Inf = 2147483641;
struct Node{int to,C,val,facx,facy,next;}E[N*N*2];
struct Point{int x,y;};
int n,A[N][N],B[N][N],head[N],tot,far[N],in[N],up[N],Ans,S,T;
 
inline int gi(){
  int x=0,res=1;char ch=getchar();
  while(ch>'9'||ch<'0'){if(ch=='-')res*=-1;ch=getchar();}
  while(ch<='9'&&ch>='0')x=x*10+ch-48,ch=getchar();
  return x*res;
}
 
inline int Cross(Point a,Point b,Point c){
  return (b.x-a.x)*(c.y-a.y)-(b.y-a.y)*(c.x-a.x);
}
 
inline void link(int u,int v,int c,int val,int fca,int fcb){
  E[++tot]=(Node){v,c,val,fca,fcb,head[u]};
  head[u]=tot;
  E[++tot]=(Node){u,0,-val,-fca,-fcb,head[v]};
  head[v]=tot;
}
 
inline bool SPFA(Point &ans){
  memset(far,127/3,sizeof(far));
  memset(up,0,sizeof(up));
  queue<int>Q;Q.push(S);far[S]=0;
  int fx=0,fy=0;
  while(!Q.empty()){
    int x=Q.front();Q.pop();in[x]=0;
    for(int e=head[x];e;e=E[e].next){
      int y=E[e].to;
      if(E[e].C<=0 || far[x]+E[e].val>=far[y])
        continue;
      far[y]=far[x]+E[e].val,up[y]=e;
      if(!in[y])Q.push(y),in[y]=1;
    }
  }
  if(!up[T])return false;
  for(int i=T;i!=S;i=E[up[i]^1].to){
    fx+=E[up[i]].facx,fy+=E[up[i]].facy;
    E[up[i]].C--;E[up[i]^1].C++;
  }
  ans.x+=fx;ans.y+=fy;return true;
}
 
inline Point fyl(){
  Point ans=(Point){0,0};
  while(SPFA(ans));
  Ans=min(Ans,ans.x*ans.y);
  return ans;
}
 
inline Point getp(int xv,int yv){
  memset(head,0,sizeof(head));tot=1;
  for(int i=1;i<=n;++i){
    link(S,i,1,0,0,0);
    for(int j=1;j<=n;++j)
      link(i,j+n,1,xv*A[i][j]+yv*B[i][j],A[i][j],B[i][j]);
    link(i+n,T,1,0,0,0);
  }
  return fyl();
}
 
inline void solve(Point Pa,Point Pb){
  Point mid=getp(Pa.y-Pb.y,Pb.x-Pa.x);
  if(Cross(Pb,Pa,mid)>0)
    solve(Pa,mid),solve(mid,Pb);
}
 
int main()
{
  /*freopen(".in","r",stdin);
    freopen(".out","w",stdout);*/
  int Case=gi();
  while(Case--){
    n=gi();Ans=Inf;S=0;T=2*n+1;
    for(int i=1;i<=n;++i)
      for(int j=1;j<=n;++j)
        A[i][j]=gi();
    for(int i=1;i<=n;++i)
      for(int j=1;j<=n;++j)
        B[i][j]=gi();
    if(n==1){
      printf("%d\n",A[1][1]*B[1][1]);
      continue;
    }
    Point Pa=getp(1,0),Pb=getp(0,1);
    solve(Pa,Pb);
    printf("%d\n",Ans);
  }
  /*fclose(stdin);
    fclose(stdout);*/
  return 0;
}