深度学习6一般线性模型
在前面我们曾经有一个问题,就是在logistic回归中,我们为什么用
对于这个问题,我们先定义了一个一般线性模型
这个分布也就是指数分布
伯努利分布,高斯分布,泊松分布,贝塔分布,狄特里特分布都可以用这个指数分布来表示。
在对数回归时采用的是伯努利分布,对于伯努利分布,可以表示成
则我们对照上面的一般线性模型
则对照上面的一般线性模型。有
这个也就是我们前面的线性回归。
好的,下面总结一下思路:
1. 对于我们要估计的值,我们就将其转化到某个分布中去,(特定的问题转化到特定的分布)
比如分类问题,我们只有0跟1,则我们转换到0,1分布中去,则我们就用到一个函数![clip_image002[1] clip_image002[1]](http://images0.cnblogs.com/blog/311205/201305/19001853-ac0ba0b212654f48b4391aa34caf7d82.gif)
2.对于其他的问题,也就可以转化到其他分布上去。对于可以转化的问题就是给点x和θ,分布y服从以η为参数一般线性模型。![]()
3.我们的目标是在x的条件下预测真实值![]() ,
,![]() 一般情况为y,对于我们的预测函数h(x),认为其实在x条件下y的期望,
一般情况为y,对于我们的预测函数h(x),认为其实在x条件下y的期望,![]() ,则
,则
这样对于前面的logistic回归的理论就有了。





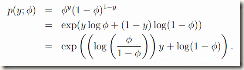

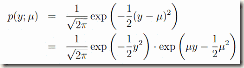
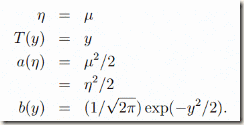

 浙公网安备 33010602011771号
浙公网安备 33010602011771号