第7章：LeetCode--算法：递归问题

70. Climbing Stairs

This problem is a Fibonacci problem.
F(n)=F(n-1)+F(n-2);
Solving this problem by recursion ,we will do a lot of same recursion.
Example:
F(10)=F(9)+F(8);
F(9)=F(8)+F(7);
we calculate F(8) twice,when n is large,this will increase as a rate of n's exponent.

So a more efficient way to solve this problem is from Bottom to Top.
Calculate F(0) ,F(1);
then F(2).........

//F(n) = F(n-1) + F(n-2)
class Solution {
public:
    int climbStairs(int n) {
        //if(n<=2) return n; //0,1
        int f0 = 0, f1=1, steps =0;
        for(int i=0; i<n; i++){
            steps = f0+f1;
            f0 = f1;
            f1 = steps;
        }
        return steps;
    }
};

//Recursion time out
/*class Solution {
public:
    int climbStairs(int n) {
        if(n<=2) return n; //0,1
        int steps = 0;
        steps += climbStairs(n-1);
        steps += climbStairs(n-2);
        return steps;
    }
};*/

 

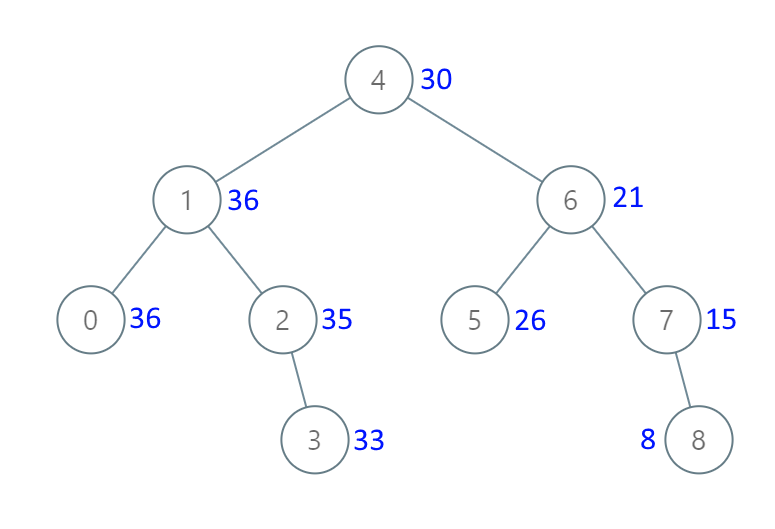
LeetCode -- 1038. Binary Search Tree to Greater Sum Tree　

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int preroot = 0;
    TreeNode* bstToGst(TreeNode* root) {
        if(root->right)
            bstToGst(root->right);
        preroot = root->val = root->val + preroot;
        if(root->left)
            bstToGst(root->left);
        return root;
    }
};