子集系列(一) 传统subset 问题，例 [LeetCode] Subset, Subset II, Bloomberg 的一道面试题

引言

Coding 问题中有时会出现这样的问题：给定一个集合，求出这个集合所有的子集(所谓子集，就是包含原集合中的一部分元素的集合)。

或者求出满足一定要求的子集，比如子集中元素总和为定值，子集元素个数为定值等等。

我把它们归类为子集系列问题。

这篇博文作为子集系列第一篇，着重讨论最传统的子集问题，也就是“给定一个集合，求出这个集合所有的子集”，没有附加要求。我会讨论解决此类题目的两种思路，并做一些比较。

还是从具体题目开始

例题1, 不包含重复元素的集合S，求其所有子集

Given a set of distinct integers, S, return all possible subsets.

Note:

Elements in a subset must be in non-descending order.
The solution set must not contain duplicate subsets.

For example,
If S = [1,2,3], a solution is:

[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

class Solution {
public:
    vector<vector<int> > subsets(vector<int> &S) {
    }
};

题目来自LeetCode Subsets

思路一

可以用递推的思想，观察S=[], S =[1], S = [1, 2] 时解的变化。

可以发现S=[1, 2] 的解就是把S = [1]的所有解末尾添上2，然后再并上S = [1]里面的原有解。因此可以定义vector<vector<int> > 作为返回结果res, 开始时res里什么都没有，第一步放入一个空的vecotr<int>，然后这样迭代n次，每次更新res 内容，最后返回res。

代码：

class Solution {
public:
    vector<vector<int> > subsets(vector<int> &S) {
        vector<vector<int> > res;
        vector<int> emp;
        res.push_back(emp);
        sort(S.begin(), S.end());
        if(S.size() == 0) return res;
        for(vector<int>::iterator ind = S.begin(); ind < S.end(); ++ind){
            int size = res.size();
            for(int i = 0; i < size; ++i){
                vector<int> v;
                for(vector<int>::iterator j = res[i].begin(); j < res[i].end(); ++j){
                   v.push_back(*j);
                }
                v.push_back(*ind);
                res.push_back(v);
            }
        }
        return res;
    }
};

10 / 10 test cases passed. Runtime: 16 ms

这里注意因为res一直在增长，所以遍历res的时候不能用vector<int>::iterator，否则可能因为vector重新allocate内存而地址失效，因此直接使用数组下标。

思路二

所谓子集，就是包含原集合中的一些元素，不包含另一些元素。如果单独看某一个元素，它都有两种选择："被包含在子集中"和"不被包含在子集中"，对于元素个数为n、且不含重复元素的S，子集总数是2ⁿ。因此我们可以遍历S的所有元素，然后用递归考虑每一个元素包含和不包含的两种情况。

代码，这种思路需要用到递归

class Solution {
public:
    vector<vector<int> > subsets(vector<int> &S) {
        vector<int> v;
        sort(S.begin(), S.end());
        subsetsCore(S, 0, v);
        return res;
    }
private:
    vector<vector<int> > res;
    void subsetsCore(vector<int> &S, int start, vector<int> &v){
        if(start == S.size()) { res.push_back(v); return;}
        vector<int> v2;
        for(vector<int>::iterator i = v.begin(); i < v.end(); v2.push_back(*(i++)));
        v.push_back(S[start]);
        subsetsCore(S, start+1, v); //包含S[start]
        subsetsCore(S, start+1, v2); //不包含S[start]
    }
};

10 / 10 test cases passed. Runtime: 40 ms

例题2，S中包含有重复元素

原题中规定原集合S中的元素是distinct的。如果S中包含有重复元素(也就是LeetCode中题Subset II)，这种思路需要如何改进？

Subsets II

Given a collection of integers that might contain duplicates, S, return all possible subsets.

Note:

Elements in a subset must be in non-descending order.
The solution set must not contain duplicate subsets.

思路一

我们以S=[1,2,2]为例:

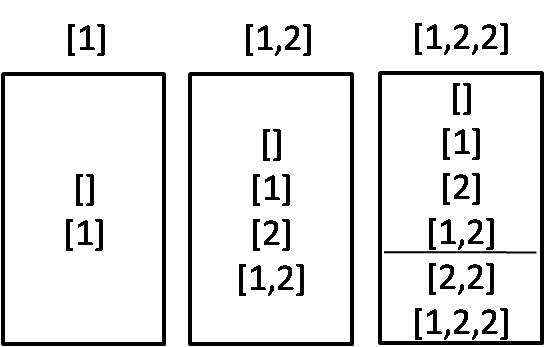
可以发现从S=[1,2]变化到S=[1,2,2]时，多出来的有两个子集[2,2]和[1,2,2]，这两个子集，其实就是 [2], [1,2]末尾都加上2 而产生。而[2], [1,2] 这两个子集实际上是 S=[1,2]的解到 S=[1]的解新添加的部分。

因此，若S中有重复元素，可以先排序；遍历过程中如果发现当前元素S[i] 和 S[i-1] 相同，那么不同于原有思路中“将当前res中所有自己拷贝一份再在末尾添加S[i]”的做法，我们只将res中上一次添加进来的子集拷贝一份，末尾添加S[i]。

代码：

class Solution {
public:
    vector<vector<int> > subsetsWithDup(vector<int> &S) {
        vector<vector<int> > subsets;
        vector<int> v;
        subsets.push_back(v);
        if(S.empty()) return subsets;
        sort(S.begin(), S.end());
        int m = 0; //m 用来存储上一次加进来的子集们的起始index
        for(vector<int>::iterator i = S.begin(); i < S.end(); ++i){
            int start = ((i != S.begin() && *i == *(i-1)) ? m : 0); //如果S的当前元素和前一个元素相同，只拷贝上次加进来的子集
            int end = subsets.size();
            for(int j = start; j < end; ++j){
                vector<int> vt;
                for(vector<int>::iterator k = subsets[j].begin(); k < subsets[j].end(); ++k){
                    vt.push_back(*k);
                }
                vt.push_back(*i);
                subsets.push_back(vt);
            }
            m = end;
        }
        return subsets;
    }
};

19 / 19 test cases passed，Runtime: 72 ms

小结：

思路一的切入点是：比较S=[1]和S=[1,2] 的解的区别，找到转移方程。实现方式是不停迭代和更新res。

实现的优势是不需要使用递归，迭代即可完成；但需要定义一个vector<vector<int> > res，然后迭代过程中不停基于res已有的子集生成新的子集，再添加到res中，也就是说res除了用于最终返回，在迭代过程中还有临时存放点的作用。

用与上题类似的思路二来解：

对于含有重复元素的S，可以先排序，然后考虑去重：我们可以发现如果所遍历的当前元素S[i] 和目前的子集的末尾元素相同，那么就不再需要考虑"不包含当前元素到子集中"的情况，只需要考虑"包含当前元素到子集中一种情况"。举个例子：对于S=[1,2,2]，如果遍历到第二个"2"，当前子集v是[1, 2]，这个时候如果考虑"不把2包含进子集的情况"，即维持子集=[1,2]不动，遍历下一个元素；这样其结果会出现重复。因为考虑另一个递归调用，其当前子集v是[1]，也遍历到了S的第二个"2"，它将这个"2"元素放入当前子集，虽然继续遍历下一个元素。这两个递归调用的结果是重复的。因此，若当前递归调用所遍历到的元素和当前子集v的末尾元素相同，只考虑"把当前元素添加到子集末尾"的情况。

代码

class Solution {
public:
    vector<vector<int> > subsetsWithDup(vector<int> &S) {
        vector<int> v;
        sort(S.begin(), S.end());
        subsetsCore(S, 0, v);
        return res;
    }
private:
    vector<vector<int> > res;
    void subsetsCore(vector<int> &S, int start, vector<int> &v){
        if(start == S.size()) { res.push_back(v); return;}
        if(v.size() == 0 || v[v.size()-1] != S[start]){    //When S[start] != v[v.size()-1], we need to consider both case: add S[start] into v; not add S[start] to v. If S[start] == v[v.size()-1], we only need to consider the case add S[start] into v.
            vector<int> v2;
            for(vector<int>::iterator i = v.begin(); i < v.end(); v2.push_back(*(i++)));
            subsetsCore(S, start+1, v2);
        }
        v.push_back(S[start]);
        subsetsCore(S, start+1, v);
    }
};

19 / 19 test cases passed，Runtime: 52 ms

上面的解法中因为老是要从v拷贝元素到v2，所以比较占用时间，可以设置一个全局vector<int>，回溯增删。

class Solution {
public:
    vector<vector<int> > subsetsWithDup(vector<int> &S) {
        sort(S.begin(), S.end());
        subsetsCore(S, 0);
        return res;
    }
private:
    vector<int> path;
    vector<vector<int> > res;
    void subsetsCore(vector<int> &S, int start){
        if(start == S.size()) { res.push_back(path); return;}
        if(path.size() == 0 || path[path.size()-1] != S[start])
            subsetsCore(S, start+1);    //When S[start] != v[v.size()-1], we need to consider both case: add S[start] into v; not add S[start] to v. If S[start] == v[v.size()-1], we only need to consider the case add S[start] into v.
        path.push_back(S[start]);
        subsetsCore(S, start+1);
        path.pop_back();
    }
};

19 / 19 test cases passed，Runtime: 48 ms

因为case区分度不够的缘故，在这个例子中没有快太多，但在下一篇文章中的Combination 例题中，使用全局的path会省去很多时间。

小结

从本质上来说，思路二和思路一是同一种解法，只是切入角度不同，致使实现方式不同。思路二虽然没有显示定义vector<vector<int>>来存放所有子集，但是所有递归里新开的vector<int>，加起来所占用的空间和思路一所占用空间一样，思路二还多出了递归所占用的栈空间。

例题3，string 的子集

子集求解可以再做一些改变，比如：S不再是一个vector<int>，而是一个string，求其所有的sub string。

我参加Bloomberg的面试时，曾经遇到S为string的题目，S的长度小于30，要求求出S这个字符串所有的sub string。例如S = "abc"，输出 "a" "b" "c" "ab" "ac" "bc" "abc"，空子串不需要输出。

要求不能用递归，不能申请vector或者数组，直接输出所有sub string。当时我曾经做过LeetCode上的Subset，也就是本文中拿来当例题的题目，刷LeetCode时，用第一种思路解出来了，就没有再继续深究下去。结果遇到这一题时(只有十多分钟解题)，一紧张，满脑子都是原来的思路一，没能给出符合要求的解。

其实如果从"每个元素都有包含进子集和不包含进子集两种可能"，也就是思路二入手，这个问题就可以解决。

思路二的本质是"考虑每一个元素的两种情况"，虽然不能用递归，但是因为S的长度小于30，我们可以用一个unsigned int 的每个bit位来表示S的每一个字符的两种情况。当然这解法的前提是S这个string中不含重复字符。

代码

void subsets(string s) {
    if(s.length() == 0) return;
    unsigned int i = 1, judgeEnd = (1 << s.length()) - 1; //judgeEnd用来判定i 递增的终止
    unsigned int mask = 0; //mask用于滤出 i 的每一位
    int j = 0;
    for(; (i & judgeEnd) > 0; cout << endl, ++i){
        for(mask = 1 << (s.length() - 1), j = 0; j < s.length(); ++j, mask = mask >> 1){
            if(mask & i) cout << s[j];
        }
    }
}

做过类似的题目依然面试没过，也算是一个惨痛的教训吧。刷题的本质，是为了让自己通过接触不同的题目，在总结思考中提升coding能力。对于做的每一题，都需要发散开来，探究不同的解法和思路；如果仅仅满足于AC，结果一旦题目有所变化，反而会被原来的思路束缚住手脚。

续篇：

子集系列(二) 满足特定要求的子集

posted on 2014-06-08 07:36 Felix Fang 阅读(11362) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

Felix 的博客