[概率论与数理统计]笔记：3.2 条件分布与随机变量的独立性

3.2 条件分布与随机变量的独立性

条件分布

• 分布函数：\(F(x)=P\{X\le x\}\)
• 条件分布函数：\(F(x|A)=P\{X\le x|A\}\)

条件分布：事件\(A\)发生的条件下，\(X\)的分布函数就叫条件分布函数。( 事件\(A\)会对事件\(\{X\le x\}\)发生的概率产生影响。)

离散型条件分布

假设有两个随机变量\(X,Y\)，在\(Y=y_j\)的条件下，要求\(X\)的分布，即\(P\{X\le x|Y=y_j\}\)。

解题思路：

1. 画出联合概率分布表，计算边缘概率，其中\(P\{Y=y_j\}=\sum\limits_ip_{ij}\)。
2. \(P\{X=x_i|Y=y_j\}=\frac{P\{X=x_i,Y=y_j\}}{P\{Y=y_j\}}\)

连续型条件分布

• 随机向量\((X,Y)\)
• 密度函数\(f(x,y)\)
• 边缘密度函数\(f_X(x),f_Y(y)\)

若\(f_Y(y)>0\)，在\(Y=y\)的条件下，条件分布函数

\[F(x|y)=\int_{-\infty}^x\frac{f(u,y)}{f_Y(y)}\mathrm{d}u \]

而条件密度函数

\[f(x|y)=\frac{f(x,y)}{f_Y(y)} \]

同理，在\(X=x\)的条件下，

\[F(y|x)=\int_{-\infty}^y\frac{f(x,v)}{f_X(x)}\mathrm{d}v \]

\[f(y|x)=\frac{f(x,y)}{f_X(x)} \]

这里简单的证明一下第一个公式：

\[F(x|y)=P\{X\le x|Y=y\}=\frac{P\{X\le x,Y=y\}}{P\{Y=y\}} \]

这里的分子分母均为0。

类似于可以将\(x=5\)表示为\(\lim\limits_{\varepsilon\to0}5\le x\le5+\varepsilon\)，

这里将上式表示为下式：

\[\begin{align*} 原式 &= \lim\limits_{\varepsilon\to0}\frac{P\{X\le x,y\le Y\le y+\varepsilon\}}{P\{y\le Y\le y+\varepsilon\}}\\ &= \lim\limits_{\varepsilon\to0}\frac{\int_{-\infty}^x\int_y^{y+\varepsilon}f(u,v)\mathrm{d}v\mathrm{d}u}{\int_y^{y+\varepsilon}f_Y(v)\mathrm{d}v} \\ &= \lim\limits_{\varepsilon\to0}\frac{\int_{-\infty}^x\frac{1}{\varepsilon}\int_y^{y+\varepsilon}f(u,v)\mathrm{d}v\mathrm{d}u}{\frac{1}{\varepsilon}\int_y^{y+\varepsilon}f_Y(v)\mathrm{d}v} \end{align*} \]

积分中值定理：存在\(\xi\in[a,b]\)使得\(\int_a^bf(x)\mathrm{d}x=f(\xi)(b-a)\)

详细表述👉积分中值定理_百度百科 (baidu.com)

根据积分中值定理，分母的\(\varepsilon\)为区间长度，则存在\(\xi\in[y,y+\varepsilon]\)使得\(\frac{1}{\varepsilon}\int_y^{y+\varepsilon}f_Y(v)dv=f_Y(\xi)\).

又因为\(y\le\xi\le y+\varepsilon\)且\(\varepsilon\to0\)，所以\(\xi=y\).

所以\(\frac{1}{\varepsilon}\int_y^{y+\varepsilon}f_Y(v)dv=f_Y(y)\)

分子部分同理，根据积分中值定理，分子部分中间的\(\frac{1}{\varepsilon}\int_y^{y+\varepsilon}f(u,v)\mathrm{d}v=f(u,y)\)

因此，原式\(=\frac{\int_{-\infty}^xf(u,y)\mathrm{d}u}{f_Y(y)}\)（这里的分母是常数，可以移到积分内部）

综上，

\[F(x|y)=\int_{-\infty}^x\frac{f(u,y)}{f_Y(y)}\mathrm{d}u \]

总结：

1. 将点转换为长度趋于0的区间。
2. 积分中值定理。

---

随机变量的独立性

定义

如果\(X,Y\)满足

\[f(x|y)=f_X(x)=\frac{f(x,y)}{f_Y(y)} \]

即

\[f(x,y)=f_X(x)f_Y(y) \]

则说\(X,Y\)是相互独立的。

同理有\(F(x,y)=F_X(x)F_Y(y)\)。

充要条件

\(X,Y\)相互独立的充要条件是\(X\)的所有事件与\(Y\)的所有事件独立：

\[P\{X\in S_x,Y\in S_y\}=P\{X\in S_x\}P\{Y\in S_y\} \]

二维离散型的独立性

如果联合概率等于边缘概率的乘积，则相互独立。

\[P\{X=x_i,Y=y_j\}=P\{X=x_i\}P\{Y=y_j\} \]

这里的\(i,j\)需要遍历所有情况，

• 只要有一个不等于，就不满足相互独立。
• 如果对于所有的\(i,j\)都相等，则相互独立。

图解：

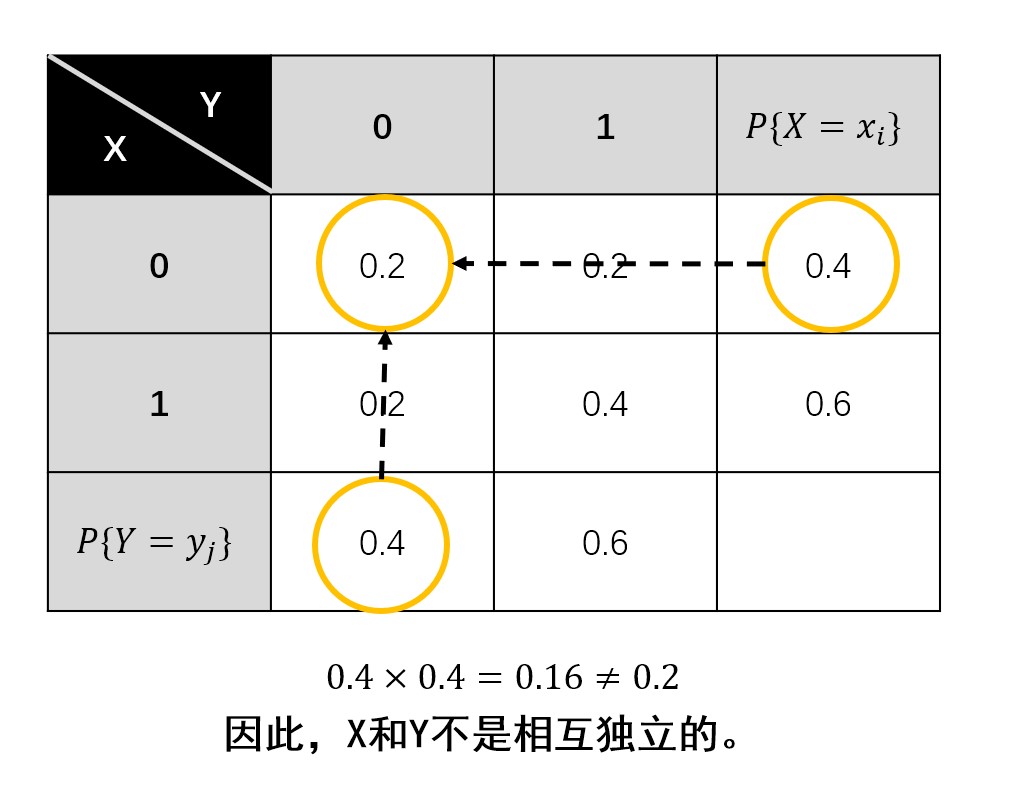
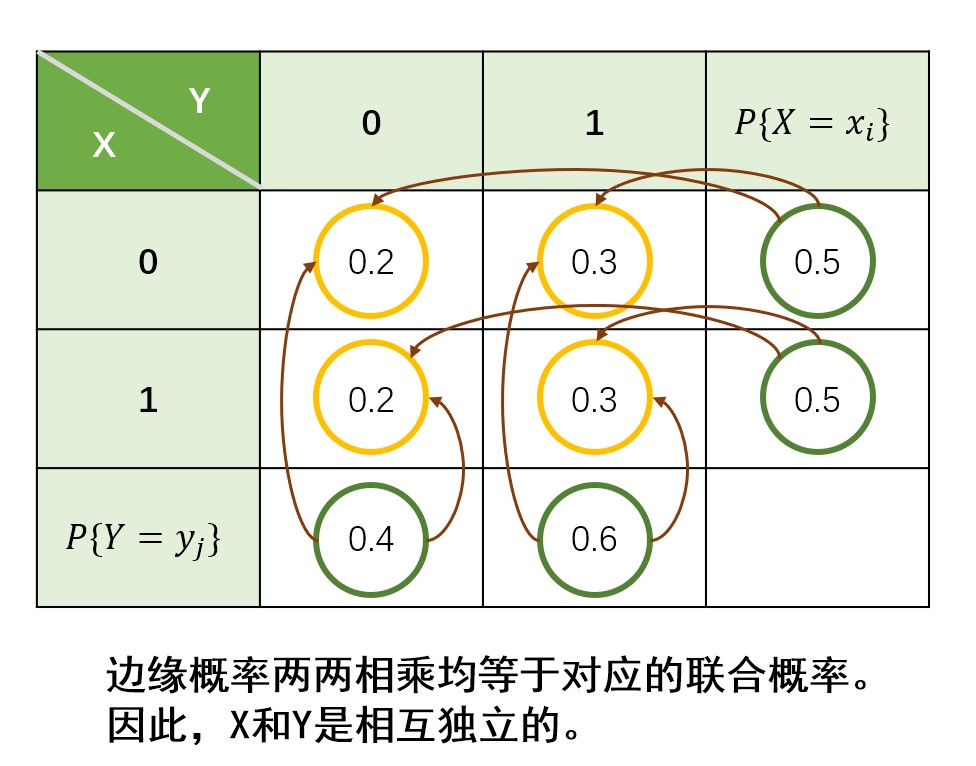
二维连续型的独立性

• \(X,Y\)相互独立的充要条件是\(f(x,y)=f_X(x)f_Y(y)\)。

• 二元正态分布的两个变量相互独立当且仅当\(\rho=0\).

随机变量函数的独立性

如果\(X,Y\)相互独立，则\(g_1(X),g_2(Y)\)相互独立。

使用教材：
《概率论与数理统计》第四版 中国人民大学 龙永红 主编 高等教育出版社