fourier
傅立叶级数是以正余弦函数为基础逼近原周期函数的一种表现形式,它的基础是cos(2 pi w t),则频率的说法来自于正余弦函数.
计算过程:
所以,直流是啥,别问.
复指数形式
---->
你会有疑问为什么n的取值范围是[-N +N],在三角表示的一般形式中,n的范围是[1 N]
把上面的公式带进去,问题会迎刃而解的.
the teacher 说的是正负之内,虚数部分会被抵消,实数部分留存.
因而就有了以下性质:
对于cn的求解到底是怎么回事呢?
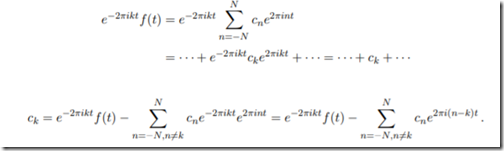
接下来就是奇妙的地方了:
想必你会很疑惑,这是怎么得到的.
原理很简单,ck是一个未知的常数,那么ck在区间[0,1]的定积分就是ck.如此,左右各进行该区间的积分,则得到ck的计算方法.
而在其它不为1的周期内,则会出现1/T的系数,因为后面的正交函数在这个区间内积分才为0啊,笨蛋.
所以,请自觉把周期推到T上去.
部分拓展:
能量:
Let's go to look Fourier transform:
周期的函数有了傅立叶级数,非周期咋整.别急,这不来了吗
我们假设有个周期T不管它是无穷大还是无穷小,它是个数罢了.
然后做傅立叶级数展开:
rect(rectangle) function
then,变魔术了啊
有没有看见第一个里面,因为![]() 的缘故,sin(pi n)/T趋近于0,cn趋近于0,也就是我们爱说的无穷小.
的缘故,sin(pi n)/T趋近于0,cn趋近于0,也就是我们爱说的无穷小.
后面无穷小乘以无穷大,则得到一个有限的值,一个我们可以拿来用的值.
一般形式:
这写起来有点像拉普拉斯变换啊,请自行脑补.
我们不知道是否每一个变换里面无穷大是否一般大小,如果是,那么级数与变换之间的关系应该也唯一确定了吧.
给你加个buff:
那这个玩意怎么表示原函数呢
则:
请自行理解.
就是上面那个玩意儿.
energy spectrum:
feature:





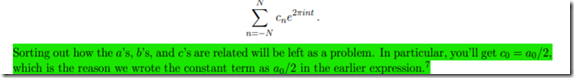
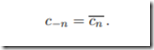


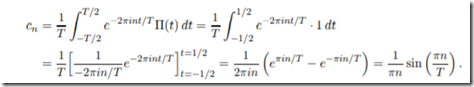
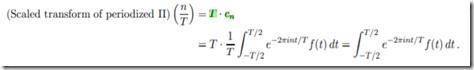
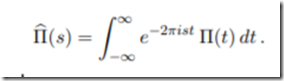

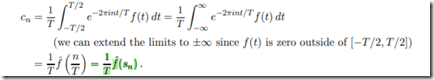

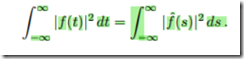

 浙公网安备 33010602011771号
浙公网安备 33010602011771号