树、二叉树和查找总结
思维导图
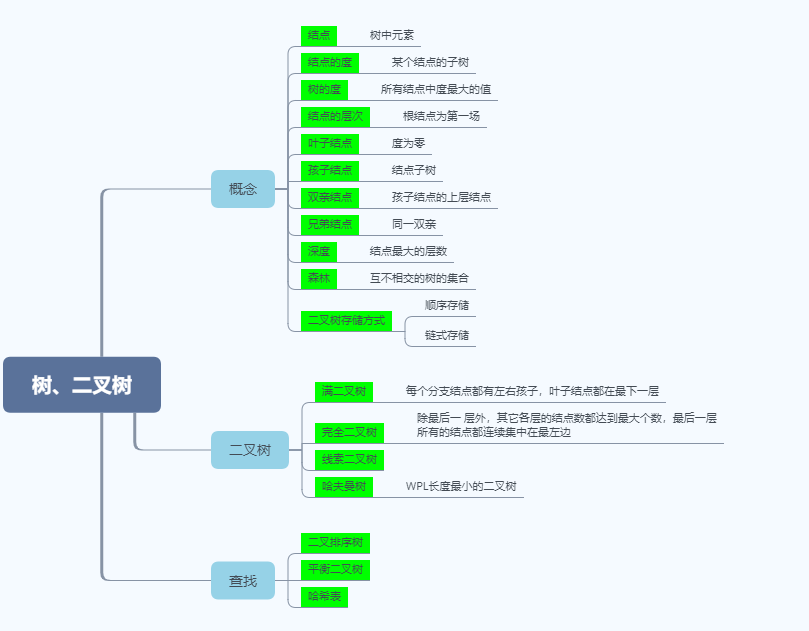
重要的概念
二叉树
-
在二叉树的第K层上,最多有 2k-1 (K >= 1)个结点
-
深度为K的二叉树,最多有 2k - 1 个结点(K>=1)
-
对于任何一棵二叉树,如果其叶子结点的个数为K,度为2的结点数为M,则K=M+1
-
对于一棵有 n 个结点的完全二叉树的结点按层次进行编号,对任意结点 i (1<i<n),有:
如果i=1,则结点i无父结点,是二叉树的根,如果i>1,则父结点为 i/2 向下取整
如果2i>n,则结点i为叶子结点,无左子结点,否则,其左子结点为2i
如果2i+1>n,则结点i无右子结点,否则,其右子结点是结点2i+1
满二叉树
- 如果一颗树深度为h,最大层数为k,且深度与最大层数相同,即k=h;
- 它的叶子数是: 2(h-1)
- 第k层的结点数是: 2(k-1)
- 总结点数是: 2k - 1
- 树高:h=log2(n+1)
- 满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树
二叉排序树
- 若左子树不空,则左子树上所有结点的值均小于它的根节点的值;
- 若右子树不空,则右子树上所有结点的值均大于它的根结点的值
- 没有键值相等的节点
查找
二分查找
-
元素必须有序
-
最坏情况下,关键词比较次数为log2(n+1),时间复杂度为O(log2n)
分块查找
- 选取各块中的最大关键字构成一个索引表
- 先找到在哪一块里再进行顺序查找
哈希表
- 以数据中每个元素的关键字K为自变量,通过散列函数H(k)计算出函数值,以该函数值作为一块连续存储空间的的单元地址,将该元素存储到函数值对应的单元中
- 哈希表查找的时间复杂度为O(1)
- 最常用的方法:除留余数法
哈希冲突的处理方法
线性探测
线性探测法的地址增量di = 1, 2, … , m-1,其中,i为探测次数。该方法一次探测下一个地址,知道有空的地址后插入,若整个空间都找不到空余的地址,则产生溢出
二次探测
类似线性探测,地址增量序列为 di = 1平方, -1平方, 2平方, -2平方,… , q平方, -q平方 (q <= m/2)
链地址法(拉链法)
- 拉链法处理冲突简单,且无堆积现象,平均查找长度较短
- 由于拉链法中各链表上的结点空间是动态申请的,故它更适合于造表前无法确定表长的情况
- 开放定址法为减少冲突,要求装填因子α较小,故当结点规模较大时会浪费很多空间。而拉链法中可取α≥1,且结点较大时,拉链法中增加的指针域可忽略不计,节省空间
- 在用拉链法构造的散列表中,删除结点的操作易于实现
疑难问题
对于数据的处理和构造树表不清楚



 浙公网安备 33010602011771号
浙公网安备 33010602011771号