[PaperReading] DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models

目录

• DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models
• TL;DR
• Method
  • Data Collection
  • DeepSeekMath-Base 7B训练与评估​
  • Reinforcement Learning
  • OneStage Vs TwoStage Training
• Implementation
• Experiment
• 总结与思考
• 相关链接

DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models

link
时间：24.02
单位：DeepSeek
被引次数：1176

TL;DR

提出DeepSeekMath大模型， 在the competition-level MATH benchmark达到51.7%的分数，接近当时的GPT4与Gemini-Ultra。主要改进在于：基于公开数据的data selection pipeline；提出GRPO强化学习算法提升数据推理能力，同时优化了PPO的显存占用。

Method

Data Collection

Pipeline
​​1. 种子数据选择​​
使用高质量数学网页数据集​​OpenWebMath​​作为初始种子，训练​​fastText分类器​​（维度256，学习率0.1），区分数学与非数学内容。
正样本：50万条OpenWebMath数据；负样本：50万条Common Crawl随机网页。
​​2. 迭代数据挖掘​​
​​第一轮​​：从去重后的40B Common Crawl网页中筛选出​​40B数学相关token​​（按分类器得分排名保留高质量部分）。
​​后续迭代​​：通过分析域名（如mathoverflow.net）手动标注数学内容URL，扩充种子数据并更新分类器。经过四轮迭代，最终获得​​35.5M网页（120B token）​​。
​​3. 去污染处理​​
过滤与评测集（如GSM8K、MATH）重叠的内容，避免测试集数据泄露给训练集。

DeepSeekMath-Base 7B训练与评估​

数据配比
56% DeepSeekMath Corpus
4% AlgebraicStack（数学代码）
10% arXiv论文
20% GitHub代码
10% 多语言通用文本

Reinforcement Learning

公式上对比PPO与GRPO
PPO

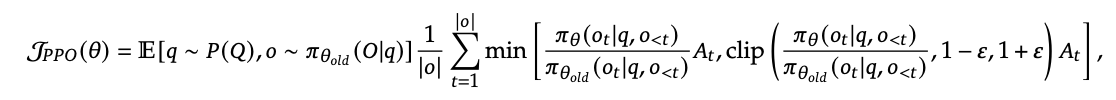
实际实现过程：PPO有四个模型，分别是policy(actor)模型(可训练)、参考模型(SFT后freeze)、奖励模型、价值模型(可训练)

GRPO

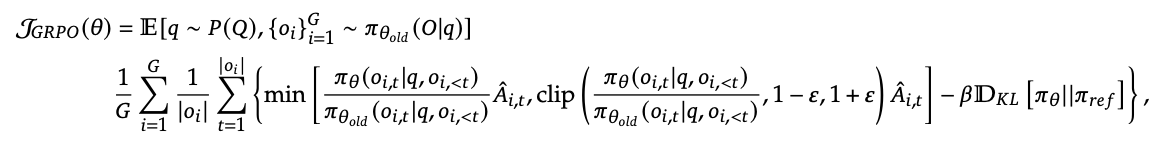
o: action
q: status
\(\pi\): policy
\(r_i\): 第i次response对应的reward
t：第t个token

可以看出，对于同一个output o_{i}的每个token步骤t生成时，其优势函数都一样，仅与output结果有关，而与过程无关。这也是文中4.1.2与4.1.3所论述的基于Outcome Supervision与Process Supervision两种版本，常用GRPO通常指得是前者。

Pipeline对比PPO与GRPO

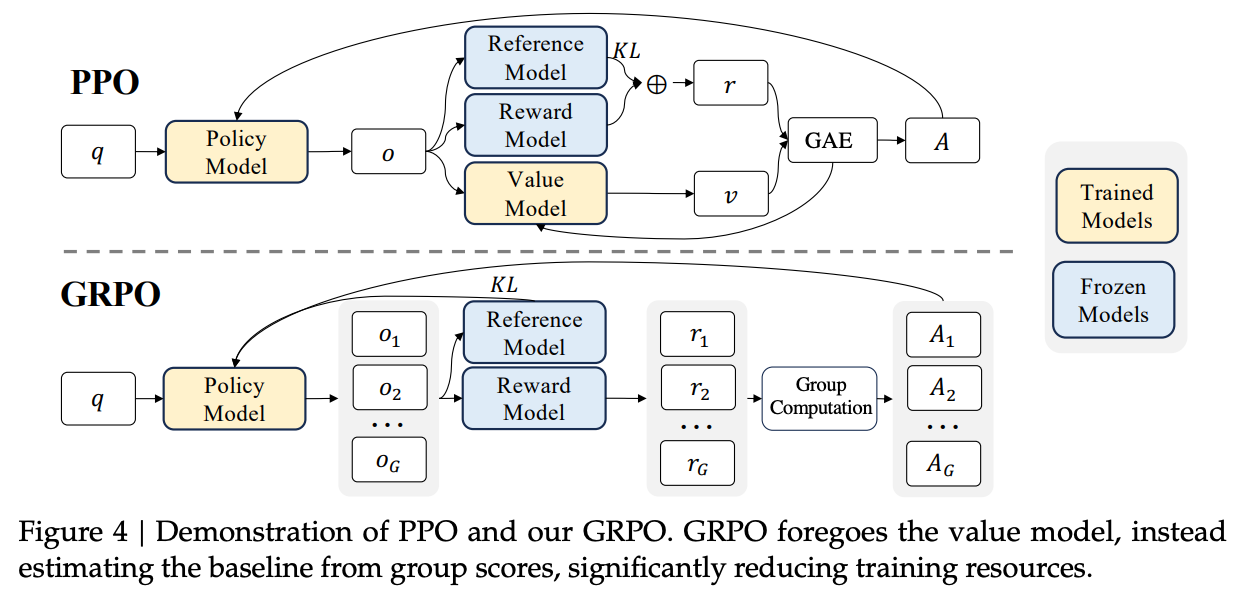
GRPO伪代码

GRPO与PPO区别：
1.GRPO不需要价值模型，使用group内\((r_i - r_{mean})/std(R)\)来代替价值模型预测；
2. 奖励模型每隔一段时间会使用经验回放数据更新一次，而PPO中奖励模型始终Freeze住

OneStage Vs TwoStage Training

​​(1) Two-stage Training（两阶段训练）​​
阶段1（基础训练）​​：
先对模型进行​​纯代码训练​​（400B代码token）或​​通用文本训练​​（对照组）。
代码训练数据：GitHub代码（数学相关代码库如AlgebraicStack占比4%）。
通用文本训练：Common Crawl中的自然语言数据。
阶段2（数学专项训练）​​：
在阶段1基础上，继续用​​数学语料​​（150B token，含DeepSeekMath Corpus、arXiv等）训练。
目标：使模型融合代码的逻辑能力与数学知识。
​​(2) One-stage Training（单阶段训练）​​
直接混合​​代码数据（400B token）​​与​​数学数据（150B token）​​，一次性训练完成。
数据比例：代码:数学 ≈ 2.7:1（与两阶段的总量相同，但无明确阶段划分）。

Implementation

​​超参数​​：学习率4.2e-4，批量大小10M token，训练500B token。

Experiment

清洗数据的收益

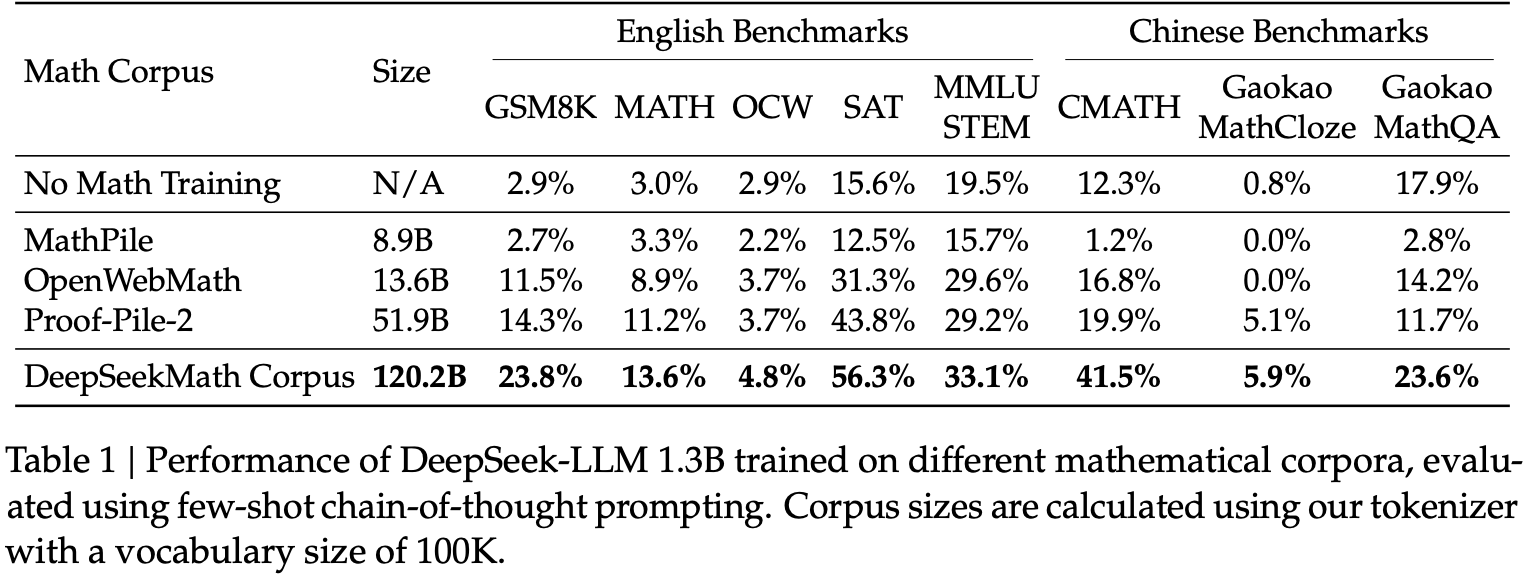
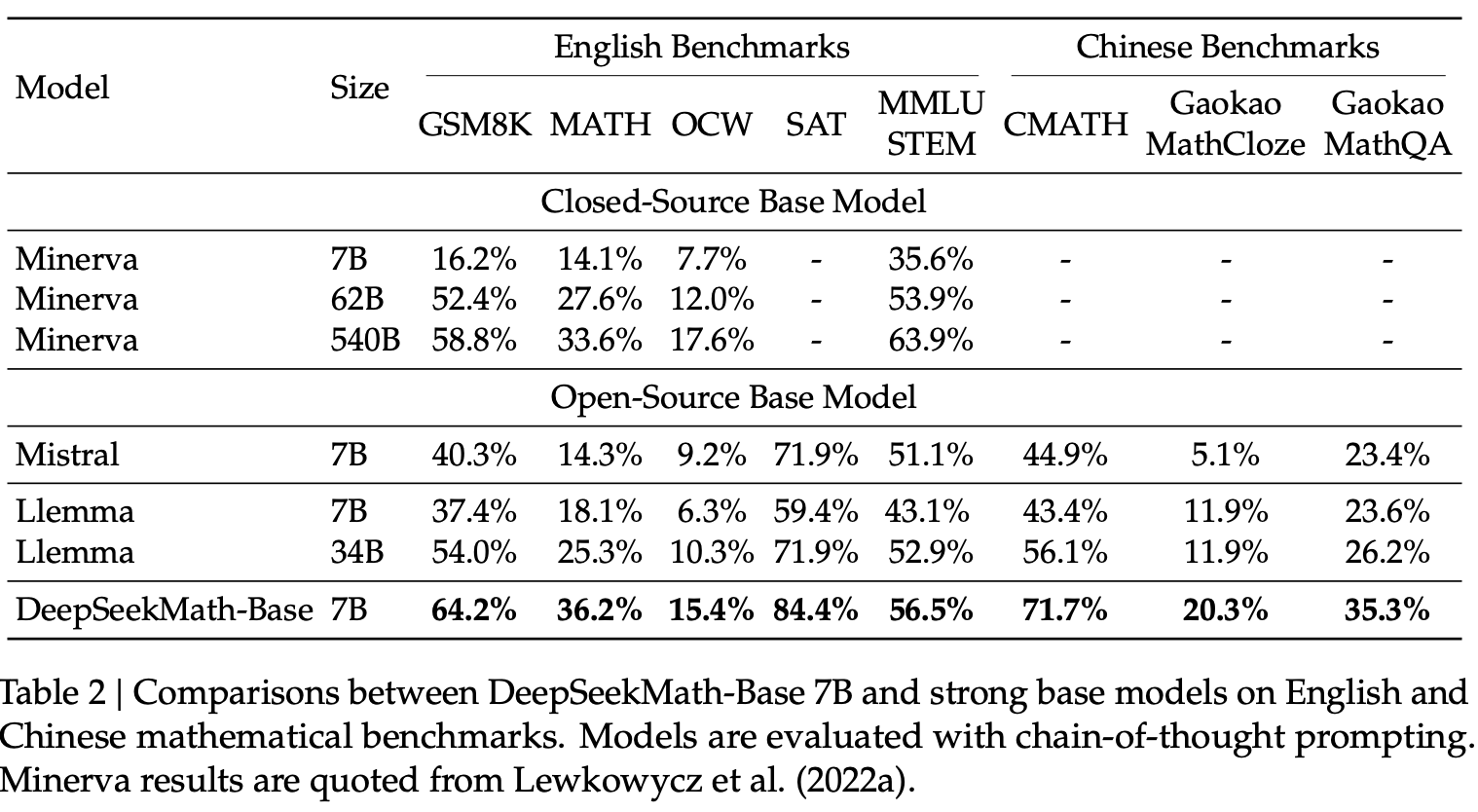
竞品对比

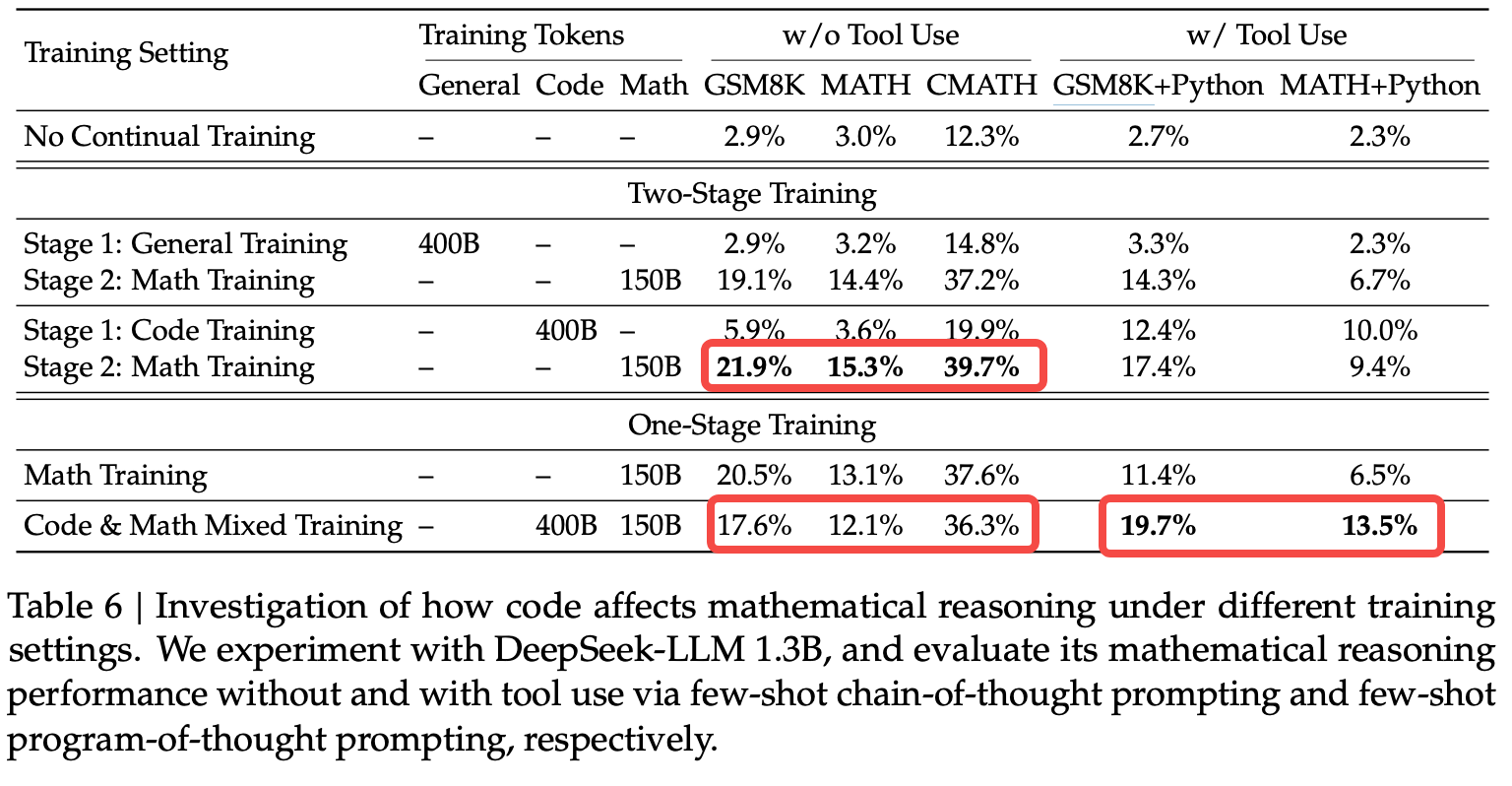
OneStage Vs TwoStage
OneStage Coding能力好，相对于TwoStage数学差一些，但多任务效果更均衡

总结与思考

无

相关链接

https://zhuanlan.zhihu.com/p/708304022