9近似算法
近似算法
1 概述
- 迄今为止,所有的NP完全问题,均未能找到多项式时间的算法,故当问题规模较大时,求得最优的精确解的可能性很小
- 迄今为止,所有的NP完全问题,均未能找到多项式时间的算法,故当问题规模较大时,求得最优的精确解的可能性很小
2 近似算法的性能
- 近似算法一般都比较简单,但设计近似算法时必须关注所设计的算法所得到的近似解与最优解之间的差距到底有多大
- 若一个最优化问题的最优值为 c* ,求解该问题的一个近似算法求得的近似最优解相应的目标函数值为c,则将该近似算法的近似比定义为max{c*/c, c/ c *},近似比永远大于等于1
- 在通常情况下,近似比是问题输入规模n的一个函数ρ(n),即max{c */c, c/ c *}≤ρ(n)
3 近似方案
- 常数近似比的近似算法
- 多项式时间近似方案(PTAS, Polynomial Time Approximation Scheme)
- 完全多项式时间近似方案(FPTAS, Fully Polynomial Time Approximation Scheme)
4 装箱问题
问题
- 设有n个物体u1,u2,…,un,每个物体的体积不超过1。另外,有足够多的、体积为1的箱子。箱子、物体均是长方体且截面相同(所有物体都能放入到箱子中)
- 问如何装箱,使得所用箱子数最少?
First-Fit(FF)算法
- 从排在最前面的箱子开始,对每个箱子剩余的体积逐一进行检查,一旦碰到第一个能够装进当前物体的箱子时,就立即把该物体装入这个箱子。对每个物体反复执行上述程序
- 算法的最坏时间复杂度:O(n2)
- 用FF算法不能保证所获得的解是最优解
- 分析
- 记号I:表示某一问题的任一实例
- OPT(I):表示该实例的最优解
- FF算法满足:对于任何装箱实例I,都有FF(I)≤2OPT(I)
- 更为准确地,对所有装箱问题的实例I,都有FF(I)≤17/10 OPT(I),且存在OPT(I)任意大的实例I,使得FF(I)≥17/10(OPT(I)-1)
Next-Fit(NF)算法
- 先把第一个空箱置为当前箱。然后依次把物品u1,u2,…,un按下列方式装箱:若当前所指的箱子里放得下ui,则把ui放入箱中;若放不下则把ui放入下一个空箱,把当前指针指向(放ui的)该箱
- 算法的最坏时间复杂度:O(n)(因为对每个物品只检查当前的箱子)
- 分析
- NF算法满足:对于任何装箱实例I,都有NF(I)≤2OPT(I)-1
Best-Fit(BF)算法
- FF算法的修改:在已装有物品的箱子中,找一个既能放下ui、又使得其剩余空间最小的箱子来放ui
- 表面上看起来该算法要比FF法更能充分利用空间,但实际上,Johnson等人证明了BF法在最坏情况下的性能,本质上与FF法相同
FFD(First-Fit Decreasing)算法
- 先将所有物品从大到小排序,然后再使用FF法
- 对一切装箱实例I,有FFD(I)≤4/3 OPT(I),当OPT(I)=3k+1时,有FFD(I)≤⌊4/3 OPT(I) ⌋
- 对所有装箱问题的实例I,有FFD(I)≤11/9OPT(I)+1 (1990)
5 顶点覆盖问题
问题
- 无向图G=(V,E)的顶点覆盖是它的顶点集V的一个子集V’⊆V,使得若(u,v)是G的一条边,则v∈V’或u∈V’,顶点覆盖V’的大小是它所包含的顶点个数|V’|
- 简单来说就是使得图中的每一条边)都至少接触集合中的一个顶点。寻找最小的顶点覆盖的问题称为顶点覆盖问题,它是一个NP完全问题
近似算法
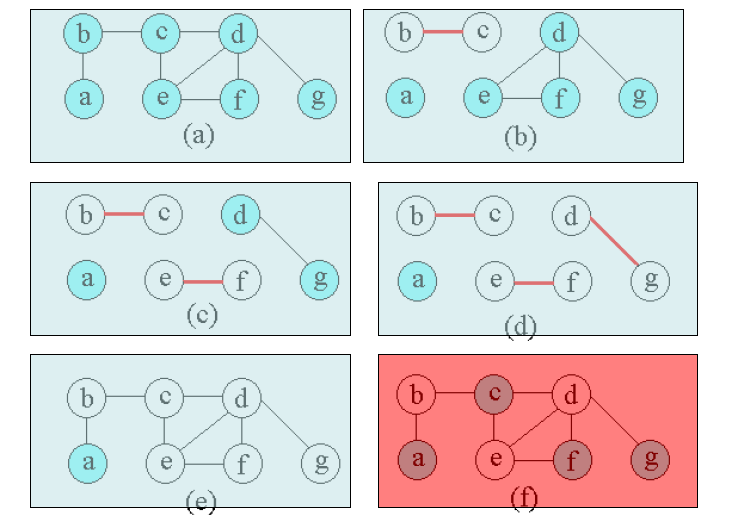
- 下面的近似算法以无向图G为输入,并计算出G的近似最优顶点覆盖,可以保证计算出的近似最优顶点覆盖大小不会超过最小顶点覆盖大小的2倍
//伪代码
VertexSet approxVertexCover ( Graph g )
{ cset=空集;
e1=g.e;
while (e1 != 空集) {
从e1中任取一条边(u,v);
cset=cset∪{u,v};
从e1中删去与u和v相关联的所有边;
}
return c
}
- Cset用来存储顶点覆盖中的各顶点。初始为空,不断从边集e1中选取一边(u,v),将边的端点加入cset中,并将e1中已被u和v覆盖的边删去,直至cset已覆盖所有边。即e1为空。
- 图(a)~(e)说明了算法的运行过程及结果。(e)表示算法产生的近似最优顶点覆盖cset,它由顶点b,c,d,e,f,g所组成。(f)是图G的一个最小顶点覆盖,它只含有3个顶点:b,d和e
6 旅行商问题
问题
- 一个旅行商人必须访问n个城市,这个旅行商人想要进行一次巡回旅行,或经过哈密顿回路,恰好访问每个城市一次,并最终回到出发城市。旅行所需的全部费用是他旅行中从一个城市到另一个城市的费用的总和,作为商人,他希望整个旅行的费用最低,求此次旅行的路径规划。
- 简单来说:在一个具有n个顶点的无向赋权完全图中,找到一条权值总和最小的哈密顿回路。
- 注意:这里我们所说的TSP问题特指对称TSP问题,两座城市之间来回的距离是相等的,形成的是一个无向图。而在非对称TSP问题中,可能不是双向的路径都存在,或是来回的距离不同,形成的是有向图
满足三角不等式的TSP问题
- 什么是满足三角不等式:在很多实际情况中,从一个地方u到另一个地方w花费的代价总是最小的。如果一条路径经过了某个中转站,则它不可能具有比直接到达更小的代价。将这种情况形式化,即如果对所有的顶点 u , v , w ∈ V 有:c ( u , w ) ⩽ c ( u , v ) + c ( v , w )就称代价函数c cc满足三角不等式
- 不过即使代价函数满足三角不等式,也不能改变旅行商问题的NP完全性。因此不能寄希望于找到一个准确解决旅行商问题的多项式时间算法,但是相反,我们可以寻找到一些好的近似算法
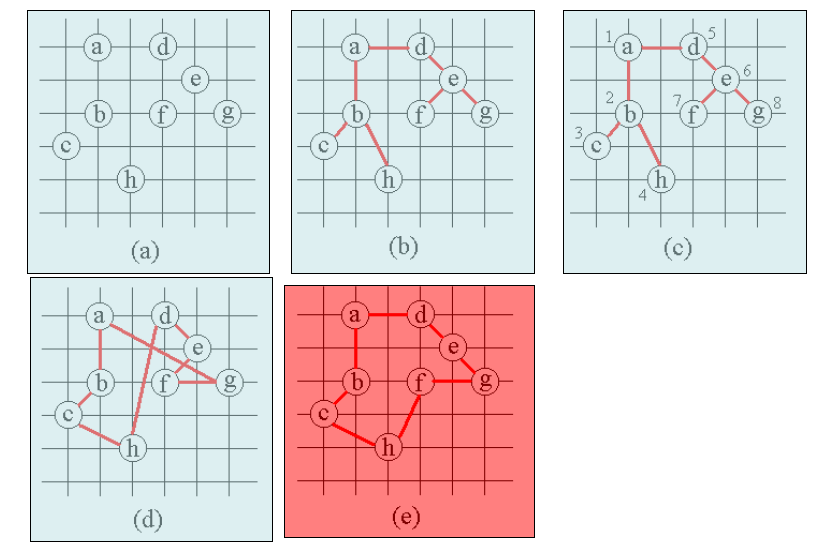
近似算法--最小生成树法
- 对于给定的无向图G,可以利用找图G的最小生成树的算法设计找近似最优的旅行售货员回路的算法
- 当代价函数满足三角不等式时,算法找出的路径的代价不会超过最优路径的代价的2倍

一般的旅行商问题
- 在代价函数不一定满足三角不等式的一般情况下,不存在具有常数近似比的解TSP问题的多项式时间近似算法,除非P=NP
- 换句话说,若P≠NP,则对任意常数ρ>1,不存在近似比为ρ的求解旅行商问题的多项式时间近似算法




 浙公网安备 33010602011771号
浙公网安备 33010602011771号