8NP完全性

NP完全性

1 两大类问题（非严格分类）

​ 多项式时间

• 排序 O(nlogn)
• Ordered searching O(logn)
• 最大元，最小元 O(n)

​ 非多项式时间

• 旅行商问题 O(n^2 * 2^n )
• 背包问题 O(2 ^ n/2)

2 计算的模型

​ 自动机理论

• 有限自动机(FA)
  • 存储量极小的计算机
  • 在文本处理,编译程序及硬件设计中有应用
• 下推自动机(PDA)
  • 带一个栈的计算机
  • 在程序设计语言和人工智能中有应用
• 图灵机(TM)
  • 有无限可改写存储的计算机
  • 能解决实际计算机所能解决的一切问题
• FA和PDA是简化的图灵机
• 一般将以图灵机作为计算的理论模型

​ 计算模型

• 分类
  • RAM
  • RASP
  • 确定性Turing机
  • 非确定性Turing机
• 计算模型是计算机科学的重要组成部分
• NP-完全概念的原始定义需要借助非确定性Turing机等计算模型的概念

​ Random Access Machines（RAM）

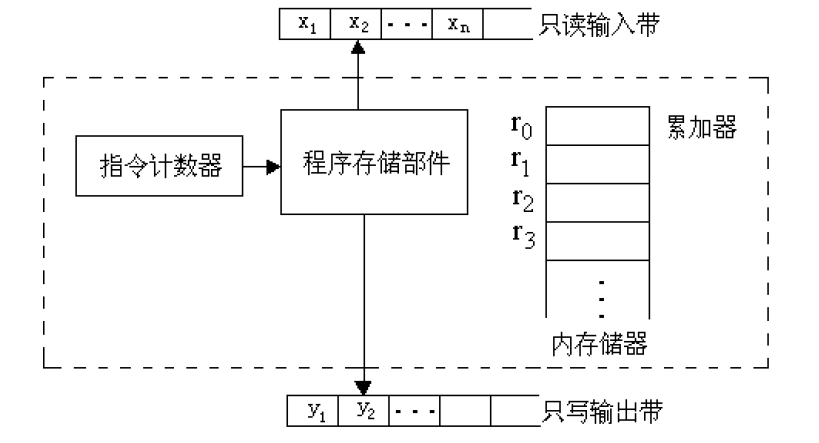
• 一个RAM程序定义了从输入带到输出带的一个映射。可以对这种映射关系作2种不同的解释
• 把RAM程序看成是计算一个函数
• 把RAM程序当作一个语言接受器

​ Random Access Stored Program（RASP）

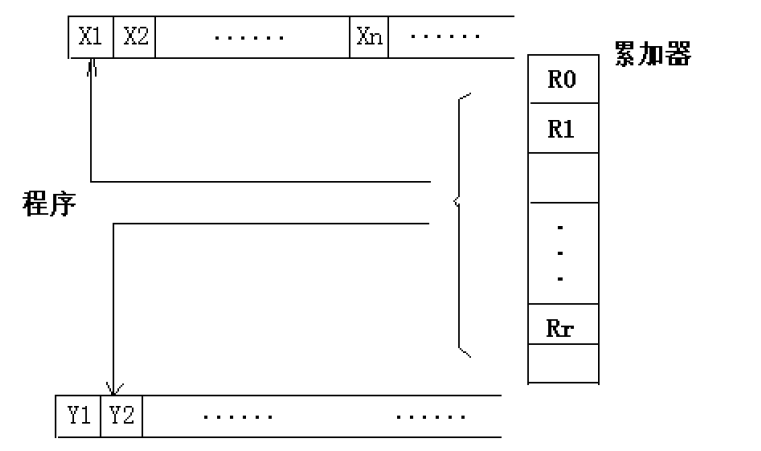
• RASP的整体结构类似于RAM，所不同的是RASP的程序是存储在寄存器中的。每条RASP指令占据2个连续的寄存器。第一个寄存器存放操作码的编码，第二个寄存器存放地址

3 Turing机

​ 历史

• 什么是计算？什么问题是可计算的？
• Turing 认为计算是一个人拿一支笔在一张纸上进行的操作，输入是眼睛看到的符号，根据脑中的规则在纸上擦掉或写上一些符号；再用眼睛看下面的符号，根据规则进行擦写的工作；重复上述工作，直到这个人认为可以结束为止。此时，最后写下的符号就是所要的结果。
• 特点：在这个（计算）过程中，只用到了有穷多个符号
• Turing 根据这个过程构造出了一个计算模型，称之为Turing机

• Turing发现该模型可以实现非常复杂的计算
• Turing称：凡是Turing机可以计算的问题就是可计算的，否则就是不可计算的（不足）；由此引出可计算性理论的研究
• Church-Turing Thesis（丘奇-图灵论题）：任何合理的计算模型都是相互等价的（计算范围相同）（合理：单位时间内可以完成的工作量，有一个多项式的上限）
• 迄今为止所有被提出的合理计算模型均满足该论题

​ Truing机的形式

• 单带双向Turing机
• 单带单向Turing机
• 多带双向Turing机
• 多带单向Turing机
• 已经证明，这些Turing机的计算能力（在多项式意义下）相同

​ 非确定性Turing机

• 一般地说，将可由多项式时间算法求解的问题看作是易处理的问题，而将需要超多项式时间才能求解的问题看作是难处理的问题
• 有许多问题，从表面上看似乎并不比排序或图的搜索等问题更困难，然而至今人们还没有找到解决这些问题的多项式时间算法，也没有人能够证明这些问题需要超多项式时间下界
• 在图灵机计算模型下，这类问题的计算复杂性至今未知
• 为了研究这类问题的计算复杂性，人们提出了另一个能力更强的计算模型，即非确定性图灵机计算模型，简记为NDTM(Nondeterministic Turing Machine)
• 在非确定性图灵机计算模型下，许多问题可以在多项式时间内求解
• 一台k带DTM（确定性Turing机）根据其当前所在状态及k个读写头当前读到的字符唯一地确定下一步的动作；与DTM不同的是，NDTM的每一步动作允许有若干个选择

4 从图灵机角度得到问题的分类

​ P类问题和NP类问题

• P类问题：一个判定问题中的每一个实例编码为一个符号串ω，使得该实例的回答为Yes当且仅当它的编码ω在多项式时间里被一台DTM所接受，则称该判定问题属于P类
• NP类问题：一个判定问题中的每一个实例编码为一个符号串ω，使得该实例的回答为Yes当且仅当它的编码ω在多项式时间里被一台NDTM所接受，则称该判定问题属于NP类

​ 判定问题和最优化问题

• 判定问题：：回答是“Yes”或“No”
• 最优化问题（不是Yes-No问题）可以与一个判定问题相对应
  • 比如，最优化问题：团集问题(CLIQUE)：任给一个无向图G，找出G中最大的团集。团集：点的集合，满足：任两点之间均有边相连
  • 对应的判定问题：G中是否有k-团（k个顶点的团集）？
• 相关问题举例
  • 图着色问题：给定无向连通图G和m种不同的颜色。用这些颜色为图G的各顶点着色，每个顶点着一种颜色。是否有一种着色法使G中每条边的2个顶点着不同颜色
  • 01背包问题
  • 子集总和问题：给出一个正整数C和n个物体，每个物体的大小为si。是否有一个物体的子集，其大小相加正好等于C？
  • 汉密尔顿(Hamilton)问题：给定一个无向图G，G是否有哈密顿循环或哈密顿路径？
  • 旅行商问题

​ 证书

• 定义：：若集合S包含判定问题A的所有解，则称S是A的证书集，S中的元素称为A的一个证书（certificate，注意证书不一定是解）

• 举例

  • k-团问题
    • 问题描述：在一无向图中找出一个点数最多的完全图（k团就是点数为k的完全图可以找到吗）
    • 给定无向图G=(V,E)，顶点集V的任何一个k顶点子集V’就是k-团问题的一个证书
    • 如果Q 是k-团问题的解，则一定有Q∈S
  • Hamilton路径问题
    • 哈密顿通路（回路）与哈密顿图 （Hamilton图） 通过图G的每个结点一次，且仅一次的通路（回路），就是哈密顿通路（回路）。存在哈密顿回路的图就是哈密顿图
    • 给定无向图G=(V,E)，任何一个由n个互不相同的顶点构成的序列就是H路径问题的一个证书
    • 如果图G有Hamilton路径，则该路径一定属于S

  

  • SAT问题
    • 给定一个布尔方程，判断是否存在一组布尔变量的取值方案，使得整个方程式的值为真，这种问题被称为布尔方程的可满足性问题（SAT）。SAT问题被证明是NP完全的，当k > 2的时候我们无法在多项式时间之内求解，但是对于一些特殊的SAT（比如2-SAT）我们可以有效求解
    • 给定一个n元的布尔表达式f(x1,x2,…,xn)，则n元组(α1, α2,…, αn) (αi或为0或为1，已确定)为该问题的一个证书
    • 若f(x1,x2,…,xn)可满足，则使f(x1,x2,…,xn)为1的n元组含在其中

5 再看P类问题和NP类问题

• 若判定问题A满足：1、有证书集S；2、存在一个算法F，对于S中的每一个证书α，F都能够在多项式时间里验证α是否为A的一个解，则称A∈NP

​ 定义

• P类问题是多项式时间可解的
• NP类问题是多项式时间可验证的

​ 证书问题验证

• k-团问题
  • 对于任给的一个证书V’（k顶点子集即|V’|=k），只要逐一检查V’中的任意两点之间是否有边
  • 这样的点共有k(k-1)/2个，若每个点对间均有边相连，则V’是一个k-团，否则不是
  • 验证算法时间为Θ(k2)，故是多项式时间可验证的
• Hamilton路径问题
  • 对于任给的一个证书即序列，只要逐一检查序列中相邻点之间是否有边相连
  • 若n-1个相邻点对均有边相连，则该序列是Hamilton路径，否则不是
  • 验证算法时间为Θ(n)，故是多项式时间可验证的
• SAT问题
  • 对于任给的一个证书即n元组(α1, α2,…, αn)
    (αi或为0或为1，已确定)，只要把这n个具体的0或1值代入布尔表达式f(x1,x2,…,xn)，进行逻辑运算后即可知f(α1, α2,…, αn)的值为0还是为1
  • 若f(x1,x2,…,xn)的长度为m，则计算f(α1, α2,…, αn)的时间为Θ(m)，故是多项式时间可验证的

6 NPC问题

• 非形式定义，如果一个问题属于NP类，且与NP类中的任何问题是一样“难”的，则说它属于NP-C类，也称其是NP完全的（NP-Complete）

​ 定义

• NPC类问题是迄今为止未发现有多项式求解方案的
• 验证Npc问题的两个方法：多项式变换(规约)和限制法

​ 多项式变换（规约）

• 设IA是判定问题A的任一实例，B是另一判定问题，若存在一个从A到B的映射f满足
  • ∀IA∈A ，实例IA的答案为‘Yes’ iff(当且仅当) f(IA)（与IA相对应的B问题的实例）的答案为‘Yes’
  • ∀IA∈A，若IA的输入规模为n，则对应实例f(IA)的输入规模不超过PA(n)，这里PA(n)是一个与判定问题A有关的多项式
  • ∀IA∈A ，若IA的输入规模为n，则对应实例f(IA)的输入在多项式时间p(n)内可计算
• 则称问题A可多项式变换为B，记作A≤pB，(≤p亦称Karp规约)
• 若A≤pB且问题B是多项式时间可判定的，则问题A也一定是多项式时间可判定的
• 要证明一个判定问题B是NP-C的，除了要证明B是多项式时间可验证的（从而B属于NP类），还要找一个NP-C问题A，证明A可以在多项式时间里变换为B，且A的任一实例回答为‘Yes’ iff与之对应的B的实例回答为‘Yes’

​ NPC问题举例

• k-团问题
  • 证明思路：3 SAT是NP完全问题，证明3 SAT≤p CLIQUE（k-团问题)
• 顶点覆盖问题
  • 问题：顶点覆盖的最优化问题：在一个无向图G中，找一个顶点数最少的顶点集，满足：任一条边的两个顶点中至少有一个在此集合中；顶点覆盖的判定问题：无向图G中是否存在顶点数为k的顶点覆盖？
  • 证明思路：先证明其属于NP，再证明CNF-SAT≤pVC
• 子集和问题
  • 有一个数集A={a1,a2,…,an}及一个目标数S，问A中是否能找出一个子集A’，使得A’中元素之和为S？
  • 证明思路：首先证明其是NP问题，再证明3CNF-SAT≤pSubset-Sum
• 击中集问题
  • 设F是一个由S的某些子集构成的集合族。给定正整数k，问是否存在S的子集S’满足S’属于S，|S’|≤k，使得S’包含F中每一个子集里的至少一个元素？（满足条件的子集S’称为F的击中集。）
• 01背包问题

​ 限制法

• 要证明问题π∈NP-C，先证明π∈NP，再找一个已知的NP-C问题π’，证明π’是π的特例（在π上加了一些限制），从而立即有π’≤pπ

7 NP-hard问题

​ 定义

• NP-hard类问题是迄今为止未发现有多项式求解方案的，且 NP-hard问题不一定是判定问题

​ 求解方法

• 当n不太大时，可使用a)动态规划法b)分枝限界法c)回溯法
• 求近似解。在误差允许的范围之内找一个解，该近似解可以在多项式时间里得到
• 用启发式算法求解，根据具体问题设计启发式搜索策略，在理论上往往缺乏严格的证明，用实验数据说明算法很有效
• 智能优化算法，常常能获得很好的结果。但有偶然性，与最优解的误差难以给出

8 总结

• P,NP,NPC一定是判定问题，但NP-hard不一定是判定问题
• P类问题是多项式时间可解的
• NP类问题是多项式时间可验证的
• NPC类问题是迄今为止未发现有多项式求解方案的
• NP-hard类问题是迄今为止未发现有多项式求解方案的，且 NP-hard问题不一定是判定问题