7回溯算法
回溯法
1 回溯法概述
简单思想
- 回溯法思路的简单描述是:把问题的解空间转化成了图或者树的结构表示,然后使用深度优先搜索策略进行遍历,遍历的过程中记录和寻找所有可行解或者最优解
详细描述
- 回溯法按深度优先策略搜索问题的解空间树。首先从根节点出发搜索解空间树,当算法搜索至解空间树的某一节点时,先利用剪枝函数判断该节点是否可行(即能得到问题的解)。如果不可行,则跳过对该节点为根的子树的搜索,逐层向其祖先节点回溯;否则,进入该子树,继续按深度优先策略搜索
- 回溯法的基本行为是搜索,搜索过程使用剪枝函数来为了避免无效的搜索。剪枝函数包括两类:1. 使用约束函数,剪去不满足约束条件的路径;2.使用限界函数,剪去不能得到最优解的路径
- 问题的关键在于如何定义问题的解空间,转化成树(即解空间树)。解空间树分为两种:子集树和排列树。两种在算法结构和思路上大体相同
应用
- 当问题是要求满足某种性质(约束条件)的所有解或最优解时,往往使用回溯法
- 它有“通用解题法”之美誉
分析
- X=(x1,x2...xn),xi取值为有限集Si,解空间为S1*S2 ... * Sn,所以第2层有S1个节点,第3层有S1 S2个节点...
- 可能会遇到解空间无限的情况,比如图里面存在环
- 用回溯法解题的一个显著特征是在搜索过程中动态产生问题的解空间。在任何时刻,算法只保存从根结点到当前扩展结点的路径。
- 如果解空间树中从根结点到叶结点的最长路径的长度为h(n),则回溯法所需的计算空间通常为O(h(n)),而显示地存储整个解空间则需要O(2 ^ h(n)) 或O(h(n)!)内存空间、
2 递归回溯和迭代回溯
递归回溯
- 回溯法对解空间作深度优先搜索,因此,在一般情况下用递归方式实现回溯法
//针对N叉树的递归回溯方法
void backtrack (int t)
{
if (t>n) output(x); //叶子节点,输出结果,x是可行解
else
for i = 1 to k//当前节点的所有子节点
{
x[t]=value(i); //每个子节点的值赋值给x
//满足约束条件和限界条件
if (constraint(t)&&bound(t))
backtrack(t+1); //递归下一层
}
}
迭代回溯
- 采用树的非递归深度优先遍历算法,可将回溯法表示为一个非递归迭代过程
//针对N叉树的迭代回溯方法
void iterativeBacktrack ()
{
int t=1;
while (t>0) {
if(ExistSubNode(t)) //当前节点的存在子节点
{
for i = 1 to k //遍历当前节点的所有子节点
{
x[t]=value(i);//每个子节点的值赋值给x
if (constraint(t)&&bound(t))//满足约束条件和限界条件
{
//solution表示在节点t处得到了一个解
if (solution(t)) output(x);//得到问题的一个可行解,输出
else t++;//没有得到解,继续向下搜索
}
}
}
else //不存在子节点,返回上一层
{
t--;
}
}
}
3 子集树和排列树
简介
- 回溯法求解时常见的两类解空间树
- 子集树:当所给问题是从n个元素的集合S中找出S满足某种性质的子集时,相应的解空间树称为子集树
- 排列树:当所给问题是确定n个元素满足某种性质的排列时,相应的解空间树称为排列数
子集树
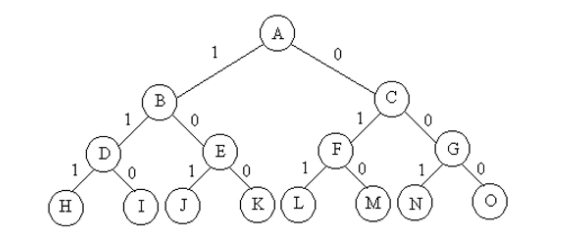
- 子集树,通常S1=...Sn=C,各节点有相同数目子树,C=2时,子集树中共有2n个叶子,因此需要O(2n)时间
排列数
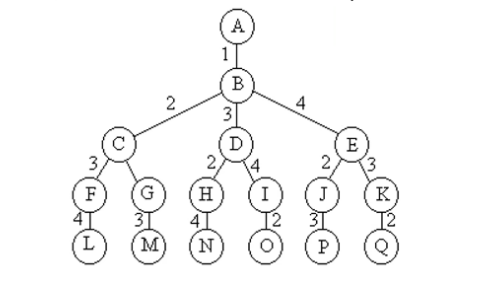
- 排列数,通常S1=n,...,Sn=1,所以排列树中共有n!个叶子节点,需时间O(n!)
4 0-1背包问题
问题
- 给定n种物品和一背包。物品i的重量是wi,其价值为vi,背包的容量为C。问应如何选择装入背包的物品,使得装入背包中物品的总价值最大?
- 0-1背包问题是一个特殊的整数规划问题
思想
-
解空间:子集树
-
约束:w1+w2+...wi+...<=C
-
整体思想: 01背包属于找最优解问题,用回溯法需要构造解的子集树。对于每一个物品i,对于该物品只有选与不选2个决策,总共有n个物品,可以顺序依次考虑每个物品,这样就形成了一棵解空间树: 基本思想就是遍历这棵树,以枚举所有情况,最后进行判断,如果重量不超过背包容量,且价值最大的话,该方案就是最后的答案。
public class bag01 {
public int[] weight;//存重量
public int[] value;//存价值
public int[] take;//存拿还是不拿
int curWeight = 0;
int curValue = 0;
int bestValue = 0;
int[] bestChoice;
int count;
int maxWeight = 0;
public void init(int[] weight, int[] value, int maxWeight) {
if (weight == null || weight.length == 0
|| value == null || value.length == 0
|| weight.length != value.length || maxWeight <= 0) {
System.out.println("args wrong!");
return;
}
this.value = value;
this.weight = weight;
this.maxWeight = maxWeight;
count = value.length;
take = new int[count];
bestChoice = new int[count];
}
public int[] maxValue(int x) {
//走到了叶子节点
if (x > count - 1) {
//更新最优解
if (curValue > bestValue) {
bestValue = curValue;
for (int i = 0; i < take.length; i++) {
bestChoice[i] = take[i];
}
}
} else {
//遍历当前节点(物品)的子节点:0 不放入背包 1:放入背包
for (int i = 0; i < 2; i++) {
take[x] = i;
if (i == 0) {
//不放入背包,接着往下走
maxValue(x + 1);
} else {
//约束条件,如果小于背包容量
if (curWeight + weight[x] <= maxWeight) {
//更新当前重量和价值
curWeight += weight[x];
curValue += value[x];
//继续向下深入
maxValue(x + 1);
//回溯法重要步骤,个人感觉也是精华所在。
// 当从上一行代码maxValue出来后,需要回溯容量和值
curWeight -= weight[x];
curValue -= value[x];
}
}
}
}
return bestChoice;
}
public static void main(String[] args) {
bag01 bt=new bag01();
bt.init(new int[]{16,15,15},new int[]{45,25,25},30);
int[] result = bt.maxValue(0);
System.out.print("最佳选择为:[");
for(int i=0;i<bt.bestChoice.length;i++) {
if(i==bt.bestChoice.length-1) {
System.out.print(bt.bestChoice[i]+"]");
}else {
System.out.print(bt.bestChoice[i]+",");
}
}
System.out.print("\n此时价值最大,即"+bt.bestValue);
}
}
5 装载问题
问题
- 有一批共n个集装箱要装上2艘载重量分别为c1和c2的轮船,其中集装箱i的重量为wi,且所有集装箱总和<=(c1+c2)
- 装载问题要求确定是否有一个合理的装载方案可将这个集装箱装上这2艘轮船。如果有,找出一种装载方案
思想
- 容易证明,如果一个给定的装载问题有解,则采用如下的策略可以得到最优装载方案: 1首先将第一艘轮船尽可能装满;2将剩余的集装箱装上第二艘轮船
- 将第一艘轮船尽可能的装满等价于选取全体集装箱的子集,使该子集中集装箱的重量之和最接近 c1 。因此,等价于一个特殊的0-1背包问题。 因此是一棵子集树
- 用回溯法设计解装载问题的O(2 ^n)计算时间算法。在某些情况下该算法优于动态规划算法
public class zhuangzai2 {
private int n;//集装箱数
private int[] w;//集装箱重量数组
private int c;//第一艘轮船的载重量
private int cw;//当前载重量
private int bestw;//当前最优载重量
private int r;//剩余集装箱重量
private int[] x;//当前解
private int[] bestx;//当前最优解
/**
这步是核心!!
*/
public void backtrace(int i) {
//1.到达叶节点
if (i > n-1) { //i此时的值=叶节点+1
if (cw > bestw) {
for (int j = 0; j < n; j++) {
bestx[j] = x[j];
bestw = cw;
}
return;
}
}
r -= w[i];
//2.搜索左子树 表示将集装箱装入第一个箱子
//以下这个就是约束函数
if (cw + w[i] <= c) {
x[i] = 1;
cw += w[i];
backtrace(i + 1);
cw -= w[i];
}
//3.搜索右子树 表示不把集装箱装入第一个箱子
//下面这个判断条件就是剪枝函数(限界函数),如果不大于当前最优重量就压根不需要去求了
if (cw + r > bestw) {
x[i] = 0;
backtrace(i + 1);
}
r += w[i];
}
public static void main(String[] args) {
zhuangzai2 X = new zhuangzai2();
//货物数量
Scanner scanner = new Scanner(System.in);
String s1 = scanner.nextLine();
X.n = Integer.parseInt(s1);
X.w = new int[X.n];
X.x = new int[X.n];
X.bestx= new int[X.n];
System.out.println("输出货物的重量数组:");
for (int i = 0; i < X.n; i++) {
X.w[i] = (int) (100 * Math.random());
System.out.println(X.w[i]);
}
//第一艘船的载重量
String s2 = scanner.nextLine();
X.c = Integer.parseInt(s2);
for (int i = 0; i < X.n; i++)
X.r += X.w[i];
X.backtrace(0);
System.out.print("输出当前最优解:");
for (int i = 0; i < X.n; i++) System.out.print(X.bestx[i] + " ");
System.out.println();
System.out.println("最优解:" + X.bestw);
}
}
6 符号三角形问题
问题
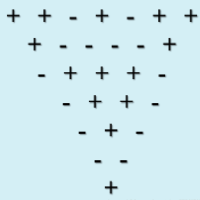
- 下图是由14个“+”和14个“-”组成的符号三角形。2个同号下面都是“+”,2个异号下面都是“-”
- 符号三角形第一行有n个符号,符号三角形问题要求对于给定的n,计算有多少个不同的符号三角形,使其所含的“+”和“-”的个数相同
思路
- 不断改变第一行的每个符号,搜索符合条件的解,可以使用递归回溯
- 为了便于运算,设+ 为0,- 为1,这样可以使用异或运算符表示符号三角形的关系:++为+即0^0=0, --为+即1^1=0, +-为-即0^1=1, -+为-即1^0=1
- 因为两种符号个数相同,可以对题解树剪枝; 当所有符号总数为奇数时无解,当某种符号超过总数一半时无解
public class fuhaosanjiao3 {
static int n;//第一行的符号个数
static int half;//n*(n+1)/2
static int count;//当前“+”或者“-”的个数
static int[][] p;//符号三角形矩阵
static long sum;//已找到的符号三角形的个数
//初始化及计算
public static float Compute(int nn) {
n = nn;
count = 0;
sum = 0;
half = (n*(n+1))/2;
if((half>>1)<<1 != half) {
return 0;
}
half = half>>1;
p = new int[n+1][n+1];
backtrack(1);
return sum;
}
public static void backtrack(int t) {
if(count>half || (t*(t-1)/2-count > half)){//对题解树的剪枝
return;
}
if(t>n) {
sum++;//符号三角形的总数目+1
}
else {
//每个位置都有两种情况0,1 ;0为正,1为负
for(int i = 0;i<2;i++) {
p[1][t] = i;
count += i;//对"-"个数进行计数,为了进行剪枝操作
//接下来绘制其余的n-1行
for(int j = 2;j<=t;j++) {
//通过异或的方式求其余行数的放置方式
p[j][t-j+1] = p[j-1][t-j+1]^p[j-1][t-j+2];
count += p[j][t-j+1]; //正好如果为1就加1
}
backtrack(t+1);
//恢复现场
for(int j = 2;j<=t;j++) {
count -= p[j][t-j+1];
}
count -= i;
}
}
}
public static void main(String[] args) {
// TODO Auto-generated method stub
float SUM = Compute(4);
System.out.print("总数: " + SUM);
}
}
7 n后问题
思路
- 解向量:x1,x2,x3...xn
- 显约束:xi=1,2.....n
- 隐约束:
-
- 不同列:xi != xj
- 不处于同一正,反对角线: abs(i-1) != abs(xi-xj)
- 用回溯法求解时,用完全n叉树表示解空间,用可行性约束减去不满足行,列,斜线约束的子树
//伪代码
private static boolean place(int k){
for(int j=1;j<k;j++){
if((Math.abs(k-j)==Math.abs(x[j]-x[k])) || (x[j]==x[k]))
return false;
}
return true;
}
private static void backtrack(int t){
if(t>n)
sum++;
else{
for(int i=1;i<=n;i++){
x[t]=i;
if(place(t))
backtrack(t+!);
}
}
}
8 图的m着色问题
问题
-
给定无向连通图G和m种不同的颜色。用这些颜色为图G的各顶点着色,每个顶点着一种颜色。是否有一种着色法使G中每条边的2个顶点着不同颜色
-
这个问题是图的m可着色判定问题。若一个图最少需要m种颜色才能使图中每条边连接的2个顶点着不同颜色,则称这个数m为该图的色数
-
求一个图的色数m的问题称为图的m可着色优化问题
思想
-
1将数组color[n]初始化为0
-
2 k=1
-
3 while(k>=1)
- 3.1 以此考察每一种颜色,若顶点k的着色与其他顶点的着色不发生冲突则转步骤3.2; 否则,搜索下一个颜色
- 3.2 若顶点已全部着色,则输出数组color[n],返回
- 3.3 否则
- 3.3.1 若顶点k是一个合法着色,则k=k+1,转步骤3处理下一个顶点
- 3.3.2 否则 重置顶点k的着色情况,k=k-1,转步骤3回溯
代码
public class test {
public static Set<String> set = new HashSet<String>();
public static int n, k, m, a, b, count = 0;
public static int[][] num;
public static int[] color;
public static boolean[] bool;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();//n个顶点
k = sc.nextInt();//k条边
m = sc.nextInt();//m种颜色
num = new int[n + 1][n + 1];
color = new int[n + 1];
bool = new boolean[m + 1];
for (int i = 0; i < k; i++) {//接下来的k行中,每行有2个正整数a,b; 表示图的一条边(a,b)
a = sc.nextInt();
b = sc.nextInt();
num[a][b] = num[b][a] = 1;
}
f(1, "");
System.out.println(count);
}
public static void f(int ren, String s) {
//顶点以及全部着色
if (ren == n + 1) {
set.add(s);
count++;
return;
}
for (int i = 1; i <= m; i++) {
if (!bool[i]) {
int boo = 0;
//检查颜色的可用性
for (int j = 1; j <= n; j++) {
if (num[ren][j] == 1 && i == color[j]) {
boo = 1;
break;
}
}
if (boo == 0) {//如果颜色可用
bool[i] = true;
color[ren] = i;
f(ren + 1, s + i);
color[ren] = 0;
bool[i] = false;
}
}
}
}
}
复杂度分析
-
用m种颜色着色n个顶点:m^n种可能的着色组合
-
图m可着色问题的解空间树中内结点个数是:∑(0 - n-1)(m ^ i)
-
对于每一个内结点,在最坏情况下,用判断颜色可用函数检查当前扩展结点的每一个儿子所相应的颜色可用性需耗时O(mn)。因此,回溯法总的时间耗费是:∑(0 - n-1)(m ^ i)(nm)= O(nm ^ n)
9 旅行商问题(TSP)
问题
- 某售货员要到若干城市去推销商品,已知各城市之间的路程(或旅费)。他要选定一条从驻地出发,经过每个城市一次,最后回到驻地的路线,使总的路程(或总旅费)最短(或最小)
思路
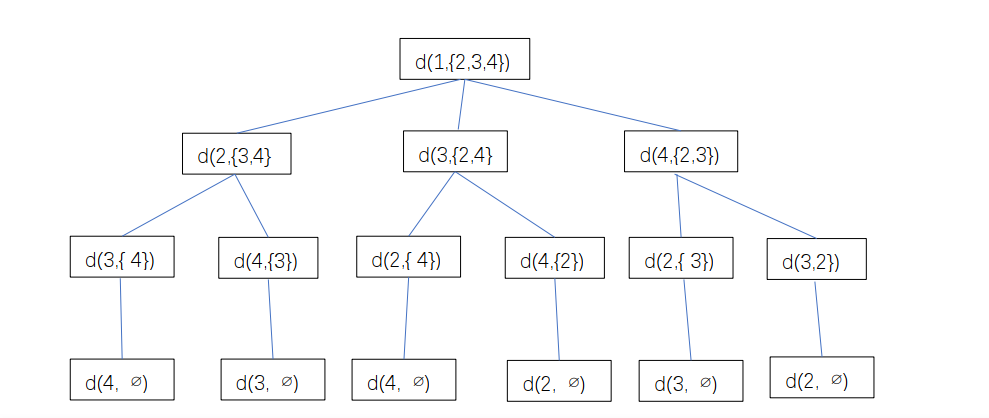
- 设G=(V, E)是一个带权图。图中各边的费用(权)为正数。图的一条周游路线是包括V中的每个顶点在内的一条回路。周游路线的费用是这条路线上所有边的费用之和。
旅行售货员问题是要在图G中找出费用最小的周游路线
代码
public class test {
static int n, m;//n城市数量,m边数量
static int grh[][];//地图
static int curentlength, bestlength;//当前距离,最短距离
static int curent[], best[];//当前路线,最好的路线
static int Max = Integer.MAX_VALUE;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();//城市数量
m = sc.nextInt();//边数量
grh = new int[n + 1][n + 1];
curent = new int[n + 1];
best = new int[n + 1];
curentlength = 0;
bestlength = -1;
for (int i = 1; i <= n; i++) {
curent[i] = i;
for (int j = 1; j <= n; j++) {
grh[i][j] = Max;//初始化地图,每个点之间的距离都是无穷大
}
}
for (int i = 1; i <= m; i++) {
int start = sc.nextInt();
int end = sc.nextInt();
int length = sc.nextInt();
grh[start][end] = length;
grh[end][start] = length;//把所有的边存储起来
}
backtrace(2);
if (bestlength != -1) {
for (int i = 1; i <= n; i++) {
System.out.print(best[i] + " ");
}
System.out.println("1");
System.out.println(bestlength);
} else {
System.out.println("-1");
}
}
private static void backtrace(int t) {
if (t == n) {
if (grh[curent[n - 1]][curent[n]] != Max && grh[curent[n]][1] != Max &&
(curentlength + grh[curent[n - 1]][curent[n]] + grh[curent[n]][1] < bestlength || bestlength == -1)) {
//1.当到准备去第n个城市的时候,首先要判断当前售货员与第n个点有没有路线,没有路线就剪掉
//2.要判断第n个点与起点1有没有路线,没有也要剪掉
//3.判断走完这条路线,回到原点的总距离是不是小于已经知道的最短距离,如果大于也剪掉 || 也有可能是第一个满足要求的还没有bestlength
//如果都符合,就要做更新操作
for (int i = 1; i <= n; i++) {
best[i] = curent[i];
}
bestlength = curentlength + grh[curent[n - 1]][curent[n]] + grh[curent[n]][1];
}
} else {
for (int i = t; i <= n; i++) {
if (grh[curent[t - 1]][curent[i]] < Max && (curentlength + grh[curent[t - 1]][curent[i]] < bestlength || bestlength == -1)) {
//上面的剪枝条件是,t-1表示现在售货员所在的城市,i表示他现在要准备去的城市,两者之间必须要有边
//bestlength=-1表示第一次走
//符合条件我们就需要交换
swap(t, i);//如果t和i一样就不用交换了 或者说交换完以后也是一样的
curentlength = curentlength + grh[curent[t - 1]][curent[t]];
backtrace(t + 1);
curentlength = curentlength - grh[curent[t - 1]][curent[t]];
swap(t, i);
}
}
}
}
private static void swap(int t, int i) {
int temp = 0;
temp = curent[t];
curent[t] = curent[i];
curent[i] = temp;
}
}
复杂度
- 算法backtrack在最坏情况下可能需要更新当前最优解O((n-1)!)次,每次更新bestlength需计算时间O(n),从而整个算法的计算时间复杂度为O(n!)
10 圆排列问题
问题
- 给定n个大小不等的圆c1,c2,…,cn,现要将这n个圆排进一个矩形框中,且要求各圆与矩形框的底边相切
- 圆排列问题要求从n个圆的所有排列中找出有最小长度的圆排列
- 比如:当n=3,且所给的3个圆的半径分别为1,1,2时,这3个圆的最小长度的圆排列如图所示
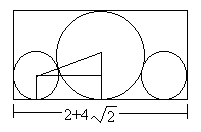
思想
- 圆排列问题的解空间是一棵排列树。按照回溯法搜索排列树的算法框架,设开始时a=[r1,r2,……rn]是所给的n个圆的半径,则相应的排列树由a[1:n]的所有排列构成
- center计算圆在当前圆排列中的横坐标*,由x^2 = sqrt((r1+r2)2-(r1-r2)2)推导出x = 2*sqrt(r1*r2)*
- Compute计算当前圆排列的长度。变量lenmin记录当前最小圆排列长度。数组r存储所有圆的半径。数组x则记录当前圆排列中各圆的圆心横坐标
- 在递归算法Backtrack中,当i>n时,算法搜索至叶节点,得到新的圆排列方案。此时算法调用Compute计算当前圆排列的长度,适时更新当前最优值。当i<n时,当前扩展节点位于排列树的i-1层。此时算法选择下一个要排列的圆,并计算相应的下界函数
伪代码
public void Backtrack(int t){
if (t>n)
Compute();
else{
for(int j=t;j<=n;j++){
swap(r[t],r[j]);
double centerx=Center(t);
if(centerx+r[t]+r[1]<min){//约束条件
x[t]=centerx;
Backtrack(t+1);
}
swap(r[t],r[j]);
}
}
}
//计算当前所选择圆的圆心坐标
public void Center(int t){
double b=0;
for(int j=1;j<t;j++){
double valuex=x[j]+2.0*sqrt(r[t]*r[j]);
if(valuex>temp)
temp=valuex;
}
retuen temp;
}
//计算当前圆排列的长度
public void Compute(){
double low=0;
double high=0;
for(int i=1;i<n;i++){
if(x[i]-r[i]<low)
low=x[i]-r[i];
if(x[i]+r[i]>hgih)
high=x[i]+r[i];
}
if(high-low<min)
min=high-low;
}
复杂度分析
- 由于算法backtrack在最坏情况下可能需要计算O(n!)次当前圆排列长度,每次计算需O(n)计算时间,从而整个算法的计算时间复杂性为O((n+1)!)
- 改进:例如,象1,2,…,n-1,n和n,n-1, …,2,1这种互为镜像的排列具有相同的圆排列长度,只计算一个就够了,可减少约一半的计算量。另一方面,如果所给的n个圆中有k个圆有相同的半径,则这k个圆产生的k!个完全相同的圆排列,只计算一个就够了。
分枝限界法
1 概述
分枝限界法与回溯法
- 相同点:分枝限界法类似于回溯法,是在问题的解空间树上搜索问题解的算法
- 不同点1:求解目标:回溯法的求解目标是找出解空间树中满足约束条件的所有解,而分枝限界法的求解目标则是找出满足约束条件的一个解,或是在满足约束条件的解中找出在某种意义下的最优解
- 不同点2:搜索方式的不同:回溯法以深度优先的方式搜索解空间树,而分枝限界法以广度优先或以最小耗费优先的方式搜索解空间树
基本思想
- 分枝限界法常以广度优先或以最小耗费(最大效益)优先的方式搜索问题的解空间树
- 在分枝限界法中,每一个活结点只有一次机会成为扩展结点。活结点一旦成为扩展结点,就一次性产生其所有儿子结点。在这些儿子结点中,导致不可行解或导致非最优解的儿子结点被舍弃,其余儿子结点被加入活结点表中
- 此后,从活结点表中取下一结点成为当前扩展结点,并重复上述结点扩展过程。这个过程一直持续到找到所需的解或活结点表为空时为止
2 常见的两种分枝限界法
队列式(FIFO)分枝限界法
- 按照队列先进先出(FIFO)原则选取下一个节点为扩展节点
优先队列式分枝限界法
- 按照优先队列中规定的优先级选取优先级最高的节点成为当前扩展节点
- 应用优先队列式分枝限界法求解具体问题时,应该根据具体问题的特点确定选用最大优先队列或者最小优先队列表示解空间的活结点表
3 01背包
问题
- 给定n种物品和一背包。物品i的体积是Si,其价值为Vi,背包的容量为C。问应如何选择装入背包的物品,使得装入背包中物品的总价值最大?
- 物品的个数n=3,背包容量C = 30, S =(16,15,15),价值W =(45,25,25)
队列式(FIFO)分枝限界法
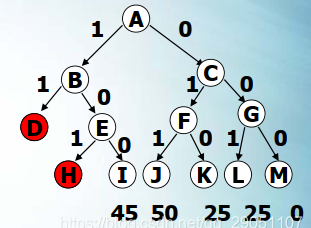
- 队列空 A→{A};
- A先进先出 →{B,C};
- B先进先出 →D,E;
- 由于D不合法,剔除;
- E入 →{C,E};
- C先进先出 →F,G →{E,F,G};
- E先进先出→H,I →{F,G,I};
- H不合法,剔除;
- F先进先出→J,K→{G,I,J,K};
- G先进先出→L,M→{I,J,K,L,M};
- 此时已到达叶子节点,计算各合法分支的值,最优值为50,对应的最优解为
优先队列式分枝限界法
- 在本例中,优先级即为各节点的价值,当前价值高的节点优先
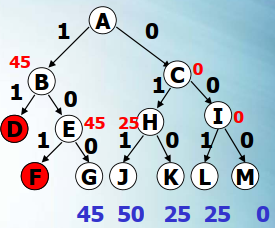
- 队列空 A→{A};
- A → B,C→{B,C};
- B的价值为45, C的价值为0, 则B出 →D,E;
- 由于D不合法,剔除;
- E入 →{C,E};
- E的价值大于C的价值,则 E出 →F,G →{C,F,G};
- 由于F不合法,剔除;
- 此时, G为叶子节点,则只能C出→H,I →{H,I};
- H的价值为25, I为0,则H出→J,K →{I,J,K};
- J,K均为叶子节点,则只能I出→L,M→{L,M};
- 此时各分支均已到达叶子节点,计算各合法分支的值,则最优值为50,最优解为{0,1,1}。
代码
//创建一个物品对象,封装重量、价值、单位重量价值三种属性
public class Knapsack implements Comparable<Knapsack> {
/** 物品重量 */
private int weight;
/** 物品价值 */
private int value;
/** 单位重量价值 */
private int unitValue;
public Knapsack(int weight, int value) {
this.weight = weight;
this.value = value;
this.unitValue = (weight == 0) ? 0 : value / weight;
}
public int getWeight() {
return weight;
}
public void setWeight(int weight) {
this.weight = weight;
}
public int getValue() {
return value;
}
public void setValue(int value) {
this.value = value;
}
public int getUnitValue() {
return unitValue;
}
@Override
public int compareTo(Knapsack snapsack) {
int value = snapsack.unitValue;
if (unitValue > value)
return 1;
if (unitValue < value)
return -1;
return 0;
}
}
// 按照分支限界算法将物品放入背包中\
public class FZXJProblem {
// 准备放入背包中的物品
private Knapsack[] bags;
// 背包的总承重
private int totalWeight;
// 给定的物品数
private int n;
// 物品放入背包可以获得的最大价值
private int bestValue;
public FZXJProblem(Knapsack[] bags, int totalWeight) {
super();
this.bags = bags;
this.totalWeight = totalWeight;
this.n = bags.length;
// 物品依据单位重量价值进行排序
Arrays.sort(bags, Collections.reverseOrder());
}
// 队列式分支限界法
public void solve() {
LinkedList<Node> nodeList = new LinkedList<Node>();
// 起始节点当前重量和当期价值均为0
nodeList.add(new Node(0, 0, 0));
while (!nodeList.isEmpty()) {
// 取出放入队列中的第一个节点
Node node = nodeList.pop();
if (node.upboundValue >= bestValue && node.index < n) {
// 左节点:该节点代表物品放入背包中,上个节点的价值+本次物品的价值为当前价值
int leftWeight = node.currWeight + bags[node.index].getWeight();
int leftValue = node.currValue + bags[node.index].getValue();
Node left = new Node(leftWeight, leftValue, node.index + 1);
// 放入当前物品后可以获得的价值上限
left.upboundValue = getUpboundValue(left);
// 当物品放入背包中左节点的判断条件为保证不超过背包的总承重
if (left.currWeight <= totalWeight
&& left.upboundValue > bestValue) {
// 将左节点添加到队列中
nodeList.add(left);
if (left.currValue > bestValue) {
// 物品放入背包不超重,且当前价值更大,则当前价值为最大价值
bestValue = left.currValue;
}
}
// 右节点:该节点表示物品不放入背包中,上个节点的价值为当前价值
Node right = new Node(node.currWeight, node.currValue,
node.index + 1);
// 不放入当前物品后可以获得的价值上限
right.upboundValue = getUpboundValue(right);
if (right.upboundValue >= bestValue) {
// 将右节点添加到队列中
nodeList.add(right);
}
}
}
}
// 当前操作的节点,放入物品或不放入物品
class Node {
// 当前放入物品的重量
private int currWeight;
// 当前放入物品的价值
private int currValue;
// 不放入当前物品可能得到的价值上限
private int upboundValue;
// 当前操作的索引
private int index;
public Node(int currWeight, int currValue, int index) {
this.currWeight = currWeight;
this.currValue = currValue;
this.index = index;
}
}
// 价值上限=节点现有价值+背包剩余容量*剩余物品的最大单位重量价值
// 当物品由单位重量的价值从大到小排列时,计算出的价值上限大于所有物品的总重量,否则小于物品的总重量
// 当放入背包的物品越来越来越多时,价值上限也越来越接近物品的真实总价值
private int getUpboundValue(Node n) {
// 获取背包剩余容量
int surplusWeight = totalWeight - n.currWeight;
int value = n.currValue;
int i = n.index;
while (i < this.n && bags[i].getWeight() <= surplusWeight) {
surplusWeight -= bags[i].getWeight();
value += bags[i].getValue();
i++;
}
// 当物品超重无法放入背包中时,可以通过背包剩余容量*下个物品单位重量的价值计算出物品的价值上限
if (i < this.n) {
value += bags[i].getUnitValue() * surplusWeight;
}
return value;
}
public int getBestValue() {
return bestValue;
}
}
//测试 结果为90
public class FZXJTest {
public static void main(String[] args) {
Knapsack[] bags = new Knapsack[] { new Knapsack(2, 13),
new Knapsack(1, 10), new Knapsack(3, 24), new Knapsack(2, 15),
new Knapsack(4, 28), new Knapsack(5, 33), new Knapsack(3, 20),
new Knapsack(1, 8) };
int totalWeight = 12;
FZXJProblem problem = new FZXJProblem(bags, totalWeight);
problem.solve();
System.out.println(problem.getBestValue());
}
}
4 装载问题
对列式分枝限界法
//分支限界法解装载问题
//装载问题先尽量将第一艘船装满
//队列式分支限界法,返回最优载重量
template<class Type>
Type MaxLoading(Type w[],Type c,int n)
{
//初始化数据
Queue<Type> Q; //保存活节点的队列
Q.Add(-1); //-1的标志是标识分层
int i=1; //i表示当前扩展节点所在的层数
Type Ew=0; //Ew表示当前扩展节点的重量
Type bestw=0; //bestw表示当前最优载重量
//搜索子集空间树
while(true)
{
//检查左儿子
Type wt=Ew+w[i]; //wt为左儿子节点的重量
if(wt<=c) //若装载之后不超过船体可承受范围
if(wt>bestw) //更新最优装载重量
{
bestw=wt;
if(i<n) Q.Add(wt); //将左儿子添加到队列
}
//将右儿子添加到队列
if(Ew+r>bestw&&i<n)
Q.Add(Ew);
Q.Delete(Ew); //取下一个节点为扩展节点并将重量保存在Ew
if(Ew==-1) //检查是否到了同层结束
{
if(Q.IsEmpty()) return bestw; //遍历完毕,返回最优值
Q.Add(-1); //添加分层标志
Q.Delete(Ew); //删除分层标志,进入下一层
i++;
r-=w[i]; //剩余集装箱重量
}
}
}
优先队列式分枝限界法
- 解装载问题的优先队列式分枝限界法用最大优先队列存储活结点表。活结点x在优先队列中的优先级定义为从根结点到结点x的路径所相应的载重量再加上剩余集装箱的重量之和
- 在优先队列式分枝限界法中,一旦有一个叶结点成为当前扩展结点,则可以断言该叶结点所相应的解即为最优解。此时可终止算法
搜索策略
1 概述
- 搜索:是指从问题出发寻找解的过程
- 通过搜索求解:在对问题进行形式化之后,现在需要对问题求解。一个解释一个行动序列,所以搜索算法的工作就是考虑各种可能的行动序列。可能的行动序列从搜索树中根节点的初始状态出发:第一步检测该结点是否为目标状态;进而考虑选择各种行动通过扩展当前状态完成;选择一条路往下走,把其他的选择暂且放一边,等以后发现第一个选择不能求出问题的解时再考虑
- 搜索树:根节点对应了初始状态;子节点对应了父节点的后继;节点显示状态,但对应的是到达这些状态的行动;对大多数问题,实际上不会构建整个树
- 无信息搜索策略
- 深度优先搜索(DFS)
- 广度优先搜索(BFS)
- 深度受限搜索(DLS)
- 迭代加速的深度优先搜索(IDS)
- 双向搜索(Bidirectional search)
2 深度受限搜索(DLS)
- 对深度优先搜索设置界限l
- 深度为l的结点当作没有后继对待
- 深度界限解决了无穷路径的问题,时间复杂度为O(bl),空间复杂度为O(bl)
- 深度优先搜索可以看作是特殊的深度受限搜索,其深度l为无穷大
3 迭代加速的深度优先搜索(IDS)
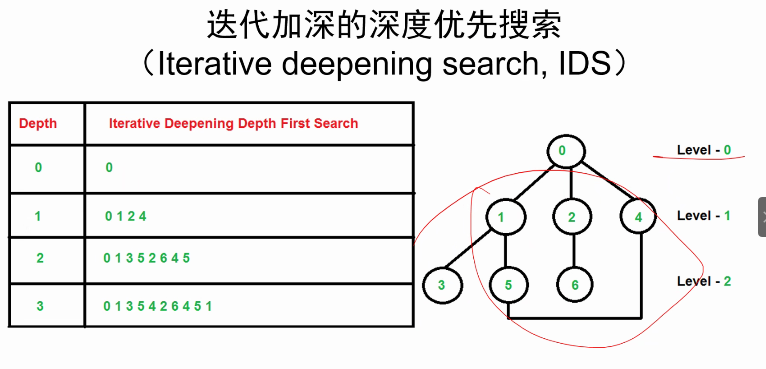
- 结合了DFS的空间优势与BFS的时间优势
- 会有浪费冗余吗?通常绝大多数的结点都在底层,所以上层的节点生产多次影响都不是很大
4 双向搜索
- 思路:同时运行两个策略,一个从初始状态向前搜索,同时另一个从目标状态向后搜索,希望它们在中间某点相遇,此时搜索中止
- 可以两个搜索是不同的,比如一个是深度优先,另一个是广度优先




 浙公网安备 33010602011771号
浙公网安备 33010602011771号