4动态规划
4动态规划
1 主要内容
- 动态规划的基本概念
- 动态规划的基本步骤
- 动态规划问题求解实例
2 动态规划基本概念
求解对象
- 最优化问题
- 工程问题中设计参数的选择
- 有限资源的合理分配
- 车间作业调度
- 交通系统的规划
- 等等
基本思想
- 与分治法类似,也是将问题分解为规模逐渐减小的同类型的子问题
- 与分治法不同,分解所得的子问题很多都是重复的
- 总体思想:保存已解决的子问题的答案,在需要时使用,从而避免大量重复计算
适合用动态规划求解的问题
- 若一个问题可以分解为若干个高度重复的子问题,且问题也具有最优子结构性质,就可以用动态规划法求解
- 具体方式:可以递推的方式逐层计算最优值并记录必要的信息,最后根据记录的信息构造最优解
解题步骤
- 找出最优解的性质,并刻画其结构特征
- 递归地定义最优值(写出动态规划方程)
- 以自底向上的递推方式计算出最优值
- 根据计算最优值时得到的信息,以递归方法构造一个最优解
3 实例之矩阵连乘问题
问题描述
- 对于给定的n个矩阵,M1,M2,…,Mn,其中矩阵Mi和Mj是可乘的,要求确定计算矩阵连乘积(M1M2…Mn)的计算次序,使得按照该次数计算矩阵连乘积时需要的乘法次数最少
- 设有矩阵M1,M2,M3,M4,其维数分别是:10×20,20×50,50×1,1×100,现要求出这4个矩阵相乘的结果,计算次序可以通过加括号的方式确定
思想一:动态规划之递归版本
- j-i种划分情况表示为通式:(Mi┅Mk)(Mk+1┅Mj)(i≤k<j)
- 记第t个矩阵Mt的列数为rt,并令r0为矩阵M1的行数,这两个矩阵相乘需要做r(i-1) × r(k) × r(j) 次乘法
- 由于已知(Mi┅Mk)和(Mk+1┅Mj)所需的最少乘法次数,记为m(i,k)和m(k+1,j),(Mi…Mk)(Mk+1…Mj)的矩阵连乘所需的最少乘法次数为:m(i,k)+m(k+1,j)+r(i-1)×r(k)×r(j)
- 对满足i≤k<j的共j-i种情况逐一进行比较,可得:m(ij)=min(i≤k<j)
public class JuZhenLianChen1 {
//1递归版本
//可以用数组p[0:n]来存放n个连乘矩阵的行数和列数(p[i-1]表示Ai的行数,p[i]表示Ai的列数);
private static int recurMatrixChain(int i,int j,int[] p) //最初始的矩阵连乘问题算法
{
if(i == j) return 0; //i == j,即只有一个矩阵,计算次数当然为零
int min = recurMatrixChain(i,i,p) + recurMatrixChain(i+1,j,p) + p[i-1] * p[i] * p[j];
for(int k = i + 1; k < j; k++){
int t = recurMatrixChain(i,k,p) + recurMatrixChain(k+1,j,p) + p[i-1] * p[k] * p[j];
if(t < min) min = t; //从k处断开,如果t比min更小,则说明存在更优的解决方法,把t赋值给min
}
return min;
}
public static void main(String[] args) {
int[] p = {5,3,4,2,7,5};
System.out.println(recurMatrixChain(1,5,p));//174
}
}
思想二:动态规划之填表法
- 跟以往的动态规划解题思路相同,要求A1~A5的连乘,就先求A1A2的,再求A1A2A3的…
我们需要填写下列这张表,它记录了每个子问题的值
![]()
- 按照上图的填写思路,我们最终填完所有的表
- 而下图的右侧表格代表的是括号的位置,比如我们在填(A1,A3)这格时,发现橙色的,也就是A1(A2A3)的乘法次数最少,所以我们把这个方案填入了下图的左表,此时括号是在A2前面,因此在右表填入2
- 注意这里A1A2也可以填1,同理A2A3也可以填2....
![]()
- 左表的(A1,A5)格就是我们要求的最少乘法次数,而根据右表,我们可以看出对应的连乘顺序。最终我们得出,最少乘法次数为174,顺序为:
(A1(A2A3))(A4A5)
public class JuZhenLianChen2 {
public static int getMinMultiplicationNum(int[] dims) {//若有n个矩阵,则数组维数设置为n+1
int n = dims.length-1;
int[][] tab_num = new int[n][n];//建表,存乘法次数
int[][] tab_split = new int[n][n];//建表,存括号位置
/*核心*/
for(int j=1;j<n;j++){//列,一列一列走
for(int i=j-1;i>=0;i--){//行
tab_num[i][j] = tab_num[i][j-1] + dims[i]*dims[j]*dims[j+1];//赋初值
tab_split[i][j] = j;
for(int k=i+1;k<j;k++){
if(tab_num[k][j] + tab_num[i][k-1] + dims[i]*dims[k]*dims[j+1] < tab_num[i][j]){
tab_num[i][j] = tab_num[k][j] + tab_num[i][k-1] + dims[i]*dims[k]*dims[j+1];
tab_split[i][j] = k;
}
}
}
}
trackback(tab_split,0,n-1);
System.out.println();
return tab_num[0][n-1];
}
//输出连乘顺序
private static void trackback(int[][] tab_split, int i, int j) {
if (i == j) {
System.out.print("A" + (i + 1));
} else {
System.out.print("(");
trackback(tab_split, i, tab_split[i][j] - 1);
trackback(tab_split, tab_split[i][j], j);
System.out.print(")");
}
}
public static void main(String[] args) {
int[] p = {5,3,4,2,7,5};
System.out.println(getMinMultiplicationNum(p));
}
}
4 实例之最长公共子序列问题(LCS)
问题
- 若Z<X,Z<Y,且不存在比Z更长的X和Y 的公共子序列,则称Z是X和Y 的最长公共子序列,记为Z∈LCS(X,Y),请注意,最长公共子序列往往不止一个
- 给定序列s1={1,3,4,5,6,7,7,8},s2={3,5,7,4,8,6,7,8,2},s1和s2的相同子序列,且该子序列的长度最长,即是LCS,s1和s2的其中一个最长公共子序列是
思路

public class LCS3 {
public static int findLCS(String A, int n, String B, int m) {
int[][] dp = new int[n + 1][m + 1];
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= m; j++) {
dp[i][j] = 0;
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (A.charAt(i - 1) == B.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = dp[i - 1][j] > dp[i][j - 1] ? dp[i - 1][j] : dp[i][j - 1];
}
}
}
return dp[n][m];
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
while (scanner.hasNextLine()) {
String str1 = scanner.nextLine().toLowerCase();
String str2 = scanner.nextLine().toLowerCase();
System.out.println(findLCS(str1, str1.length(), str2, str2.length()));
}
}
}
5 实例之子集合问题
问题
- 𝑆={𝑥𝑥1,𝑥𝑥2,…,𝑥𝑥𝑛𝑛}为正整数集合,c是一个正整数
- 子集和问题就是判断是否存在S的一个S1,使得S1中所有元素的和为c
代码
public class ZiJiHeWenTi4 {
static boolean isSubsetSum(int set[], int n, int sum)
{
//构建二维数组,行数是想求答案sum+1(第0行就是结果为0,方便计算),列数是第几个元素(注意这里0是不用元素的意思,所以需要数组下标+1)
boolean subset[][] = new boolean[sum+1][n+1];
//如果想求结果是0,那肯定返回ture
for (int i = 0; i <= n; i++)
subset[0][i] = true;
// 如果想求结果不是零,但不用元素,那肯定是false
for (int i = 1; i <= sum; i++)
subset[i][0] = false;
//填表
for (int i = 1; i <= sum; i++)
{
for (int j = 1; j <= n; j++)
{
subset[i][j] = subset[i][j-1];//一开始先默认和旁边那列一样
if (subset[i][j]==false && i >= set[j-1])//如果当前没找到(如果为true就不用找了)且当前结果是大于第j-1个元素,才有必要继续检索
subset[i][j] = subset[i - set[j-1]][j-1];//此处需要结合二维表思考
}
}
return subset[sum][n];
}
public static void main (String args[])
{
int set[] = {3, 34, 4, 12, 5, 2};
int sum = 1;
int n = set.length;
if (isSubsetSum(set, n, sum) == true)
System.out.println("找到子集合了!");
else
System.out.println("没找到子集合。");
}
}
6 最优二分搜索树
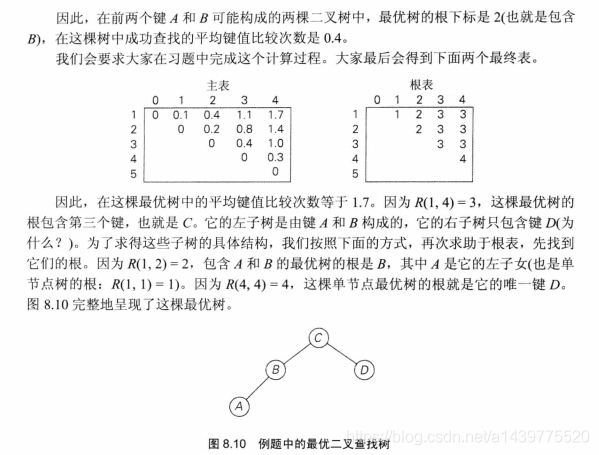
- 在二叉查找树基础上,引出了一个最优二叉查找树的问题:它在查找树中所有节点的平均键值比较次数是最低的。
- 当使用穷举法时,包含n个键的二叉查找树的总数量等于n个卡塔兰树,它已(4n)/(n1.5)的速度逼近无穷大
思路
- 我们设a1...an为从小到大排列的互不相等的键,p1...pn是它们的查找概率,T(i,j)是由键ai..aj构成的二叉树
- C(i,j)是在这棵树中成功查找的最小平均查找次数
- 当1<=i<=j<=n时,C(i,j)=MIN(i<=k<=j){C(i,k-1)+C(k+1,j)}+∑Ps(i<=s<=j)
- 且C(i,i-1)=0;C(i,i)=Pi

- 此处第五行并没什么实际意义 方便代码实现从数据下标0开始
public class ZuiYouErFenSouSuoShu5 {
/*
* 参数P:表示1~n个节点的查找概率。其中P[0] = 0,无意义
* 函数功能:返回在最优BST中查找的平均比较次数主表C[][],以及最优BST中子树的根表R
*/
public static void getBestTree(double[] P) {
int lenP = P.length;
double[][] C = new double[lenP+1][lenP]; //保存最优BST的成功查找的平均比较次数
int[][] R = new int[lenP+1][lenP]; //保存最优BST中子树的根表R
for(int i = 1;i < lenP;i++) {
C[i][i] = P[i];
R[i][i] = i;
}
for(int d = 1;d < lenP-1;d++) {
for(int i = 1;i < lenP-d;i++) {
int j = i + d;
double minval = Double.MAX_VALUE; //以double类型的最大值,表示minval趋向无穷大
int kmin = 0;
for(int k = i;k <= j;k++) {
if(C[i][k-1] + C[k+1][j] < minval) {
minval = C[i][k-1] + C[k+1][j];
kmin = k;
}
}
R[i][j] = kmin;
double sum = P[i];
for(int s = i+1;s <= j;s++)
sum += P[s];
C[i][j] = minval + sum;
}
}
System.out.println("在最优BST中查找的平均比较次数依次为:");
for(int i = 1;i < C.length;i++) {
for(int j = 0;j < C[0].length;j++)
System.out.printf("%.1f\t",C[i][j]);
System.out.println();
}
System.out.println("在最优BST中子树的根表R为:");
for(int i = 1;i < R.length;i++) {
for(int j = 0;j < R[0].length;j++)
System.out.print(R[i][j]+"\t");
System.out.println();
}
}
public static void main(String[] args) {
double[] P = {0,0.1,0.2,0.4,0.3};
getBestTree(P);
}
}
7 流水作业调度
问题
-
设有n个作业,每一个作业i均被分解为m项任务: T(i1), T(i2), ┅, T(im)(1≤i≤n,故共有n×m个任务),要把这些任务安排到m台机器上进行加工(总结:n个作业,m项任务,m台机器)
-
如果任务的安排满足下列3个条件,则称该安排为流水作业调度:
-
- 1每个作业i的第j项任务Tij(1≤i≤n, 1≤j≤m)只能安排在机器Pj上进行加工
- 2作业i的第j项任务Tij(1≤i≤n, 2≤j≤m)的开始加工时间均安排在第j-1项任务Ti,j-1加工完毕之后
- 3任何一台机器在任何一个时刻最多只能承担一项任务
-
最优流水作业调度:设任务Tij在机器Pj上进行加工需要的时间为tij,如果所有的tij(1≤i≤n, 1≤j≤m)均已给出,要找出一种安排任务的方法,使得完成这n个作业的加工时间为最少,这个安排称之为最优流水作业调度
-
注意点:优先调度(允许优先级较低的任务在执行过程中被中断,转而去执行优先级较高的任务);非优先调度(任何任务一旦开始加工,就不允许被中断,直到该任务被完成);流水作业调度一般均指的是非优先调度
-
当m=2时,该问题可有多项式时间的算法当机器数(或称工序数)m≥3时,流水作业调度问题是一个NP-hard问题;
m=2的流水作业调度
- n个作业{1,2,…,n}要在由2台机器M1和M2组成的流水线上完成加工。每个作业加工的顺序都是先在M1上加工,然后在M2上加工。M1和M2加工作业i所需的时间分别为ai和bi。流水作业调度问题要求确定这n个作业的最优加工顺序,使得从第一个作业在机器M1上开始加工,到最后一个作业在机器M2上加工完成所需的时间最少。
思想
-
直观上,一个最优调度应使机器M1没有空闲时间,且机器M2的空闲时间最少。在一般情况下,机器M2上会有机器空闲和作业积压2种情况。
最优调度应该是:
1. 使M1上的加工是无间断的。即M1上的加工时间是所有ai之和,但M2上不一定是bi之和。
2. 使作业在两台机器上的加工次序是完全相同的。
则得结论:仅需考虑在两台机上加工次序完全相同的调度。
设全部作业的集合为N={1,2,…,n}。S是N的作业子集。在一般情况下,机器M1开始加工S中作业时,机器M2还在加工其他作业,要等时间t后才可利用。将这种情况下完成S中作业所需的最短时间记为T(S,t)。流水作业调度问题的最优值为T(N,0)。
-
T(S,t)理解

- 最优子结构
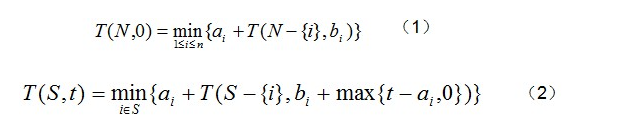
-
公式1理解:
-
- T(N,0)=min{ai + T(N-{i}, bi)}, i∈N
- ai:选一个作业i先加工,在M1的加工时间
- T(N-{i},bi}:剩下的作业要等bi时间后才能在M2上加工。注意这里函数的定义,因为一开始工作i是随机取的,M1加工完了ai之后,要开始加工bi了,这里M1是空闲的可以开始加工剩下的N-i个作业了,但此时M2开始加工bi,所以要等bi时间之后才能重新利用,对应到上面函数T(s,t)的定义的话,这里就应该表示成T(N-{i},bi), 所以最优解可表示为T(N,0)=min{ai + T(N-{i}, bi)}, i∈N,即我们要枚举所有的工作i,使这个式子取到最小值。
-
公式2理解:
-
- T(S,t)={ai + T(S-{i}, bi+max{t-ai,0})}, i∈S
- 其中:T(S-{i}, bi+max{t-ai,0}):剩下的作业等bi+max{t-ai,0}才能在M2加工,至于这里是怎么推导出来的呢?

补充之Johnson不等式
- 虽然满足最优子结构性质,也在一定程度满足子问题重叠性质。N的每个非空子集都计算一次,共2^n-1次,指数级的。为了解决这个问题引入Johnson不等式
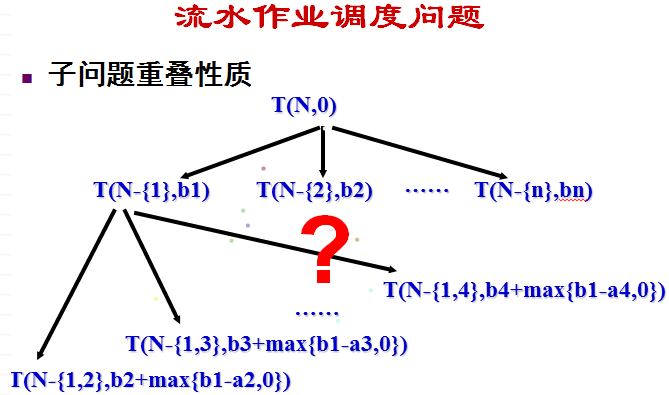
- Johnson不等式



动态规划思考
- 满足1.高度重复性 2.最优子结构性质时,一般采用动态规划法,但偶尔也可能得不到高效的算法
- 若问题本身不是NP-hard问题:进一步分析后就有可能获得效率较高的算法
- 若问题本身就是NP-hard问题:与其它的精确算法相比,动态规划法性能一般不算太坏,但有时需要对动态规划法作进一步的加工
8 备忘录方法
-
当某个问题可以用动态规划法求解,但二维数组中有相当一部分元素在整个计算中都不会被用到。因此,不需要以递推方式逐个计算二维数组中元素,而采用备忘录方法:数组中的元素只是在需要计算时才去计算,计算采用递归方式,值计算出来之后将其保存起来以备它用
-
若有大量的子问题无需求解时,用备忘录方法较省时;但当无需计算的子问题只有少部分或全部都要计算时,用递推方法比备忘录方法要好(如矩阵连乘,最优二分搜索树)
-
LSC的备忘录法
public class LCSBeiWangLu3 {
public static int f2(String arr1,String arr2,int n,int m) {
int[][] dp = new int[n + 1][m + 1];
if(n==0||m==0) {
return 0;
}else if(arr1.charAt(n-1)==arr2.charAt(m-1)) {
dp[n][m]=f2(arr1,arr2,n-1,m-1)+1;
}else {
dp[n][m]=Math.max(f2(arr1,arr2,n-1,m),f2(arr1,arr2,n,m-1));}
return dp[n][m];
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
String str1 = scanner.nextLine().toLowerCase();
String str2 = scanner.nextLine().toLowerCase();
System.out.println(f2(str1, str2,str1.length(), str2.length()));
}
}
9 最长递增子序列(LIS)
问题
- 假设A=<𝑎1,𝑎2,…,𝑎𝑛>为由n个不同的实数组成的序列,𝐴𝐴的递增子序列𝐿是这样的一个子序列:𝐿=<𝑎(𝑘1),𝑎(𝑘2),…,𝑎(𝑘𝑚)>,其中𝑘1< 𝑘2<…< 𝑘𝑚并且𝑎𝑘1<𝑎𝑘2<⋯<𝑎𝑘𝑚
- 最长递增子序列问题就是求𝐴的最长递增子序列,也就是说,需要求最大的𝑚值
- 例如, [2,3,7,101] 是数组 [10,9,2,5,3,7,101,18]的最长递增子序列
思路
- 思路一:将序列A排序好,变成B,然后和A做LCS就行
- 思路二:
public class LIS6 {
private static int getLargestLen(int[] array) {
int[] max = new int[array.length];
for (int i = 0; i <array.length ;="" i++)="" {="" max[i]="1;" }="" for="" (int="" i="1;" <="" array.length="" j="0;" j++)="" if="" (array[i]=""> array[j] && max[i] < max[j] + 1) {
max[i] = max[j] + 1;
}
}
}
int maxLen = 0;
for (int i = 0; i < array.length ; i++) {
if (maxLen < max[i]) {
maxLen = max[i];
}
}
return maxLen;
}
public static void main(String[] args) {
int[] ints = {1,5,2,3,4};
int largestLen = getLargestLen(ints);
System.out.println(largestLen);
}
}
10 SKI滑雪问题
- Michael 喜欢滑雪。为了获得速度,滑的区域必须向下倾斜,而且当你滑到坡底,不得不再次走上坡或者等付升降机来载你,Michael 想知道在一个区域中最长的滑坡。
- 区域由一个二维数组给出。数组的每个数字代表点的高度。当且仅当高度减小,一个人可以从某个点滑向上下左右相邻四个点之一。
public class ski7 {
private static int[][] arr; //存放输入的矩阵
private static int[][] value; //对应arr点的“滑雪长度”
private static int c; //arr的列数
private static int r; //arr的行数
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
while(sc.hasNext()){
r = sc.nextInt();
c = sc.nextInt();
int max = 0;
arr = new int[r][c];
value = new int[r][c];
for (int i = 0; i < r; i++) {
for (int j = 0; j < c; j++) {
arr[i][j] = sc.nextInt();
}
}
for (int i = 0; i < r; i++) {
for (int j = 0; j < c; j++) {
int temp = ski(i, j, Integer.MAX_VALUE);
if (temp > max) {
max = temp;
}
}
}
System.out.println(max);
}
sc.close();
}
/**
* @param col:arr的列数
* @param row:arr的行数
* @param maxValue:上一个arr点的值
* @return
*/
private static int ski(int row, int col, int maxValue) {
//出了矩阵的区域或者现在arr这个点的值大于上一个arr点的值,即跑到更高的点去了,无效,返回0
if (col >= c || col < 0 || row >= r || row < 0 || maxValue <= arr[row][col] ) {
return 0;
}
//若已经计算过了此arr点的“滑雪长度”,直接返回
if (value[row][col] > 0) {
return value[row][col];
}
//不然就计算此点的“滑雪长度” = 上下左右的点的“滑雪长度”的最大值 + 1
value[row][col] = max(ski(row-1, col, arr[row][col]), ski(row+1, col, arr[row][col]), ski(row, col-1, arr[row][col]), ski(row, col+1, arr[row][col])) + 1;
return value[row][col];
}
/**
* @param ski1
* @param ski2
* @param ski3
* @param ski4
* @return 最大值
*/
private static int max(int ski1, int ski2, int ski3, int ski4) {
return Math.max(Math.max(ski1, ski2), Math.max(ski3, ski4));
}
}
11 最大子段和问题
- 注意:当所有整数均为负整数时定义其最大子段和为0
- 例,(-2, 11, -4, 13, -5, -2)最大子段和为20
11.1暴力法(时间复杂度O(n^2))
public class ZuiDaZiDuanHe11 {
public static int maxSubSum1(int[] ints){
int[] sums = new int[ints.length];
int max=0;
for (int i=0;i<ints.length;i++){ int="" sum="0;" for="" (int="" j="i;j<ints.length;j++){" sum+="ints[j];" if="" (sum="">sums[i])
sums[i]=sum;
}
if (sums[i]>max){
max=sums[i];
}
}
return max;
}
public static void main(String[] args) {
int[] ints = {-2, 11, -4, 13, -5, 2};
System.out.println(maxSubSum1(ints));
}
}
11.2分治法(时间复杂度O(nlogn)
public static int maxSubSum2(int[] a,int l,int r){
if(l==r){
return a[l];
}
int mid = (l+r)/2;
int lsum = maxSubSum2(a,l,mid);//左区间
int rsum = maxSubSum2(a,mid+1,r);//右区间
int sum1=0,sum2=0;
int lefts=0,rights=0;
//注意这里一定要从右到左,不然不连续
for(int i=mid;i>=l;i--){
lefts+=a[i];
if(lefts>sum1){
sum1=lefts;
}
}
for(int i=mid+1;i<r;i++){ rights+="a[i];" if(rights="">sum2){
sum2=rights;
}
}
int msum=sum1+sum2;
return Math.max(Math.max(lsum,rsum),msum);
}
public static void main(String[] args) {
int[] ints = {-2, 11, -4, 13, -5, 2};
int maxSubSum1 = maxSubSum1(ints);
System.out.println(maxSubSum1);
int maxSubSum2 = maxSubSum2(ints, 0, 5);
System.out.println(maxSubSum2);
}
11.3动态规划法(时间复杂度O(n)
public static int maxSubSum3(int[] a){
int maxSum=0;//记录到当前为止的最大值
int temp=0;//中间变量,动态规划需要
for (int i=0;i<a.length;i++){ if="" (temp="">0)
temp+=a[i];
else
temp=a[i];
if(temp>maxSum)
maxSum=temp;
}
return maxSum;
}
public static void main(String[] args) {
int[] ints = {-2, 11, -4, 13, -5, 2};
int maxSubSum1 = maxSubSum1(ints);
System.out.println(maxSubSum1);
int maxSubSum2 = maxSubSum2(ints, 0, 5);
System.out.println(maxSubSum2);
int maxSubSum3 = maxSubSum3(ints);
System.out.println(maxSubSum3);
}
12 多边形问题
问题
-
多边形游戏是一个单人玩的游戏,开始时有一个由n个顶点构成的多边形,每个顶点被赋予一个整数值,每条边被赋予一个运算符“+”或“*”,所有边依次用整数从1到n编号‘
-
游戏第1步,将一条边删除
-
随后n-1步按以下方式操作:
-
- (1)选择一条边E以及由E连接着的2个顶点V1和V2
- (2)用一个新的顶点取代边E以及由E连接着的2个顶点V1和V2。将由顶点V1和V2的整数值通过边E上的运算得到的结果赋予新顶点
-
最后,所有边都被删除,游戏结束。游戏的得分就是所剩顶点上的整数值
-
问题:对于给定的多边形,计算最高得分
思路
- 设所给的多边形的顶点和边的顺时针序列为op[1],v[1],op[2],v[2],…,op[n],v[n]
- 在所给多边形中,从顶点i(1≤i≤n)开始,长度为j(链中有j个顶点)的顺时针链p(i,j) 可表示为v[i],op[i+1],…,v[i+j-1]
- 如果这条链的最后一次合并运算在op[i+s]处发生(1≤s≤j-1),则可在op[i+s]处将链分割为2个子链p(i,s)和p(i+s,j-s)
- 对于2个子链p(i,s)和p(i+s,j-s)
- 设m1是对子链p(i,s)的任意一种合并方式得到的值,而a和b分别是在所有可能的合并中得到的最小值和最大值
- 设m2是p(i+s,j-s)的任意一种合并方式得到的值,而c和d分别是在所有可能的合并中得到的最小值和最大值
- 根据上述定义有a≤m1≤b,c≤m2≤d
-
- (1)当op[i+s]='+'时,显然有a+c≤m≤b+d
- (2)当op[i+s]='*'时,有min{ac,ad,bc,bd}≤m≤max
- 因此,主链的最大值和最小值可由子链的最大值和最小值得到
- 可以根据上述分析递归求解
13 背包问题
13.1 0-1背包问题
- 给定n种物品和一背包。物品i的重量是wi,其价值为vi,背包的容量为C。问应如何选择装入背包的物品,使得装入背包中物品的总价值最大?
- 0-1背包问题是一个特殊的整数规划问题

public class BeiBao13 {
public static void getValue(int N,int W,int[] weight,int[]value) {
int sum[][]= new int[N+1][W+1];//sum[i][j]意思是:背包容量为j时,在前i件物品中取小于等于i件物品,此时取得的物品的价值最大
//注意下标问题
for(int i=1;i<=N;i++) {
for(int j=0;j<=W;j++) {
if(weight[i-1]>j) {//太重了,拿不了
sum[i][j]=sum[i-1][j];
}else {//拿:sum[i-1][j-weight[i]]+value[i] 不拿: sum[i-1][j]
//拿为什么是k-1? 因为sum[i-1][j-weight[i]]可以理解为此时还没拿第i件的最大价值,当然我们要留weight[i]空间
sum[i][j]=Math.max(sum[i-1][j-weight[i-1]]+value[i-1], sum[i-1][j]);
}
}
}
System.out.println(sum[N][W]);
}
public static void main(String[] args) {
int N=5;//物品有五件
int W=20;//背包容量为20
int[] weight = {2, 3, 4, 5, 9};//重量 2 3 4 5 9
int[] value = {3, 4, 5, 8, 10};//价值3 4 5 8 10
getValue(N,W,weight,value);
}
}
13.2完全背包
- 给出𝑛种物品和一个容量为𝑀的背包,每种物品都有无限件,物品𝑖重量为𝑤(𝑖),价值为𝑝(𝑖),其中𝑤(𝑖)>0,𝑝(𝑖)>0, 1<=𝑖<=𝑛
- 问将哪些物品装入背包可以使得背包中所放物品总重量不超过𝑀,并且背包中物品的价值总和达到最大
13.3多重背包问题
- 给出𝑛种物品和一个容量为𝑀的背包,物品𝑖重量为𝑤(𝑖),数量为𝑛um(𝑖),价值为𝑝(𝑖),其中𝑤(𝑖)>0, 𝑝(𝑖)>0, num(𝑖)>0, 1<=𝑖<=𝑛
- 问将哪些物品装入背包可以使得背包中所放物品总重量不超过𝑀,并且背包中物品的价值总和达到最大
13.4混合背包问题
- 在基本的0-1背包问题、完全背包和多重背包的基础上,将三者混合起来
- 也就是说有的物品只可以取一次或者不取(基本的0-1背包)
- 有的物品可以取无限次(完全背包)
- 有的物品可以取得次数有一个上限(多重背包)
13.5二维背包问题
- 二维费用的背包问题是指:对于每件物品,具有两种不同的费用;选择这件物品必须同时付出这两种代价
- 问怎样选择物品可以得到最大的价值
13.6分组背包问题
- 给出𝑛种物品和一个容量为𝑀的背包,每种物品都有无限件,物品𝑖重量为𝑤(𝑖),价值为𝑝(𝑖),其中𝑤(𝑖)>0,𝑝(𝑖)>0, 1<=𝑖<=𝑛。
- 这n个物品被划分为若干组,每组中的物品相互冲突,最多选一件放入背包
- 问将哪些物品装入背包可以使得背包中所放物品总重量不超过𝑀,并且背包中物品的价值总和达到最
13.7有依赖的背包问题
- 此类问题是基本的0-1背包问题的变形。与基本的0-1背包问题不同的是,物品之间存在某种“依赖”的关系
- 也就是说,如果物品𝑖依赖于物品𝑗,则表示如果要选物品𝑖,则必须先选物品𝑗
</a.length;i++){></r;i++){></ints.length;i++){></array.length></j;k++){></j)>





 浙公网安备 33010602011771号
浙公网安备 33010602011771号