一种多群体协作多级扰动引导粒子群优化算法（MCpPSO）

MCpPSO：A multi-swarm cooperative multistage perturbation guiding particle swarm optimizer

原文：https://www.sciencedirect.com/science/article/pii/S156849461400221X

1.摘要

在多群体信息共享和精英扰动引导思想的启发下，提出了一种新型的多群体协作多级扰动引导粒子群优化算法(MCpPSO)。 多群体信息共享的思想是通过不同进化机制的不同子群体之间的信息交流和共享，和谐地提高进化效率。 用从其他子群中获得的有益信息，有可能推动停滞的子群再一次恢复活力。多级精英扰动引导策略的目的是在保持精英学习机制的同时，在一定程度上降低全局最佳个体的学习速度和学习强度。它有效地扩大了探索领域，使粒子的飞行轨迹多样化。提出并分析了全局最佳粒子的中心位置摄动思想、中心位置的不同计算方法和重要参数的影响分析。 

2.介绍

每个粒子都具有“个体认知”和“社会认知”的能力。粒子群算法通过粒子群中粒子的协同作用来寻找最优解。

每一粒子的飞行速度由其个人最佳位置和整个粒子群找到的最佳位置迭代修正。

一种改进的算法是使用环邻域拓扑，不需要任何缝隙参数。它通过使用单个粒子的局部记忆来形成一个稳定的网络，保持最佳位置。

受多群信息共享和精英扰动引导思想的启发，本文提出了一种新型的粒子群优化算法MCpPSO，具有多群信息共享机制和多级全局扰动引导策略。在该算法中，以不同于传统粒子群算法的方式对飞行速度进行了更新。每个粒子都会根据自己的经验、子种群的最佳位置以及来自其他子种群的信息来更新自己。在进化过程中，通过对全局最优解进行扰动，使多样性增加。两种主要策略增加了跳出局部最优解的可能性，使粒子尽可能接近全局最优解。因此，该算法的综合性能有可能得到很大的提高。此外，此外，还讨论了全局最佳粒子中心位置的同步摄动运算、中心位置的不同计算模型和重要参数的影响分析。

3.相关知识

3.1 PSO，多群协作粒子群优化MCPSO

3.2 基于中心信息交换的多种群进化

当种群规模过小时，粒子群很容易被进化停滞所困。但是，种群规模过大会影响算法的收敛速度。因此很难决定不同问题的人口规模。根据这些观测资料，本文将大种群划分为几个独立演化的子种群。一方面，粒子可以像传统的PSO那样独立地寻找更好的解决方案。另一方面，他们也从其他的子群体中获取信息，这些子群体是独立进化的，并且彼此之间有着独特的进化信息。然后，进化信息被发送到其他子群，并指导对所有粒子的搜索。本文的信息共享机制以中心位置实现，该中心位置是子群中当前找到的最优解决方案的平均位置：

其中Q代表子群的数量。由于缺乏飞行速度，中心位置不会独立进化。因此，它被看作是一个虚拟粒子。

3.3 扰动粒子群算法

在粒子群算法中，粒子群在最优粒子群的中间附近迅速收敛。然而，如此高的收敛速度往往会导致：(1)多样性的丢失 (2)当gest粒子对应于局部最优时的早熟收敛。这推动了pPSA-a算法的发展一种基于扰动gest更新策略的扰动粒子群算法，该算法是基于可能性测度的概念对缺乏关于gest的真正最优性的信息进行建模。与常规方法不同，PPSA中的Gest表示为“可能是gbest的      。因此，粒子速度的计算可以重写为:

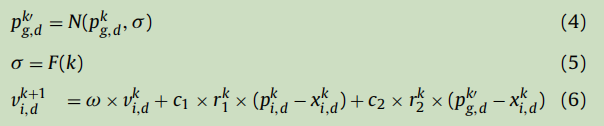
是k代后p-gbest的Dth维扰动操作。从(4)可以看出，p-gbest具有正态分布的特征。σ表示gbest的最优性的不确定性程度。为了说明随着时间的推移所收到的信息，减少了关于最佳位置的不确定性。σ被建模为一个不增加的函数，对于作为方程（7）的迭代次数。为了简单起见，F(k)定义为：

G是最大迭代次数，α是一个手动切换参数控制。

受干扰的全球最佳更新策略公式(4)-(6)应区别于常规的V的突变，即对全局最佳粒子进行随机扰动。p-gbest的功能是鼓励粒子探索超出搜索轨迹定义的区域。通过将与每个gbest相关的不确定性考虑为时间的函数，p-gbest在初期的提供了一个简单而有效勘探，在后期的时候鼓励局部微调。随后，该方法有助于降低早熟收敛的可能性，并引导搜索向有希望的搜索区域进行。

4.多群体协作多级扰动引导粒子群优化算法

勘探与开发的良好平衡对基于种群的随机优化算法的性能至关重要。基于多群信息共享机制和多阶段全局扰动导引搜索策略的思想，提出了一种新颖的多种群合作多级扰动导引粒子群优化器（MCpPSO）。多群体信息共享的思想是通过在具有不同进化机制的子群之间进行信息通信和共享来提高演化的效率。如果其他子群体停滞不前的话，就有可能再一次利用从其他子群体中学到的新信息来推动一些子群体的进化。多级扰动指导思想是在保留精英学习机制的同时，在一定程度上降低全局最优解的学习速度和学习强度。它扩大了精英社区周围的勘探领域，使粒子的飞行轨迹多样化。两种主要的策略增加了跳出局部最优的可能性。粒子法尽可能接近全局最优解。

4.1 多群信息通信与共享机制

多群共享操作将整个群划分为多个子群，彼此之间存在通信。由于子群在很大程度上是独立的，所以从 在初始解不同的情况下，该方法可以减少陷入与单群粒子群算法相同的局部最优解的可能性，并且有更大的机会找到真正的最优解。每个粒子都会根据自己的经验、子群的最佳粒子经验以及从其他子群中学到的指导信息来更新自己。多群协作粒子群算法用于中心信息共享的速度和位置更新方程如下：

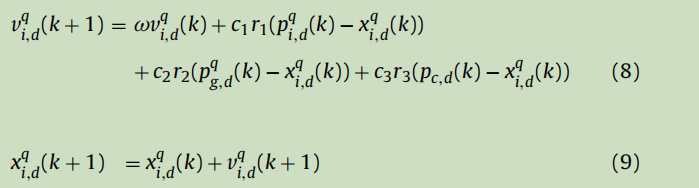
是第q个子种群第k代中粒子i的D维的速度，是第q个子种群第k代中粒子i的D维的值，是第q个子种群第k代中粒子i的个人最佳的D维，是第q个子种群的第k代中Gbest的D维。中心位置=之和的平均值（i=1,2,...，D）是周期k中从几个(全部？)子群中找到的最优解的平均位置。由公式三更新。c1是认知权重，c2是社会权重，c3是从其他子群体中学习的因素。r1、r2和r3是在[0,1]范围内均匀分布的三个随机数。

公式(8)的第一部分称为动量部分，表示单个粒子对其当前运动状态的置信度。它提供了必要的动力，并根据自己的经验进行惯性移动。第二部分是认知部分，它代表了粒子对其行为的思考，并鼓励粒子通过自己找到最佳位置。第三部分称为社会部分，代表了粒子群优化的精英学习过程，引导粒子向全局最优粒子学习。第四部分称为群通信部分，它代表了将粒子吸引到中心位置的中心信息共享机制。中心粒子的位置由几个子群最优位置的平均位置决定。这四个部分之间的相互促进和约束平衡共同决定了算法的性能。

同时，传统的PSO学习策略可能会导致“振荡”现象和“向前两步，一步后退”现象作为参考[35]进行分析。这很可能是由个人影响和邻域影响的线性总和引起的。因此，第四部分对问题进行了探讨。(8)当这种现象发生时，必须将粒子群拉出并修改方向。

4.2 三阶段全局扰动引导搜索策略

传统的扰动粒子群算法是基于公式(5)和(7)。p-gbest的固有功能是当σ在较高是在早期阶段提供一个简单而又有效的探索，在后期阶段σ较小鼓励局部微调。该策略在精英学习过程中有效地实现了当前群体的多样化。然而，在算法的最后阶段，它不符合全局最佳解的精确位置的收敛要求，在扰动半径很小的情况下，仍处于扰动状态。为此，提出了一种基于全局最优粒子的均匀合理扰动和收敛平衡的三阶段扰动导引策略。

三阶段扰动引导思想将算法的执行过程分为三个阶段。当扰动半径较大时，早期主要为多样化勘探。中间阶段当扰动半径减小时，主要集中在第一阶段发现的有前途的区域周围。最后阶段主要是针对最终解决方案的精确位置而无扰动。三阶段微扰导引思想在算法的相应阶段对种群搜索有不同的影响，这与迭代算法固有的搜索要求是一致的。这并不是说，随着越来越多的精英扰动过程被划分为更多的阶段，它会越来越好。

4.3 MCPPSO的主要操作

本文提出的策略对勘探和开采之间的不存在偏向。多群信息共享机制的主要思想是通过子群间的信息通信，在算法中加入种群多样性，加快搜索过程。 通过精英学习机制，特别是来自其他最佳的子群。三级扰动引导搜索策略有利于优化学习过程如公式(6)显示。同时，该操作使所有粒子的搜索轨迹多样化，即扩大了勘探范围。也就是说，我们提出的策略同时考虑了人口多样性和选择压力。文中给出了MCpPSO与两种策略杂交后的公式(10)-(12)和(9)。是“可能的全局最优位置”（扰动后的全局最优位置）。

对于搜索区域外的情况，采用了一个简单而流行的修复操作符，其工作原理如下（修正）：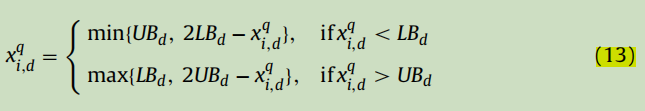

mcpPSO的流程图和主要操作如下：

5.关于MCpPSO的进一步思考

然而，进一步的问题值得考虑，公式(11)更关心的是。(1)更新当前子群粒子的速度时，对全局最优粒子(Gbest)进行扰动。如果人口的中心位置与gbest一起扰动会发生什么？(2)gbest在公式(11)第三项中对速度更新过程施加了引导作用。但是，GBEST仍然会通过公式(3)的中心位置影响速度更新过程。这些考虑的动机是进一步分析新提出的公式(8)更新策略不同的观点。

5. 1 中心位置扰动的影响

本节的目的是考虑中心位置的扰动操作的影响。当中心位置受到扰动时，MCpPSO的性能得到明显的改善吗？所以让中心位置同样受到三级扰动引导操作的扰动。然后，中心位置被扰动为方程(16)，并且方程(11)的速度更新操作将相应地修改为方程(17)。其他操作和参数保持不变，以将我们对MCPPSO的修改降至最低。将具有中心扰动的MCpPSO算法表示为MCpPSO+cp。

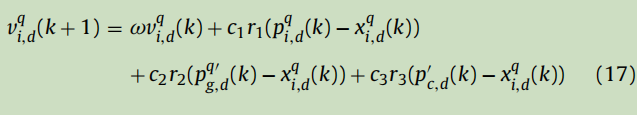
基于中心位置扰动的导引搜索策略对算法性能影响不大。

5.2 当前Gbest下对中心位置计算的影响

本小节的目的是考虑不同计算方法对中心位置的影响。也就是说，中心位置的速度更新公式(11)和计算公式(3)是否具有当前粒子所属的当前子群的全局最优粒子。结果表明，中心位置的计算公式(3)对算法的性能影响很小。 

5.3 亚群体数量的影响

6.个人总结

step0.初始化： 初始化种群Pop(t)，划分为Q个子种群，初始化中心位置；

step1.扰动： 对当前代的第q个子种群p-gbest进行扰动操作公式（10）；
step2.更新： 利用公式（11）进行更新速度以及公式（9）更新位置；

step3.越界处理： 用公式（13）进行处理；
step4.更新中心位置： 用公式（3）更新位置，作用是进行子种群信息共享机制，
中心位置是子群中当前找到的最优解决方案的平均位置;

step5.： 转步骤1。

对于公式（12）的三阶段全局扰动引导搜索：(1)防止种群多样性的丢失 (2)防止当过早收敛。
当扰动半径较大时，早期主要为多样化勘探。
中间阶段当扰动半径减小时，主要集中在前期发现的有前途的区域周围进行勘探。
最后阶段主要是针对最终解决方案的精确位置而无扰动。
三阶段微扰导引思想在算法的相应阶段对种群搜索有不同的影响，这与迭代算法原有的搜索要求是一致的。
这并不意味着，精英扰动过程划分为越来越多的阶段，效果会越来越好。

该算法利用
1.多群体协作分为Q个子种群用信息共享机制在子群之间的信息通信，将群体多样性添加到算法中。
同时，利用最优学习机制从子群的最优粒子中加速了全局最优解的搜索过程。
2.多级精英扰动引导策略的目的是在保持精英学习机制的同时，
在一定程度上降低全局最佳个体的学习速度和学习强度公式（12）。它有效地扩大了探索领域，
使粒子的飞行轨迹多样化。