如果你在世界杯赌球，第一次赌100，输了话第二次赌300，第三次900，直到赢了再从100开始，你觉得这样能赚到钱吗？

这个月在举行世界杯，发现朋友圈都是在秀赌球的东西，今天压的谁，赚了多少多少，或者是我压的少啦，错过了一套海景房之类的，看的我心里痒痒，然后我就按照这些赌徒的心态设计了一种赌的方法，因为是赌球所以胜率设置为三分之一，赔率1:2,，然后我就编码测试了一下，果然赌博还是算了。。。

 

世界杯赌球，第一次赌100，输了话第二次赌300，第三次900，直到赢了再从100开始
题目背景：
1、玩家遵循输了第二次赌资翻三倍，赢了赌资回归100
2、玩家有赌资一千万，可以全部用于赌
3、玩家没有第三方借钱渠道，每次的赌资都来自1000万中的累积的收益/亏损
4、玩家胜率为三分之一，赔率为1:2

 

#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#include<math.h>
#define N 1000 //测试的场数
#define n 1 //启动资金 （单位：百元）
#define money 100000 // 总资产一千万
#define m 3 //赔率
#define testtimes 3000//总测试次数

int main(){
    int i,wintimes=0,losetimes=0,temp,winsum=0,losesum=0; //赚钱的次数，亏钱的次数，赚钱数，亏钱数
    for(i=1;i<=testtimes;i++){
        printf("第%d次测试：",i);
        if(playonetime()>0){
            wintimes++;
            printf("赚了\n");

        }
        else{
            losetimes++;
            printf("破产了\n");
        }
    }
    
    printf("挣钱的次数为%d\n",wintimes);
    printf("破产的次数为%d\n",losetimes);
    printf("挣钱的概率%3.3f%%",(100*(float)wintimes/testtimes));

}
    
int playonetime(){  //单个玩家计算
    int sum = 0; //总收益
    int i,j,k,zhu=0;//次数；连续输的次数；单次胜负判定，当场的赌注
    for(i=0,j=0;i<N;i++){
        k=rand()%100+1; //产生1-100的随机数
        zhu = n*pow(m,j);
        if(zhu>=(money +sum)){
            break;
        }//单次赌注不能大于收益加总资金

        if(k<67){  //输了 输的概率为%67
            sum +=-n*pow(m,j);
            j++;
        }else{    //赢了
            sum +=n*pow(m,j);
            j=0;
        }
    }
    printf("共玩了%d场，最终收益为：%d(单位：百元) ：%d ",i,sum);
    return sum;
}

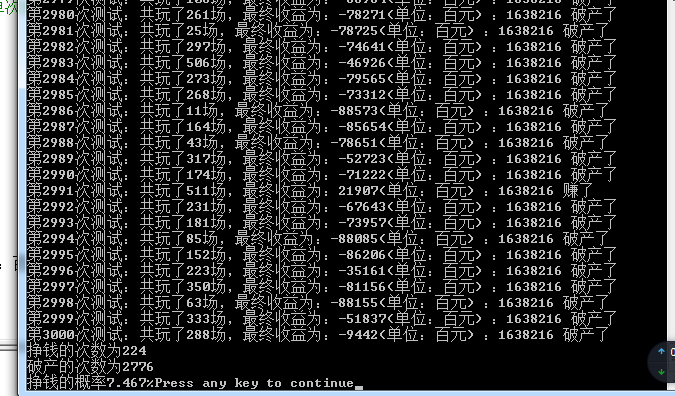
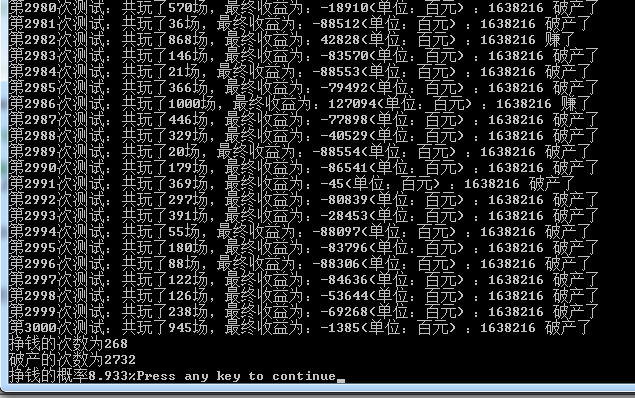
可以看到测试3000次能赚到钱的概率只有%7或%8，所以兄弟们，还是远离赌博吧，珍惜生命。哈哈！

 

补充：上面的程序只考虑到了当当前赌注大于资金时，就自动不赌了，这样不好，如果比较理性的话应该设当赚到了100万时就可以收手，看看这样赚钱的概率，我们先单独测试几次

#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#include<math.h>
#define N 1000 //测试的场数MAX
#define n 1 //启动资金 （单位：百元）
#define money 100000 // 总资产一千万
#define m 3//赔率
#define testtimes 1//总测试次数
    
int playonetime(){  //单个玩家计算
    int sum = 0; //总收益
    int i,j,k,zhu=0;//次数；连续输的次数；单次胜负判定，当场的赌注
    for(i=0,j=0;i<N;i++){
        k=rand()%100+1; //产生1-100的随机数
        zhu = n*pow(m,j);
        printf("第%d下注钱数为：%d  ",i+1,zhu);
        if(zhu>=(money +sum)||sum>10000){
            break;
        }//单次赌注不能大于收益加总资金

        if(k<67){  //输了 输的概率为%67
            sum-=zhu;
            j++;
            printf("收益为%d ",sum);
        }else{    //赢了
            sum +=zhu;
            j=0;
            printf("收益为%d ",sum);
        }
        printf("还剩下%d钱\n",money+sum);
    }
    printf("共玩了%d场，最终收益为：%d(单位：百元)  ",i,sum);
    return sum;
}

下面是二次测试下注的所有细节：

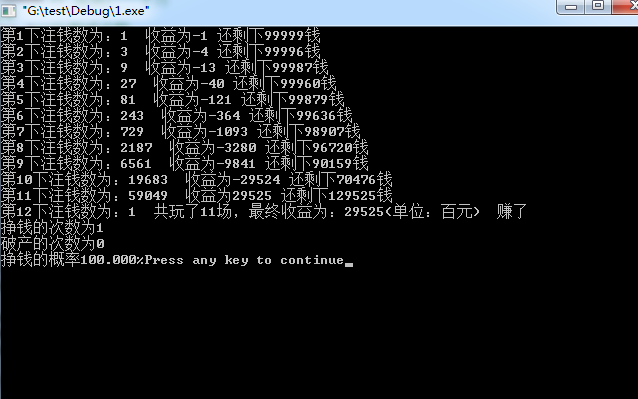
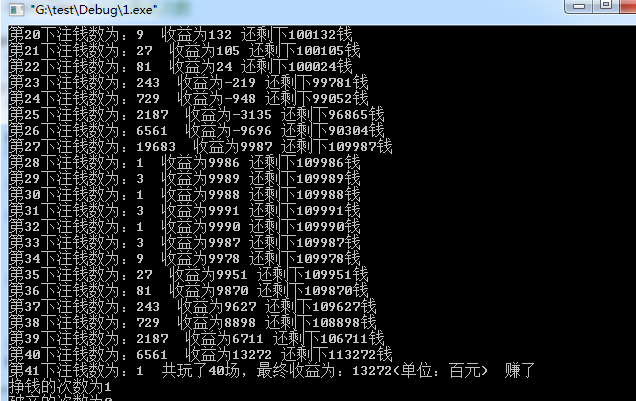
 上面是二次测试的具体压住细节。

 

下面我们看看如果测试200次，资产1000万，赚够100万就走了的话，有多大概率呢？

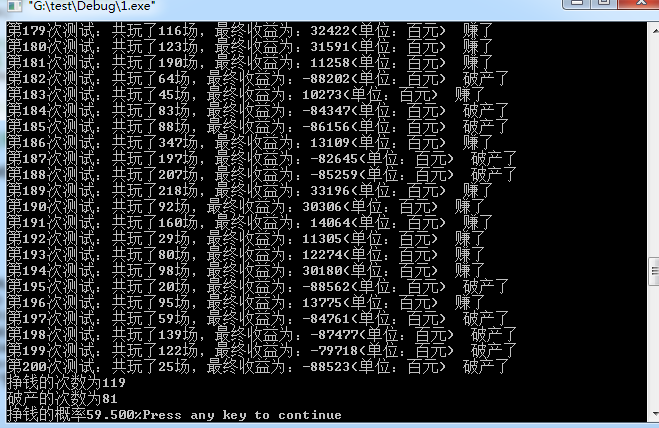
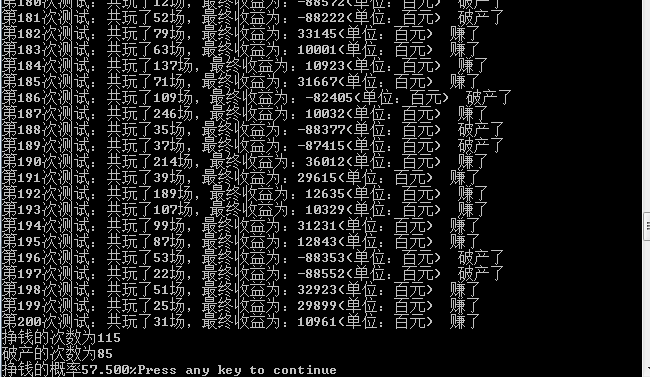
 然后我就发现概率竟然有50%-60%的概率，这么恐怖的吗？但是当我改变赌钱规则时，不再是输了100，再压300，输了再900，而是改了200,400，然后我就发现，胜率。。。

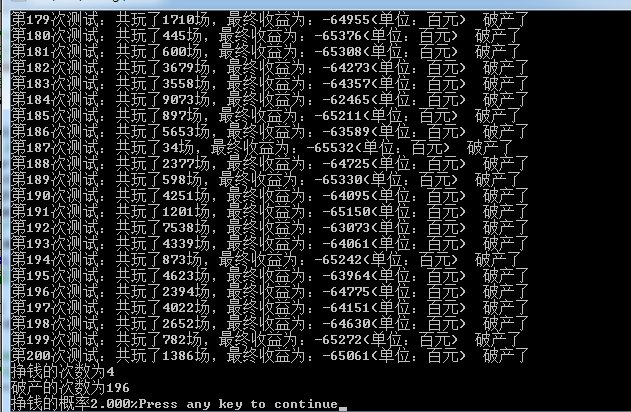
胜率变的极低，都是在2%左右甚至以下。之后我又改成翻4倍，5倍，4，5倍胜率在50%左右，到了6倍之后胜率就会明显下降。搞不懂，搞不懂，看来要学学数据建模分析了，根据自身的实际情况设计一个如何操作的模型，已达到最大化或者最大可能的收益，厉害，厉害。