树套树

参考：
1. 算法训练营6.4
简介：
1. 名称：树套树
2. 本质：一个节点为另一种树形结构（也可以是自己）的树形结构。
3. 一些abstract：我们用平衡树实现过查询过一棵树中的第k小，但是没有做到查询某一个区间的第k小，更不用说带动态修改的区间第k小了。如果不要求在线处理，cdq可以解决动态区间第k小，但是在线的话需要用树套树。
  
  树套树指在一个树形数据结构上，每个节点不再是一个节点，而是另一种树形结构，最常见的树套树有线段树套线段树、线段树套平衡树、树状数组套平衡树，尝试做到两个数据结构的功能的并集。
  
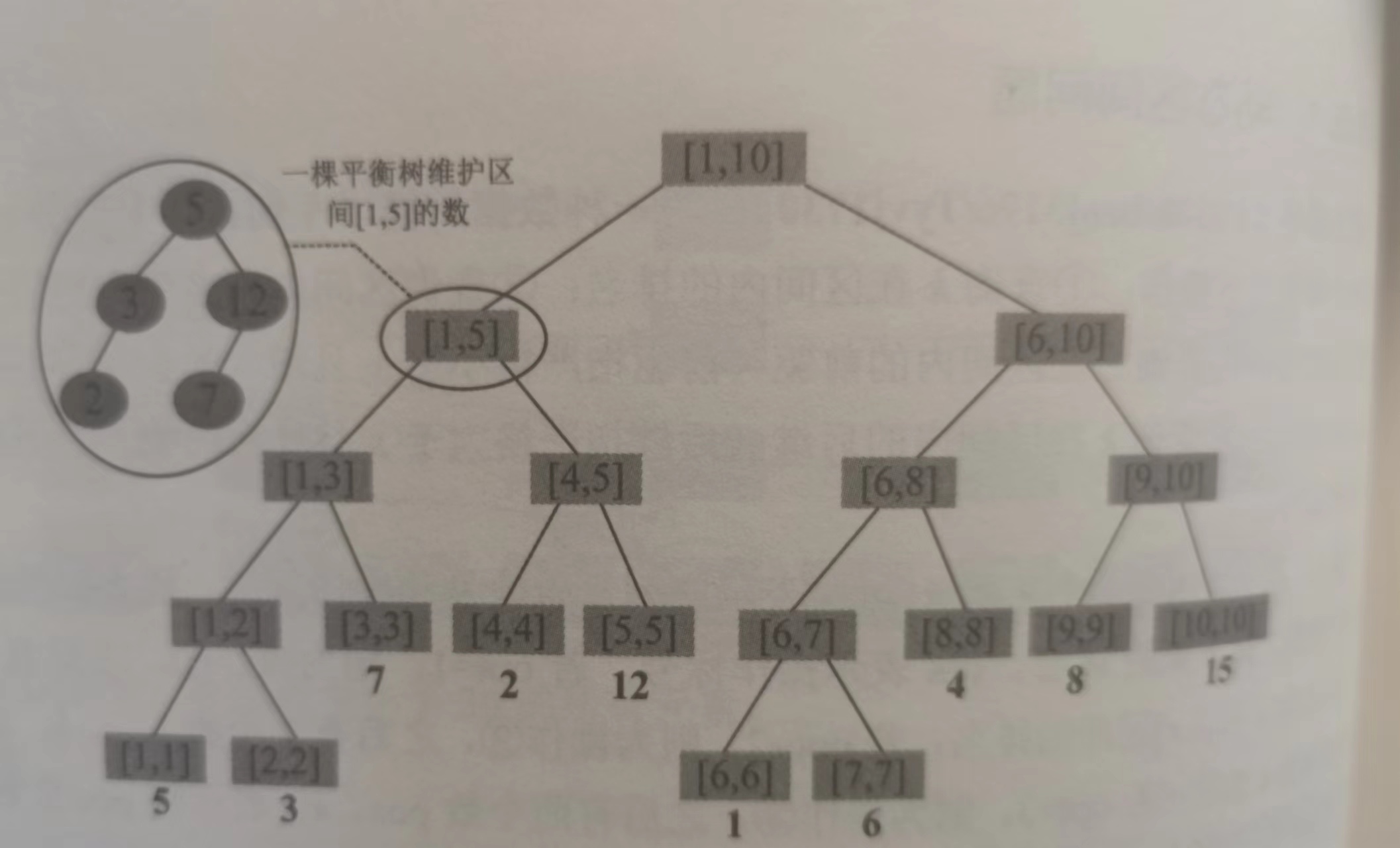
  以线段树套平衡树为例：线段树可以用来点、区间更新以及查询；平衡树可以用来查询第k小、排名、前驱和后继。我们用线段树维护区间，再用平衡树维护区间中的动态修改。先构造出线段树，每个线段树的节点除了记录左右边界，还用一棵平衡树维护这一个区间中的所有数，具体见例子，

例题：

（P3380/bzoj3196/Tyvj1730）要求维护一个有序数列，需要支持：

查询k在区间内的排名
查询区间内排名为k的值
修改某一个位置上的数值
查询k在区间内的前驱（最大的严格小于x的数，若不存在输出-2147483647）
查询k在区间内的后继（最小的严格大于x的数，若不存在输出2147483647）

区间操作和动态更新，所以可以用线段树+平衡树解决。

算法设计：

为线段树的每个节点都开辟一棵和区间大小相同的平衡树，平衡树一般用Treap或伸展树。线段树的每一层区间包含的元素个数都为n（因为每一层都是整个区间拆开的结果，然后每个节点都有一棵区间长度大小的平衡树，所以相当于又合了起来）。至多有logn层，于是所有的平衡树的节点总数是nlogn的。此树套树如图所示：

算法实现：

创建线段树和平衡树。

先创建线段树，然后每个节点的区间数据都插入该节点对应的平衡树中。

 void build(int x, int l, int r) {
   a[x].root = 0;
   for (int i = l; i <= r; i++) {
     a[x].insert(a[x].root, p[i]);
  }
   if (l == r) return;
   int mid = l + r >> 1;
   build(x << 1, l, mid);
   build(x << 1 | 1, mid + 1, r);
 }

查询k在[ql, qr]之间的排名（最后别忘了+1）：

在线段树中执行区间查询，把每个线段树节点中的平衡树中的排名加起来再加1就是最终排名。

 int queryrank(int x, int l, int r, int ql, int qr, int k) {  // 当前节点为x，其左右界限为[l, r]，查询区间为[ql, qr]，查询k的排名
   if(l > qr || r < ql) return 0;  // 不相交
   if (ql <= l && r <= qr) {  // 完全被查询包括
     return a[x].rank(a[x].root, k);  // 拿到[l, r]中比k小的个数
  }
   int ans = 0, mid = l + r >> 1;
   ans += queryrank(x << 1, l, mid, ql, qr, k);
   ans += queryrank(x << 1 | 1, mid + 1, r, ql, qr, k);
   return ans;
 }

线段树查询最多O(logn)层，平衡树查询最多O(logn)层，所以时间复杂度是O(loglog)的。

查询[ql, qr]区间排名为k的值。

区间内的元素是无序的，所以不能按区间查询排名。而用值进行二分搜索（初始l和r分别是总共的极小和极大值），每次查询这个值的排名，看看和k比较一下。

 int queryval(int ql, int qr, int k) {
   int l = min_val, r = max_val, ans = -1, rank;
   while(l <= r) {
     mid = l + r >> 1;
     rank = queryrank(1, 1, n, ql, qr, mid);
     if (rank + 1 <= k) {  // 如果排名已经为k，则还可以变大，l也是要mid + 1
       ans = mid;
       l = mid + 1;
    } else {
       r = mid - 1;
    }
  }
   return ans;
 }

复杂度为O(lognlognlog(max-min))。

点更新：

修改pos位置上的数为k。与线段树的点更新差不多，外加要更新每个节点对应的平衡树，最后修改p[pos] = k。

 void modify(int x, int l, int r, int pos, int k) {
   if (pos < l || pos > r) return;  // 不在这个范围内
   a[x].remove(a[x].root, p[pos]);  // 先删除这个值
   a[x].insert(a[x].root, k);  // 再插入新值
   if (l == r) return;
   int mid = l + r >> 1;
   modify(x << 1, l, mid, pos, k);
   modify(x << 1 | 1, mid + 1, r, pos, k);
 }

线段树中查询O(logn)层，删除和插入的复杂度为O(logn)，总复杂度为O(lognlogn)。

查询k在[ql, qr]区间的前驱：

若查询区间和当前节点的无交集，返回-inf；若查询区间覆盖了当前节点，则在当前节点平衡树中查找前驱；否则在左右子树中搜索，分别求前驱。

 int querypre(int x, int l, int r, int ql, int qr, int k) {
   if (l > qr || r < ql) return -inf;  // 不相交
   if (ql <= l && r <= qr) return a[x].pre(a[x].root, k);  // 完全覆盖在整个平衡树中查找前驱
   int mid = l + r >> 1;
   int ans = -inf;
   ans = max(ans, querypre(x << 1, l, mid, ql, qr, k));
   ans = max(ans, querypre(x << 1 | 1, mid + 1, r, ql, qr, k));
   return ans;
 }

线段树一共O(logn)层，查询复杂度也是O(logn)，所以总时间复杂度为O(lognlogn)。

查询k在[ql, qr]区间的后继：

基本同上：

 int querynxt(int x, int l, int r, int ql, int qr, int k) {
   if (l > qr || r < ql) return inf;  // 不相交
   if (ql <= l && r <= qr) return a[x].nxt(a[x].root, k);  // 完全覆盖在整个平衡树中查找后继
   int mid = l + r >> 1;
   int ans = inf;
   ans = min(ans, querynxt(x << 1, l, mid, ql, qr, k));
   ans = min(ans, querynxt(x << 1 | 1, mid + 1, r, ql, qr, k));
   return ans;
 }

总时间复杂度O(lognlogn)。

（POJ1195）矩形区域查询。二维的点更新和区间查询。因为只有点更新，所以之前用二维树状数组解决过，这里用线段树套线段树解决。

线段树一共有O(n)个节点，每个节点又有一个O(n)节点的线段树，所以空间复杂度为O(n^2)的。查询、更新操作总时间复杂度为O(lognlogn)的。

数据结构定义：创建一维线段树和二维线段树节点

 struct node_y {  // 第二维线段树节点，用来维护纵坐标的和
   int l, r;  // 纵坐标的区间
   int sum;  // 和值
 };
 
 struct node_x {  // 第一维线段树节点，维护二维区间的和
   int l, r;  // 横坐标的区间
   node_y s[maxn << 2];  // 第二维线段树
 }tr[maxn << 2];

创建树套树：不同于一维的，需要多一个参数，代表为哪个一维线段树节点创建二维线段树

 void build_y(int i, int l, int r, int k) {  // i为二维节点，代表[l, r]区间，k为一维线段树节点
   tr[k].s[i].l = l;
   tr[k].s[i].r = r;
   tr[k].s[i].sum = 0;  // 原题初始化就全是0
   if (l == r) return;
   int mid = l + r >> 1;
   build_y(i << 1, l, mid, k);
   build_y(i << 1 | 1, mid + 1, r, k);
 }
 
 void build_x(int i, int l1, int r1, int l2, int r2) {  // i为一维线段树节点，[l1, r1]是一维的范围，[l2, r2]是二维的范围，但这里[l2, r2]只能是[1, y_max]
   tr[i].l = l1;
   tr[i].r = r1;
   build_y(1, l2, r2, i);
   if (l1 == r1) return;
   int mid = l1 + r1 >> 1;
   build_x(i << 1, l, mid, l2, r2);
   build_x(i << 1 | 1, mid + 1, r, l2, r2);
 }

点更新：

 void update_y(int i, int y, int val, int k) {  // k是一维节点序号，i是二维节点序号 val是要加的值 y是要改的纵坐标
   tr[k].s[i].sum += val;
   if (tr[k].s[i].l == tr[k].s[i].r) return;
   int mid = (tr[k].s[i].l + tr[k].s[i].r) >> 1;
   if (y <= mid) update_y(i << 1, y, val, k);
   else update_y(i << 1 | 1, y, val, k);
 }
 
 void update_x(int k, int x, int y, int val) {  // k是一维节点序号，(x, y)是坐标，+val
   update_y(1, y, val, k);  // 对k节点的整棵树进行点更新
   if (tr[k].l == tr[k].r) return;
   int mid = tr[k].l + tr[k].r >> 1;
   if (x <= mid) update_x(k << 1, x, y, val);
   else update_x(k << 1 | 1, x, y, val);
 }

区间查询：

 int query_y(int i, int l, int r, int k) {
   if (tr[k].s[i].l == l && tr[k].s[i].r == r) return tr[k].s[i].sum;
   int mid = (tr[k].s[i].l + tr[k].s[i].r) >> 1;
   if (r <= mid) return query_y(i << 1, l, r, k);
   else if (l > mid) return query_y(i << 1 | 1, l, r, k);
   else return query_y(i << 1, l, mid, k) + query_y(i << 1 | 1, mid + 1, r, k);
 }
 
 int query_x(int k, int l1, int r1, int l2, int r2) {  // 查询区间[l1, r1][l2, r2]
   if (tr[k].l == l1 && tr[k].r == r1) return query_y(1, l2, r2, k);
   int mid = tr[k].l + tr[k].r >> 1;
   if (r1 <= mid) return query_x(k << 1, l1, r2, l2, r2);
   else if (l > mid) return query_x(i << 1 | 1, l1, r2, l2, r2);
   else return query_x(k << 1, l1, r2, l2, r2) + query_x(i << 1 | 1, l1, r2, l2, r2);
 }

（HDU4819）点更新 & 区间查询（最大值和最小值）

所有二维的最小值的最小值是一维的最小值，所以可以树套树。

数据结构定义：

 struct node {
   int Max, Min;
 }tr[maxn << 1][maxn << 1];  // 第i维就是处理i维坐标

建树：

 void pushup_x(int i, int k) {  // 1-i2-k
   tr[k][i].Max = max(tr[k << 1][i].Max, tr[k << 1 | 1][i].Max);
   tr[k][i].Min = min(tr[k << 1][i].Min, tr[k << 1 | 1][i].Min);
 }
 
 void pushup_y(int i, int k) {  // 1-i2-k
 tr[k][i].Max = max(tr[k][i << 1].Max, tr[k][i << 1 | 1].Max);
   tr[k][i].Min = min(tr[k][i << 1].Min, tr[k][i << 1 | 1].Min);
 }
 
 void build_y(int i, int k, int l, int r, int flag) {  // i第二维坐标；k第一维坐标；处理第二维的[l, r]；flag == 1代表横坐标区间已经是一个点了，此时不用管儿子，flag == 2表示横坐标仍然是一个区间，这时要根据儿子的答案取父亲的答案
   int mid, val;
   if (l == r) {
     if (flag == 1) {
       scanf("%d", &val);
     tr[k][i].Max = tr[k][i].Min = val;
    } else {
       pushup_x(i, k);
    }
     return;
  }
   mid = (l + r) >> 1;
   build_y(i << 1, k, l, mid, flag);
   build_y(i << 1 | 1, k, mid + 1, r, flag);
 }
 
 void build_x(int k, int l, int r) {
   if (l == r) {
     build_y(1, k, 1, n, 1);  // 整棵树都要建，已经为叶子节点，flag == 1
     return;
  }
   int mid = l + r >> 1;
   // 一方面处理更小的竖着的矩形
   build_x(k << 1, l, mid);
   build_x(k << 1 | 1, mid + 1, r);
   // 另一方面处理这个竖着的矩形。
   build_y(1, k, 1, n, 2);
 }

区间查询：

 // 查询[xa, ya] < [xb, yb]
 
 void query_y(int i, int k, int l, int r, int l2, int r2) {  // 查询第二维线段树，[l2, r2]，当前是[l, r]
   if (l2 <= l && r <= r2) {
     Max = max(Max, tr[k][i].Max);
     Min = min(Min, tr[k][i].Min);
     return;
  }
   int mid = l + r >> 1;
   if (l2 <= mid) query_y(i << 1, k, l, mid, l2, r2);
   if (mid < r2) query_y(i << 1 | 1, k, mid + 1, r, l2, r2);
 }
 
 
 void query_x(int k, int l, int r, int l1, int r1) {  // 查询第一维线段树，[l1, r1]，当前是[l, r]
   if (l1 <= l && r <= r1) {
     query_y(1, k, 1, n, ya, yb);
     return;
  }
   int mid = l + r >> 1;
   if (l1 <= mid) query_x(i << 1, l, mid, l1, r1);
   if (mid < r1) query_x(i << 1 | 1, mid + 1, r, l1, r1);
 }

点更新：

 void modify_y(int i, int k, int l, int r, int val, int flag) {
   if (l == r) {
     if (flag == 1) tr[k][i].Max = tr[k][i].Min = val;
     else {
       pushup_x(i, k);
    }
     return;
  }
   int mid = l + r >> 1;
   if (mid >= y) modify_y(i << 1, k, l, mid, val, flag);
   else modify_y(i << 1 | 1, k, mid + 1, r, val, flag);
   pushup_y(i, k);
 }
 
 void modify_x(int k, int l, int r, int val) {
   if (l == r) {
     modify_y(1, k, 1, n, val, 1);
     return;
  }
   int mid = l + r >> 1;
   if (mid >= x) modify_x(k << 1, l, mid, val);
   else modify_x(k << 1 | 1, mid + 1, r, val);
   modify_y(1, k, 1, n, val, 2);
 }

posted on 2022-05-15 11:34 小染子阅读(617) 评论(1) 收藏举报