SBT
-
-
简介:
-
名称:SBT(Size Balanced Tree,节点大小平衡树)。
-
本质:是一种自平衡二叉查找树,通过旋转来保证子树的大小大致相等来保持平衡,更容易实现。在O(logn)时间内完成所有二叉搜索树的相关操作。
-
一些abstract:和普通的二叉搜索树相比,SBT仅加入了简洁的核心操作maintain。因为SBT用来保持平衡的是size域,所以当查询操作比较多的时候,因为节点的期望高度接近,SBT会有优势。另外,SBT保存的子树大小可以用来查询第k大,而AVL,Treap,红黑树存储的额外信息不能用来查询第k大。其中SBT的高度是O(logn)的,维护操作均摊下来是O(1)的,其余主要操作复杂度是O(logn)的。
-
-
操作:
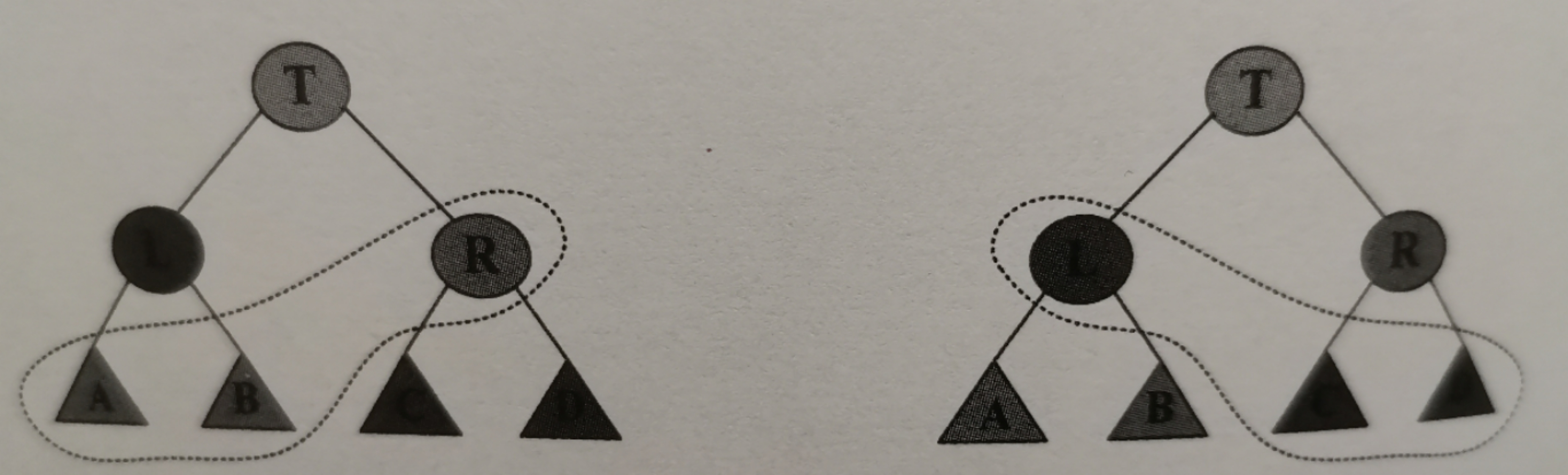
概括一下就是叔叔的子树大小一定大于侄子的子树大小,如图1所示:
![]()
带虚线的部分要保证上子树size大于下子树size。
板子:
#include<algorithm> #include<cstdio> #include<cstring> using namespace std; const int N=100100;int M; struct ss{ int key[N], size[N], left[N], right[N], count[N]; int rt, nodecnt; void clear(){ rt=0,nodecnt=0; memset(key,0,sizeof(key)); memset(s,0,sizeof(s)); memset(left,0,sizeof(left)); memset(right,0,sizeof(right)); memset(count,0,sizeof(count)); } void z_x(int &p){ // 左旋 int k=right[p]; right[p]=left[k];left[k]=p; size[k]=size[p]; size[p]=size[right[p]]+size[left[p]]+count[p]; p=k; } void y_x(int &p){ // 右旋 int k=left[p]; left[p]=right[k];right[k]=p; size[k]=size[p]; size[p]=size[right[p]]+size[left[p]]+count[p]; p=k; } void peace(int &p, bool flag){ if (!p) return; if(!flag) { // 加到了左子树 if(size[left[left[p]]] > size[right[p]]) y_x(p); else { // 加到了左子树的右子树 if (size[right[left[p]]]>size[right[p]]) { z_x(left[p]);y_x(p); } else return; } } else { // 加到右子树 if (size[right[right[p]]] > size[left[p]]) z_x(p); else { if (size[left[right[p]]]>size[left[p]]){ y_x(right[p]);z_x(p); } else return; } } peace(left[p],false); peace(right[p],true); peace(p,true); peace(p,false); } void insert(int &p,int x){ // 在根p的子树中,加入一个值为x的数 if(!p){ // 没出现过 p=++nodecnt; if (nodecnt == 1) rt = 1; key[p]=x; size[p]=count[p]=1; return; } size[p]++; if (x < key[p]) insert(left[p],x); else if (x > key[p]) insert(right[p],x); else { count[p]++; return; } peace(p,x > key[p]); } void remove(int &p, int val, int type) { // 删除一个值为val的数 type为0是正常减少一个,type为1是全部删除 if (!p) return; size[p]--; if (key[p] == val) { if (count[p] > 1 && type == 0) { // 必须删一个且大于一个的情况才可以直接返回 count[p]--; return; } if (!left[p] || !right[p]) { // 有一个为空,则直接用不为空的儿子代替这个节点 p = left[p] + right[p]; } else { // 先令直接后继代替此点,然后删除直接后继 int tmp = right[p]; while(left[tmp]) { tmp = left[tmp]; } key[p] = key[tmp]; count[p] = count[tmp]; remove(right[p], key[tmp], 1); // 必须全部删掉 } } else if (val < key[p]) remove(left[p], val, type); // 继承删除的方法 else remove(right[p], val, type); } int find_v(int &p, int val) { // 根据val在p子树中查找 if (!p || key[p] == val) return p; // 确定没找到或者找到 if (val < key[p]) return find_v(left[p], val); else return find_v(right[p], val); } int getMin() { if (!rt) return -inf; int p = rt; while(left[p]) p = left[p]; return key[p]; } int getMax() { if (!rt) return inf; int p = rt; while(right[p]) p = right[p]; return key[p]; } int rank(int &p, int val) { // val的排名 if(!p) return 1; int tmp=0; if(val <= key[p]) tmp = rank(left[p], val); else tmp = size[left[p]] + count[p] + rank(right[p], val); return tmp; } int select(int &p, int x){ // 第x小的数 if(x >= size[left[p]] + 1 && x <= size[left[p]] + count[p]) return key[p]; if(x <= size[left[p]]) return select(left[p], x); else return select(right[p], x - count[p] - size[left[p]]); } int getPre(int &p, int q, int val) { // 求val在子树p中的前驱 q记录了之前找到的答案位置 if (!p) return key[q]; if (key[p] < val) { return getPre(right[p], p, val); // p的值不够,尝试往大了找,说明q可以更好,更新为p。然后q就放小于val的p的位置,防止找过头 } return getPre(left[p], q, val); // p的值够了,得往小了找,q保持原状,不能超过val } int getNxt(int &p, int q, int val) { // 求val在子树p中的后继 q记录了之前找到的答案位置 if (!p) return key[q]; if (key[p] > val) { return getNxt(left[p], p, val); // p的值够了,尝试往小了找,说明q可以更好,更新为p。然后q就放大于val的p的位置,防止找过头 } return getNxt(right[p], q, val); // p的值不够,得往大了找,q保持原状,不能小于等于val } }T; int main(){ T.clear();scanf("%d",&M); int &rt=T.rt=0; while(M--){ int opt,x;scanf("%d%d",&opt,&x); if(opt==1) T.insert(rt,x); else if(opt==2) T.remove(rt, x); else if(opt==3) printf("%d\n",T.rank(rt,x)); else if(opt==4) printf("%d\n",T.select(rt,x)); else if(opt==5) printf("%d\n",T.getPre(rt, rt, x)); else if(opt==6) printf("%d\n",T.getNxt(rt, rt, x)); } return 0; }