分块
-
-
算法训练营第二章
-
-
-
名称:分块。
-
本质:优化后的暴力。
-
一些abstract:
设sn = 根号n。
树状数组和线段树维护的信息必须满足信息合并特性,即对于区间来说,分成两个区间分别操作和单独对一个区间的操作是一样的。不满足这个特性,则不能使用树状数组和线段树。
分块几乎可以解决所有区间更新和区间查询问题,但是效率差一些。分块算法就是把所有数据分成若干块,维护块内信息,使得块内查询为O(1)时间,总查询为O(sn)。
设数据是连续的n个,通常我们将数据分成sn块,前面的块大小都是sn,最后一块可能不足这个值,也无所谓。pos[i]表示位置i所属的块号。对每个块都进行信息维护(暴力/懒标记)(懒标记用来存整个区间都进行的操作,只有不是整个区间的操作时才处理懒标记),分块可以解决如下问题:
-
单点更新:所属区间懒标记下传,暴力更新,复杂度O(sn)。
-
区间更新:对于待修区间横跨的整个块,打上懒标记即可,显然只有两侧的块可能打不了,则下传二者懒标记,再暴力修改覆盖部分的值。因为整个块的数量不超过sn,并且暴力修改的部分的长度小于2sn,下传懒标记也是暴力改,所以下传的操作数小于2sn,下传完再直接修改不完整的部分,操作数也小于2sn,所以总共要进行的操作小于5sn,复杂度O(sn)。
-
区间查询:和区间更新类似,也是整个块的用块存储的信息统计答案,两端不完整的块就暴力扫描,时间复杂度同上,为O(sn)。
-
-
-
操作:
-
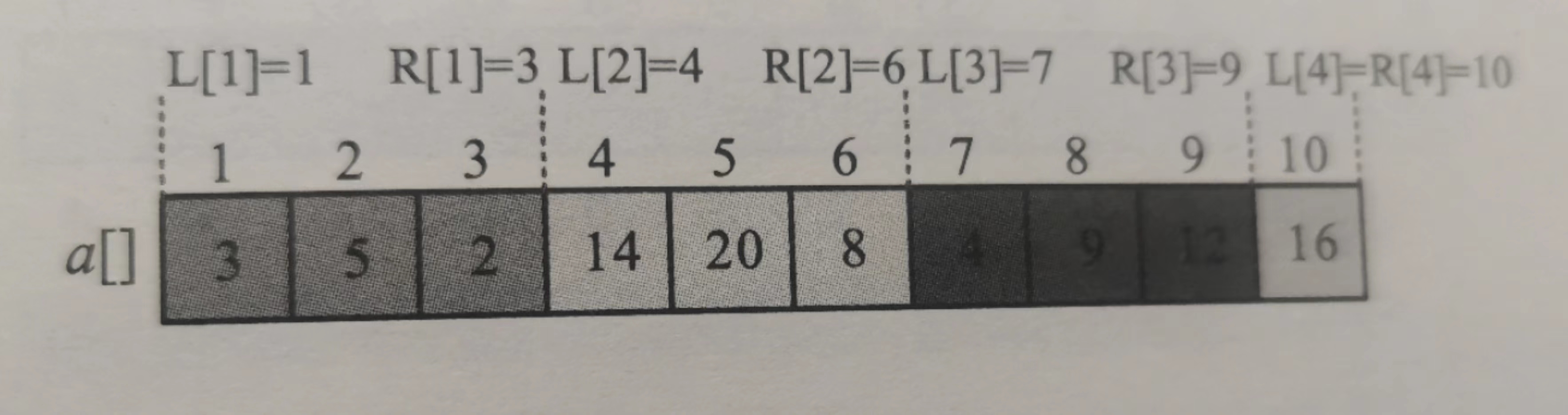
预处理:将序列分块,每个块都标记左右端点的下标,存到L[i],R[i]中,对最后一个块,要单独赋值它的R[i]。分块结果如下:
![]()
R[4] = n = 10
int t = (int)(sqrt(n * 1.0)), num = n / t;
if (n % num) num++; // 一共n个,分成了num块,每一个块大小为t
for (int i = 1; i <= num; i++) {
L[i] = (i-1)*t + 1; // 第i块的起点
R[i] = i * t; // 第i块的终点
}
R[num] = n; // 最后一块越界了,需要改回来这里以维护区间和为例:
// sum[i]表示第i块的和,a存原始数据,pos[i]表示第i个数据属于pos[i]块
for (int i = 1; i <= num; i++) {
for (int j = L[i]; j <= R[i]; j++) {
pos[j] = i;
sum[i] += a[j];
}
} -
区间更新:比如将区间[l, r]区间的元素都加d(假设r不小于l)。
先求出l和r所属的块:
int p = pos[l], q = pos[r];分类讨论:如果同属一块,则直接暴力修改:(这里因为只有加,懒标记只有一种,所以不用先下放懒标记,不然先后顺序需要注意一下,比如有一个乘法的懒标记,再进行加操作,就得先下放乘法的懒标记,再执行这次的加法)
if (p == q) {
for (int i = l; i<= r; i++) {
a[i] += d;
}
sum[p] += 1ll * (r - l + 1);
}不属于同一块,则对中间完全覆盖的块打上懒标记,暴力修改不完整的两个小块:
else {
add[i] += d;
for (int i = p + 1; i <= q - 1; i++) {
add[i] += d; // 对中间完全覆盖的块打上懒标记
}
// 暴力修改不完整的两个小块
for (int i = l; i <= R[p]; i++) {
a[i] += d;
}
sum[p] += 1ll * d * (R[p] - l + 1);
for (int i = L[q]; i <= r; i++) {
a[i] += d;
}
sum[q] += 1ll * d * (r - L[q] + 1);
} -
区间查询:查询[l, r]区间的元素和。
先求出l和r所属的块:
int p = pos[l], q = pos[r];
long long ans = 0;分类讨论:如果同属一块,则直接暴力累加,再加上懒标记上的值。
if (p == q) {
for (int i = l; i<= r; i++) {
ans += a[i];
}
ans += 1ll * add[p] * (r - l + 1);
}不属于同一块,则对中间完全覆盖的块打上懒标记,暴力修改不完整的两个小块:
else {
for (int i = p + 1; i <= q - 1; i++) {
ans += sum[i] + 1ll * add[i] * (R[i] - L[i] + 1); // 对中间完全覆盖的块打上懒标记
}
// 暴力修改不完整的两个小块
for (int i = l; i <= R[p]; i++) {
ans += a[i];
}
ans += 1ll * add[p] * (R[p] - l + 1);
for (int i = L[q]; i <= r; i++) {
ans += a[i];
}
sum[q] += 1ll * add[q] * (r - L[q] + 1);
}
printf("%lld", ans);
-
-
例题:
-
(HDU5057)给出一个数组,有两个操作:
-
单点修改某个位置的值
-
区间查询[l, r],指出这个区间中从低往高数第p位为q的个数是多少
给n个数,m个操作(都是十万级别)。对于每个查询,给出答案。
考虑分块,先预处理最开始的每个区间的每个位的不同的值的数量,这个复杂度是O(10nlog(int))级别的。
对于查询操作,只需要O(sn)级别。
对于修改操作,暴力修改即可,是O(1)级别。
-
-