线段树
-
-
算法训练营
-
-
简介:
-
名称:线段树(Segment Tree)
-
本质:维护区间信息(信息需要满足结合律,就是(a+b)+c=a+(b+c)的那种性质),对于点、区间更新、区间查询的复杂度均为O(logn)。
-
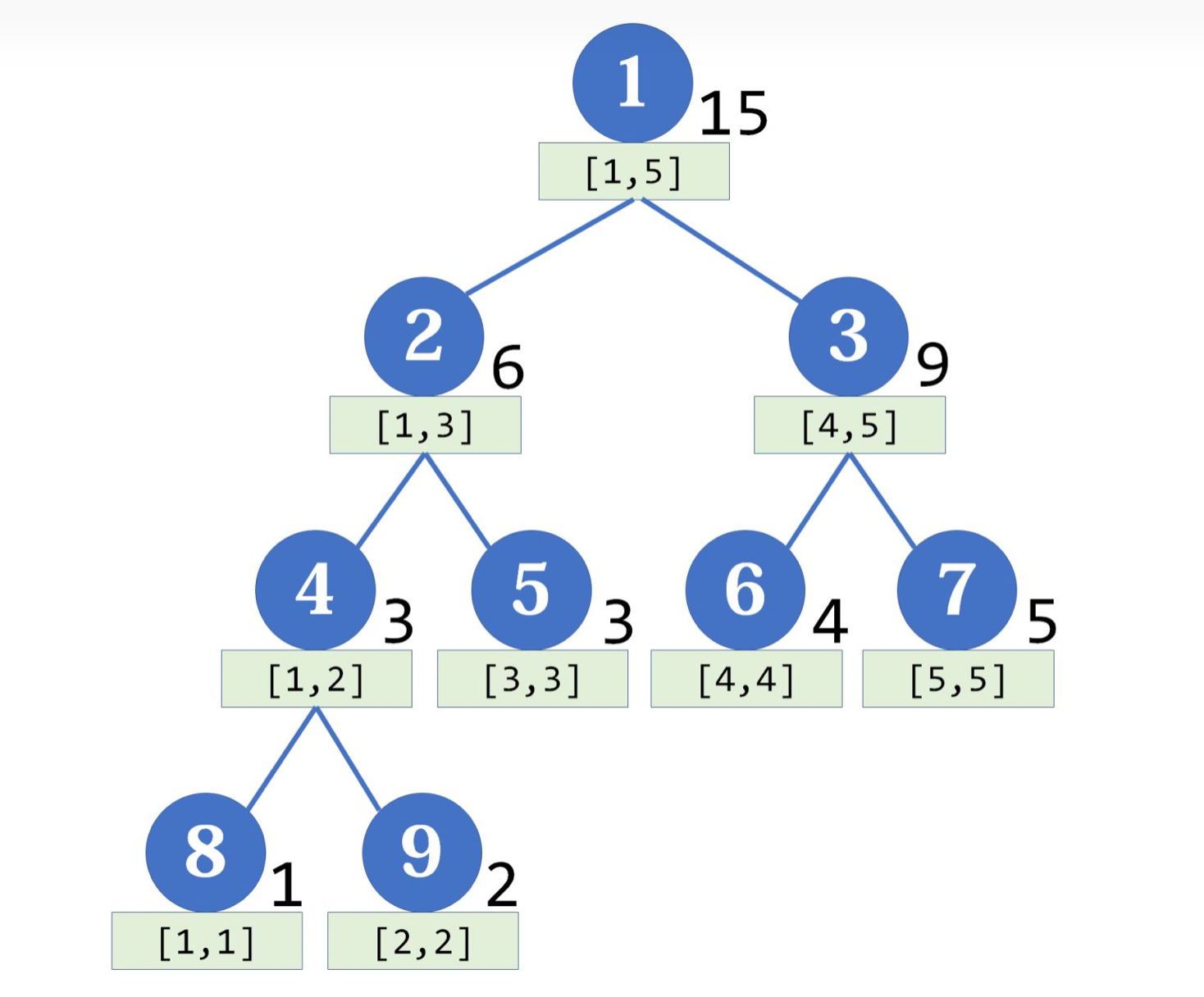
一些abstract:线段树是一棵平衡二叉树,每个节点代表一个区间内的值,以区间和为例。母节点比如代表[l, r]的和,左儿子就是[l, l+mid]的和,右儿子就是[l+mid+1, r]的和。线段树比树状数组可以多实现O(logn)的区间修改,支持区间加、乘等,更具通用性,也就是说能用树状数组解决的问题都可以用线段树解决,但是树状数组节省空间,代码易懂,运行常数小,所以二者各有千秋。
![]()
-
-
操作:以最简单的区间最大值为例:
-
创建Build:lc为左儿子,rc为右儿子。显然要递归建树,根据儿子的结果得到父亲的结果
板子:
-
点更新update:现在将a[i]修改为v,显然也是先改叶子节点,然后一步步往上修改到根节点。
板子:
void update(int k, int i, int v) { // 将a[i]更新为v
if (tree[k].l == tree[k].r && tree[k].l == i) { // 有一说一后面的部分纯属扯淡,因为i大于建树的n应该直接特判出来,所以后面那个默认是承认的
tree[i].ans = v;
return;
}
int mid = (tree[k].l + tree[k].r) / 2;
if (i <= mid) update(lc, i, v); // 划分到左子树中
else update(rc, i, v); // 划分到右子树中
tree[k].ans = max(tree[lc].ans, tree[rc].ans); // 得到了儿子们的答案,
} -
区间查询:查询[l, r]区间的最值,显然不会有刚刚好的区间让你去查询,看起来得按照建的树,分成若干个小线段,逐步渗透到叶子节点,比如刚才的树中,如果查询[2, 4]的最值,因为在3这个位置就已经裂开了,所以显然要分成[2, 3], [4]两个子线段,然后把[2, 3]下放到左子树,[4]下放到右子树。左子树中因为2这个位置会裂开,所以又得分成[2]和[3]分别送到叶子节点,右侧的[4]也送到叶子节点,然后得到答案之后取个max就行了。
板子:
int query(int k, int l, int r) { // 求[l, r]区间的最值,l和r在整个查询过程中是一定的,改变的是k,而k对应了线段树中的左右区间
if (tree[k].l >= l && tree[k].r <= r) { // 直接包括了整个k代表的区间,所以要返回k的max
return tree[k].ans;
}
int mid = (tree[k].l + tree[k].r) / 2;
int Max = -inf;
if (l <= mid) { // 涉及到左子树的答案,递归查询
Max = max(Max, query(lc, l, r));
}
if (r > mid) { // 涉及到右子树的答案,递归查询
Max = max(Max, query(rc, l, r));
}
return Max;
}
上面的都是简单的操作,下面开始上硬菜了。
-
区间更新:将[l, r]区间的所有元素都更新为v。注意这里只是更新,没有查询,所以引入了“懒操作”的概念,就是不查的时候不改,查了再说,颇像赶ddl的我x。
这里以将[l, r]区间的所有元素都更新为v为例,做法是这样的:
-
若当前节点的区间,被区间[l, r]覆盖,则更新并打上懒标记,表示此节点已经被更新,但是儿子还没有更新!!!然后不继续递归下去!!!
-
当查询的时候,如果发现这个节点有懒标记,则将懒标记下传到子节点,同时自己节点的懒标记清除,将子节点更新并做懒标记,继续查询,如果覆盖了含有懒标记的区间,就不用再递归了,只有查询区间是懒标记区间的一部分的时候,才继续下传懒标记,更新子节点。
-
更新操作递归回去的时候更新路径上的答案。
板子:
void lazy(int k, int v) { // 更新k区间的答案,并打上懒标记
tree[k].ans = v;
tree[k].lz = v;
}
void pushdown(int k) { // 向下传递懒标记
lazy(lc, tree[k].lz); // 下传给左子节点
lazy(rc, tree[k].lz); // 下传给右子节点
tree[k].lz = -inf; // 清除自己的懒标记
}
void update(int k, int l, int r, int v) { // 在k节点对应的区间,执行区间[l, r]上的更新v
if (tree[k].l >= l && tree[k].r <= r) {
lazy(k, v); // 被覆盖了,那就打上懒标记跑路~
return;
}
// 没被覆盖
// 有懒标记,则需要下放懒标记
if(tree[k].lz != inf) {
pushdown(k);
}
int mid = (tree[k].l+tree[k].r) / 2;
if (l <= mid) { // 涉及到左子树了
update(lc, l, r, v); // 在左子树中更新
}
if (r > mid) { // 涉及到右子树了
update(rc, l, r, v); // 在右子树中更新
}
tree[k].ans = max(tree[lc].ans, tree[rc].ans); // 更新自己的答案
} -
-
区间查询(修改):
带上区间更新之后,我们需要处理带懒标记的区间查询。
板子:
int query(int k, int l, int r) { // 当前在k节点,查询[l, r]区间的答案
if (tree[k].l >= l && tree[k].r <= r) { // 如果区间被覆盖,直接返回答案
return tree[k].ans;
}
// 这里注意,有人可能会问如果当前区间是打上懒标记的节点的儿子怎么办,看起来儿子还没更新不是吗。
// 注意到递归到儿子了,也就是一定经过了父亲,而经过父亲之后,必然会把懒标记下放并更新儿子,所以是没问题的。
if (tree[k].lz != inf) { // 有懒标记,下放!
pushdown(k);
}
int mid = (tree[k].l + tree[k].r) / 2, Max = -inf;
if (l <= mid) {
Max = max(Max, query(lc, l, r));
}
if (r > mid) {
Max = max(Max, query(rc, l, r));
}
return Max;
}
-
-
注意事项:
-
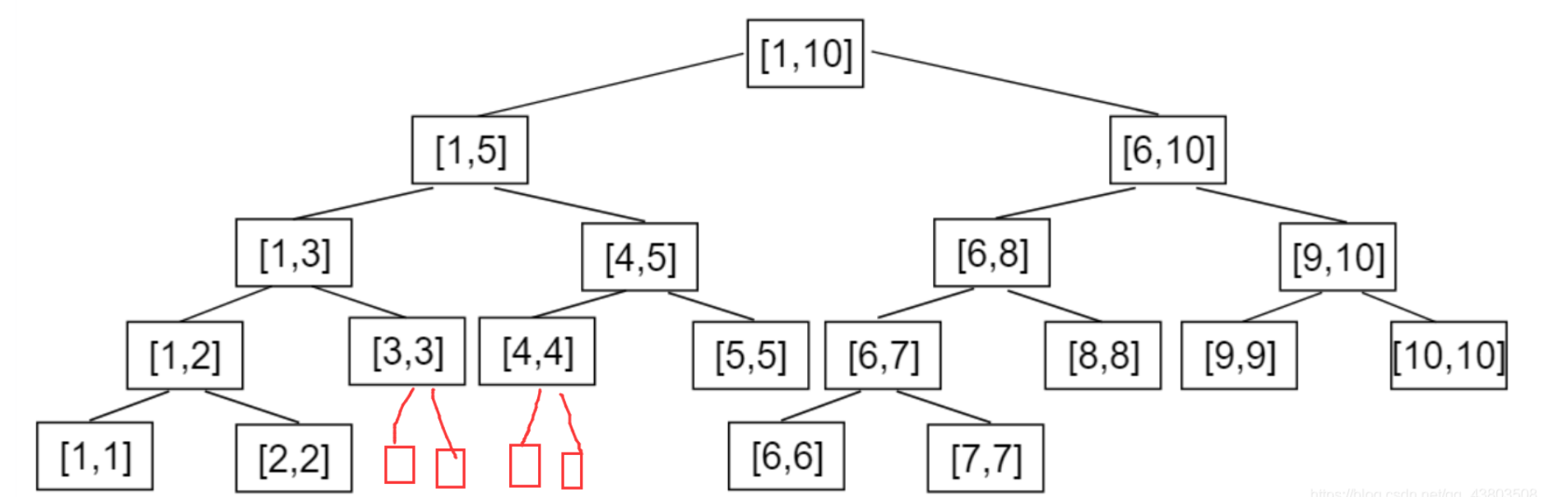
现在我们建一棵最大值为n的树,那么线段树的数组到底要开多大呢?
注意到线段树的叶子节点数量对应最大值,都是n,也就是说已知一棵二叉树(不含度为1的节点)的叶子节点数是n,那么求一个树的总节点数的通式F,保证F尽可能接近于树的总节点数且不小于总节点数。由节点度的关系有:(F-n)x3-1+n = (F-1)*2,所以有F=2n-1。
那是开2倍就够了吗?非也!
![]()
如图所示,是n=10的情况,总节点数19,但是这个19不是连续的,所以我们最保险的情况是开到最下面一层都是满的情况,倒数第二层一定不大于n,所以最后一层不大于2n,总节点数不大于4n,所以开到4n一定没问题~
-
-
例题:
-
(POJ3468)区间加&区间和。
void pushdown(int k) {
if (tree[k].lz) { // 这里因为0的话就是不变,所以不用变成inf
tree[lc].lz += tree[k].lz;
tree[rc].lz += tree[k].lz;
tree[lc].ans += (tree[lc].r - tree[lc].l + 1) * tree[k].lz;
tree[rc].ans += (tree[rc].r - tree[rc].l + 1) * tree[k].lz;
tree[k].lz = 0;
}
}
void update(int k, int l, int r, ll num) { // 当前在k节点 [l, r]区间 +num
if (tree[k].l >= l && tree[k].r <= r) {
tree[k].lz += num;
tree[k].ans += num * (tree[k].r - tree[k].l + 1);
return;
}
pushdown(k);
int mid = (tree[k].l + tree[k].r) / 2;
if (l <= mid) {
update(lc, l, r, num);
}
if (r > mid) {
update(rc, l, r, num);
}
tree[k].ans = tree[lc].ans + tree[rc].ans;
}
ll query(int k, int l, int r) {
if (tree[k].l >= l && tree[k].r <= r) {
return tree[k].ans;
}
pushdown(x);
int mid = (tree[k].l + tree[k].r) / 2;
ll ans = 0;
if (l <= mid) {
ans += query(lc, l, r);
}
if (r > mid) {
-