树状数组

1. 参考：

   1. 第一位大佬的链接：https://zhuanlan.zhihu.com/p/93795692，奶奶喂饭级别教程，强烈推荐！

   2. 算法训练营，树状数组篇

2. 简介：

   1. 名称：树状数组（Binary Index Tree，即BIT）

   2. 支持的基本操作：

      1. 单点修改，更改某个元素的值，复杂度O(logn)

      2. 区间查询，比如求区间元素和，复杂度O(logn)

      普通的数组中这两个的操作分别是O(1)和O(n)，尽管有前缀和这种操作，可是单点修改之后就需要重新计算，于是改一次查一次，复杂度爆炸，直接gg，但是这里的“破绽”在于单点修改影响了1个节点，区间修改影响了n个节点，我们想要一种数据结构，让两个的影响大致均衡，以达到降低最劣复杂度的效果，树状数组让这两个的影响“节点”均为logn。

   3. 一些abstract：

      最牛且亲民的一种数据结构，功能强大且常数较小。

3. 一些操作：

   树状数组巧妙利用了二进制，比如11(1)这个数字，我们要求第一项加到第十一项的和，于是树状数组说我可以算(0, 8]，(8, 10]，(10, 11]。注意到8=(1000)2，10=(1010)2，11=(1011)2，其实就是从左到右每次“吞掉”最左边的1（反过来看就是每次放弃最右边的1），又因为最劣的情况是都是1，这样次数最多，也不会超过logn次计算，也就是说我们只需要维护具有以上特征的区间即可，即区间左边的二进制的1，右边一定有，右边在左边二进制最后一个为1的位之后，还可以将其中一个0改成1。

   而一个值的改变会影响哪些区间呢？比如有一个数叫(100110)2，包含它的最小区间为((100100)2, (100110)2]，然后右边界要扩张，左边界要抹掉右边界的最后一个1，即大一点的区间变成((100000)2, (101000)2]，然后右边界再大一点就是(110000)2，再大一点的区间就是((100000)2, (110000)2]，再大一点呢？((0000000)2, (1000000)2]，以此类推，知道右边界比最大的n还要大，就没有修改的必要了，显然这样也不会超过logn次。

   至于如何算一个数字的最右侧的1在哪，有一个神奇的公式叫lowbit，我们规定lowbit(x) = x&(-x)。为什么成立呢？想象一下，一个数字的组成是：(abcd10000)2，则-x为(!a!b!c!d01111+1)2=(!a!b!c!d10000)2，所以二者取与，前面显然都是0，所以就把最后一个1取出来咯～

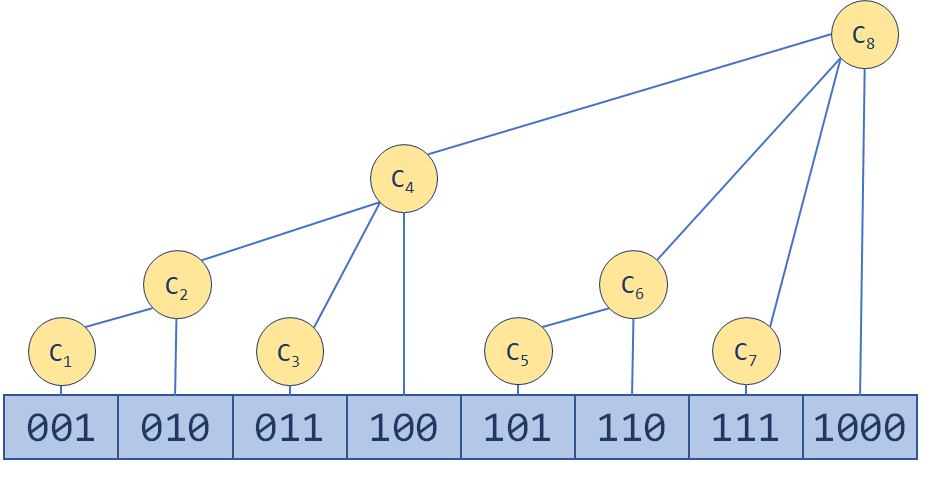
   然后最开始的数组[1, n]，虽然树状数组对应的也是[1, n]，但是每个节点，代表刚才提到的那种区间，感觉抽象就看这个图：

   

    

   可以看到树状数组和原来的数组的节点个数是一一对应的。

   1. 单点修改：

       int tree[MAXN];
       inline void update(int i, int x)  // 把i的位置的值增加x
       {
           for (int pos = i; pos < MAXN; pos += lowbit(pos))  // 比如最开始是100110；每次进一个位，下一次就是101000，然后是110000，然后是1000000...每次都代表区间的右界
               tree[pos] += x;
       }

   2. 区间查询：

       inline int query(int n)  // 查询单点前缀和
       {
           int ans = 0;
           for (int pos = n; pos; pos -= lowbit(pos))  // pos代表刚才提到的区间的右端点，每次退还最右边的1 直到
               ans += tree[pos];
           return ans;
       }
       ​
       inline int query(int a, int b)  // 查询区间和
       {
           return query(b) - query(a - 1);
       }

   活学活用（基础板子）：

    #include <cstdio>
    #include <cstring>
    #define MAXN 50005
    #define lowbit(x) ((x) & (-x))
    int tree[MAXN];
    inline void update(int i, int x)
    {
        for (int pos = i; pos < MAXN; pos += lowbit(pos))
            tree[pos] += x;
    }
    inline int query(int n)
    {
        int ans = 0;
        for (int pos = n; pos; pos -= lowbit(pos))
            ans += tree[pos];
        return ans;
    }
    inline int query(int a, int b)
    {
        return query(b) - query(a - 1);
    }
    int main()
    {
        int cases;
        scanf("%d", &cases);
        for (int I = 1; I <= cases; ++I)
       {
            memset(tree, 0, sizeof(tree));
            int n, x, a, b;
            char opr[10];
            printf("Case %d:\n", I);
            scanf("%d", &n);
            for (int i = 1; i <= n; ++i)
           {
                scanf("%d", &x);
                update(i, x);  // 数组初始化
           }
            while (scanf("%s", opr), opr[0] != 'E')
           {
                switch (opr[0])
               {
                  case 'A':
                      scanf("%d%d", &a, &b);
                      update(a, b);  // 加法，所以是正的
                      break;
                  case 'S':
                      scanf("%d%d", &a, &b);
                      update(a, -b);  // 减法，所以是负的
                      break;
                  case 'Q':
                      scanf("%d%d", &a, &b);
                      printf("%d\n", query(a, b));  // 查询[a, b]
               }
           }
       }
        return 0;
    }

4. 经典例题：

   1. 逆序对个数：

      比如现在给了一堆数字，其实你根本不关心这些数的具体值，有用的只是这些数字到底都是第几大的，然后根据这个rank来判断逆序对的个数。比如现在分别是第3、2、4、5、1大的数字，我们先构造一个全为0的数组，代表位置为i的数字有没有出现，然后遍历这个rank数组，每次遇到rank为i的数，就在新数组中查找1到i的和是多少，即已经出现了多少个比我小的数字，然后把位置为i的值变为1，代表位置为i的数字已经出现了。

      搬用大佬1的代码：

       #include <cstdio>
       #include <cctype>
       #include <algorithm>
       #define lowbit(x) ((x) & (-x))
       #define MAXN 500010
       using namespace std;
       typedef long long ll;
       ​
       ll read()  //快速读入，不是这篇文章的重点
       {
           ll ans = 0;
           char c = getchar();
           while (!isdigit(c))
               c = getchar();
           while (isdigit(c))
          {
               ans = ans * 10 + c - '0';
               c = getchar();
          }
           return ans;
       }
       ll tree[MAXN];
       inline void update(ll i, ll x)
       {
           for (ll pos = i; pos < MAXN; pos += lowbit(pos))
               tree[pos] += x;
       }
       inline ll query(int n)
       {
           ll ans = 0;
           for (ll pos = n; pos; pos -= lowbit(pos))
               ans += tree[pos];
           return ans;
       }
       inline ll query(ll x, ll y)
       {
           return query(y) - query(x - 1);
       }
       int A[MAXN]; //离散化后的数组
       typedef struct
       {
           ll value, id;
       } mypair;
       mypair B[MAXN]; //原始数组（同时存储id）
       bool cmp(mypair x, mypair y)
       {
           if (x.value < y.value)
               return true;
           else if (x.value == y.value && x.id < y.id)
               return true;
           return false;
       }
       int main()
       {
           ll n = read(), sum = 0;
           for (int i = 1; i <= n; i++)
          {
               B[i].value = read();
               B[i].id = i;  // id代表第几个位置
          }
           sort(B + 1, B + n + 1, cmp);  // 根据值排序之后，现在的B的id保留了原来的位置，即B[1].id代表第一大的值原来的位置
           for (int i = 1; i <= n; i++)
               A[B[i].id] = i;  // A[i]代表原来i的位置是第几大的
         // 核心代码
           for (int i = 1; i <= n; i++)
          {
               sum += query(A[i]);  // 遍历每个数字，因为知道是第A[i]大的，所以看看A[i]大之前的数字出现过了多少个，就新增多少个逆序对
               update(A[i], 1);  // A[i]大的数字也出现过了，更新为1
          }
           sum = n * (n - 1) / 2 - sum;
           printf("%lld\n", sum);
           return 0;
       }

   2. POJ2352，数星星。给定N（15000）个点坐标(X, Y) （X, Y范围为[0, 32000]）。我们规定一个星星的等级是有多少颗星星的横纵坐标都不大于这个点。求所有等级的星星都有多少颗。（题目要求没有星星重合的情况，但是有也能做，去个重，标记一下出现了多少次，最后算出一个点的答案，把一次变成重复次数就行了）

      显然最后的答案和星星给出的顺序无关，所以可以随便排序，不用像上一个题一样标记id，这里按照Y轴排序其次是X轴，然后每次统计一个点的时候，就看X比它小的值出现了多少个，显然在后面的都是不能算在等级范围内的，所以必然只算前面的就行，并且只需要看前面点的X轴坐标，有多少个不大于现在的x值的，就是一个区间查询，别忘了最后赋值。

   3. 给一个多叉树，树的每一个位置初始状态都有一个苹果，接下来若干次操作，C操作即如果这个地方有苹果，则摘掉，不然长出一个苹果，Q操作则查询这个位置的子树有多少个苹果。
      看起来好像没有区间查询，反倒是子树查询？有一种naive的想法是：只需要修改这个点到根的路径上所有节点的答案。但如果退化成一条链，复杂度就炸了。但又没办法变平衡，会改变父子关系。那该怎么办呢？我们需要好好分析一下这两个操作：
      　　1. C操作相当于单点修改。
      　　2. Q操作相当于区间查询，但是区间在哪，区间代表的是整个子树的区间，等下，这不就是提前跑出dfs序，保留每个节点的起止位置，然后Q操作就变为查询这个区间的和吗。
      所以就是跑出dfs序，用树状数组操作一下就ok了。

5. 扩展：多维树状数组

   谁说只能是一维的～

   一维树状数组修改和查询的时间复杂度为O(logn)，而m维树状数组时间复杂度都是O(log^mn)。数组就是m维数组啦，每一个维度的值，都和一维中的意义相同。现在以二维树状数组为例：

   操作修改如下：

   1. 前缀和：要不要举一反三一下？其实这个二维的区域面积和，固定x的那一个维度，这次计算它的宽度是相同的，然后第二维度，每次执行和一维一样的操作，只不过从区间，变成了宽一定的矩形区域。

       int query(int x, int y) {
         int s = 0;
         for (int i = x; i; i -= lowbit(i)) {
           for (int j = y; j; j -= lowbit(j)) {
             s += c[i][j];
          }
        }
         return s;
       }

   2. 更新：更新了a[x][y]，影响到的值同样也是单个维度受影响的区间的集合之“积”。

       // size假设为n x m
       void update(int x, int y, int v) {  // a[x][y] += v
         for (int i = x; i <= n; i += lowbit(i)) {
           for (int j = y; j <= n; j += lowbit(j)) {
             c[i][j] += v;
          }
        }
       }

   3. 矩形区域和：显然和普通的二维前缀和操作大同小异：

       int query(int x1, int y1, int x2, int y2) {  // 从左上角(x1, y1)到(x2, y2)的区域和
       　　return query(x2, y2) - query(x2, y1 - 1) - query(x1 - 1, y2) + query(x1 - 1, y1 - 1);
       }

6. 树状数组局限性：

   1. 不擅长区间修改，如果慢慢单点修改，复杂度将会是O(nlogn)的。

   2. 能解决“减法”的问题，比如区间的和，可以变成前缀和的减法，而像区间的最大值，就不能用前缀的减法来解决，需要用线段树才可以。

7. 待续