牛顿迭代法求平方根

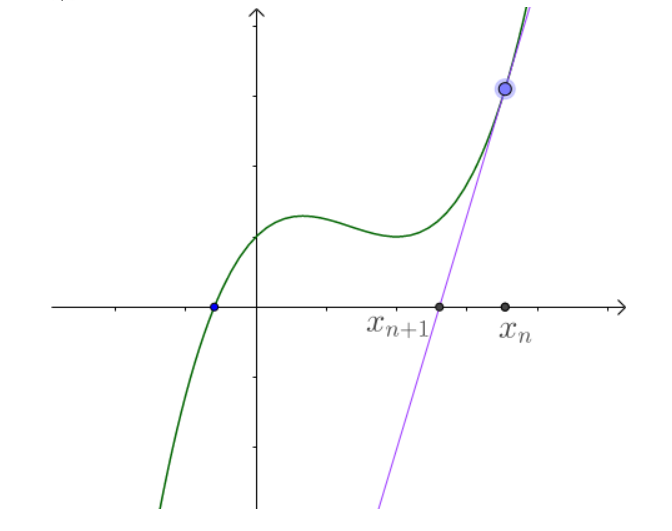
如图，一个曲线方程 \(f(x)\)，在它的 \(f(x_n)\) 处画一条切线与 \(x\) 轴相交，交点为 \(x_{n+1}\)，如果继续在它的 \(f(x_{n+1})\) 处画一条切线与 \(x\) 轴相交，会得到交点 \(x_{n+2}\)。然后重复这个过程，可以发现交点 \(x_{n+m}\) 会无限逼近方程 \(f(x)=0\) 的解，最终可以得到一个与理想值无限靠近的解。

关于为什么可以用这个方法，或者说，可以用这个方法的函数有什么条件，可以参考维基百科：

而我们这里讨论的是求平方根，很显然可以使用这个方法。比如，我们要求 N 的平方根。可以分为一下几个步骤：

• 将问题转化为求方程 \(f(x) = x^2 - N\)，当 \(f(x) = 0\) 时方程的解。
• 函数 \(f(x)\) 的导函数是：\(f^{'}(x)=2x\)
• 那么 \(f(x)\) 函数的曲线在 \((x_n,x_n^{\ 2}-N)\) 点处切线的斜率为：\(2x_n\)
• 那么切线函数为：\(g(x) = 2x_n(x-x_n) + (x_n^{\ 2} - N)\)，即：\(g(x) = 2x_nx - x_n^{\ 2} - N\)
• 所以切线与 \(x\) 轴的交点 \(x_{n+1} = \displaystyle\frac{x_n + \frac{N}{x_n}}{2}\)
• 最后，我们将得到的交点值的平方与 \(N\) 比较，循环以上过程直至得到满意的值。

对于 \(x_1\) 的值，我们选择 \(N\) 就好。

C 代码：

double abs(double x)
{
    return x < 0 ? -x : x;
}

/**
 * 精度为 0.00001
 * @param x
 * @return
 */
double sqrt(double x)
{
    if (x < 0)
        return 0;
    else
    {
        double err = 0.00001; // 设置误差范围，当误差小于这个值时我们认为得到了准确值
        double root = x;
        while (abs(x - root * root) > err)
            root = (root + x / root) / 2; // 运用牛顿迭代法的公式进行计算
        return root;
    }
}

参考：https://blog.csdn.net/chenrenxiang/article/details/78286599