结对项目
| 这个作业属于哪个课程 | https://edu.cnblogs.com/campus/gdgy/Class34Grade23ComputerScience |
|---|---|
| 这个作业要求在哪里 | https://edu.cnblogs.com/campus/gdgy/Class34Grade23ComputerScience/homework/13479 |
| 这个作业的目标 | 使用python完成小学四则运算程序,掌握结对编程的流程 |
| GitHub链接 | https://github.com/fanfanlilili/calculation |
一、成员
3123004282 韦立凡
3123004532 廖杰
二、PSP表格
| PSP2.1阶段 | Personal Software Process Stages (个人软件过程阶段) | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 20 | 30 |
| Estimate | 估计这个任务需要多少开发时间 | 5 | 5 |
| Development | 开发 | 30 | 30 |
| Analysis | 需求分析(包括学习新技术) | 60 | 60 |
| Design Spec | 生成设计文档 | 10 | 20 |
| Design Review | 设计复审 | 20 | 10 |
| Coding Standard | 代码规范(为目前的开发制定合适的规范) | 20 | 10 |
| Design | 具体设计 | 60 | 90 |
| Coding | 具体编码 | 300 | 360 |
| Code Review | 代码复审 | 20 | 20 |
| Test | 测试(自我测试,修改代码,提交代码) | 30 | 60 |
| Reporting | 报告 | 30 | 20 |
| Test Repor | 测试报告 | 20 | 30 |
| Size Measurement | 计算工作量 | 10 | 10 |
| Postmortem & Process Improvement Plan | 事后总结 | 10 | 10 |
| 合计 | 645 | 765 |
三、效能分析(耗费1.5小时)
通过在pycharm中安装line_profiler工具来进行性能分析,根据运行的结果,代码总运行时间是0.02s,整体性能不错,没有严重影响性能的瓶颈
主要瓶颈
1.耗时最大:generate_expression_ast函数耗时占总时间的一半,其中82行的generate_number的调用占约54%,95和96行的evaluate_ast各占约11%
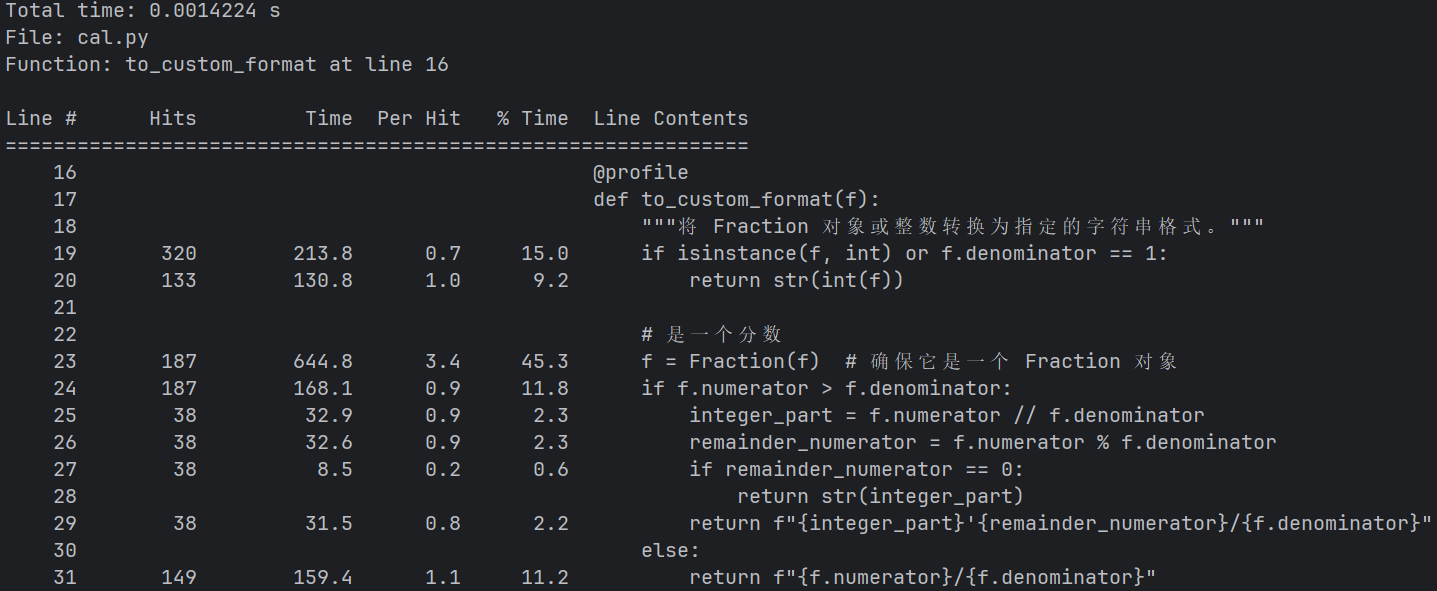
改进思路:通过缓存以生成的数字,避免重复生成
_number_cache = {}
def get_cached_number(max_range):
key = max_range
if key not in _number_cache:
_number_cache[key] = generate_number(max_range)
return _number_cache[key]
2.to_custom_format函数中第23行f = Fraction(f)调用冗余
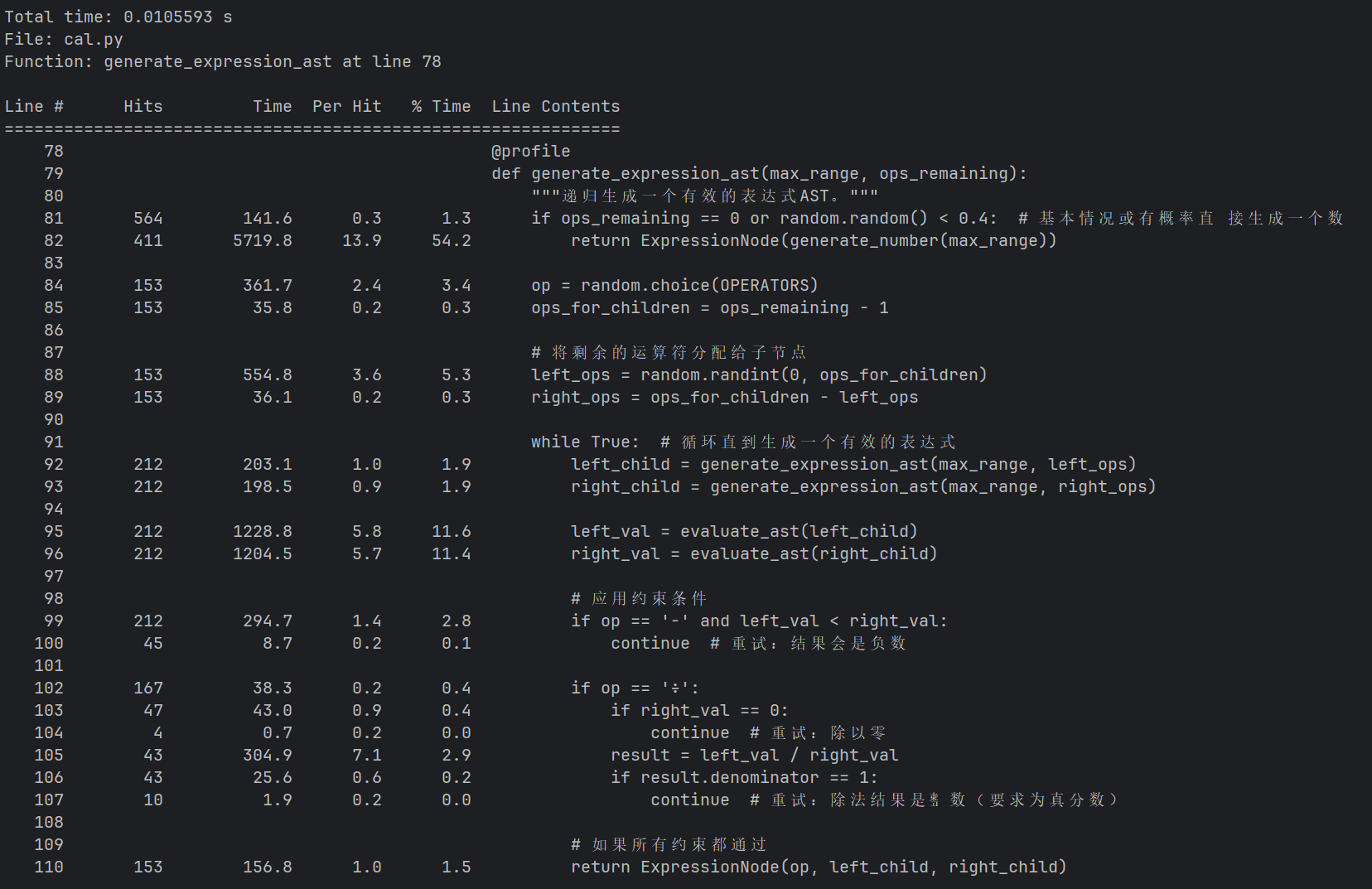
改进思路:删除冗余的fraction转换即可
def to_custom_format(f):
"""将 Fraction 对象或整数转换为指定的字符串格式。"""
if isinstance(f, int) or f.denominator == 1:
return str(int(f))
if f.numerator > f.denominator:
integer_part = f.numerator // f.denominator
remainder_numerator = f.numerator % f.denominator
if remainder_numerator == 0:
return str(integer_part)
return f"{integer_part}'{remainder_numerator}/{f.denominator}"
else:
return f"{f.numerator}/{f.denominator}"
改进结果
1.to_custom_format 函数性能提升明显(约40%)
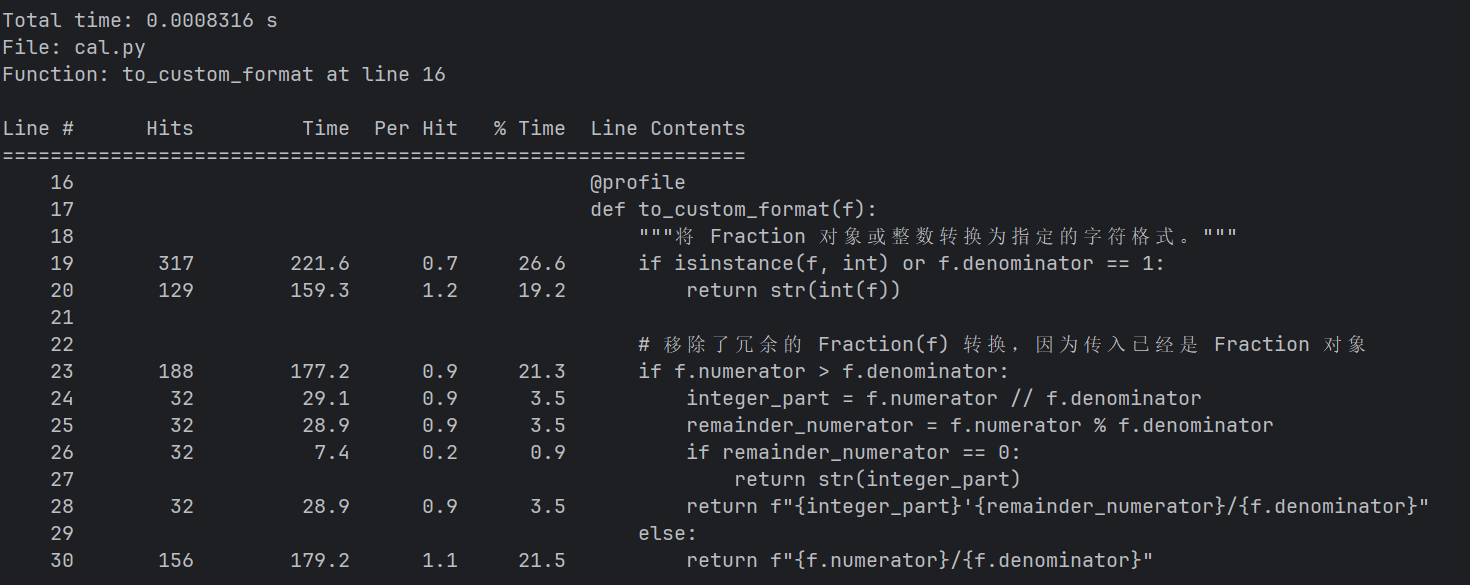
2.generate_expression_ast 函数性能则提升约10%,得益于循环次数的减少(从212次减少到160次)
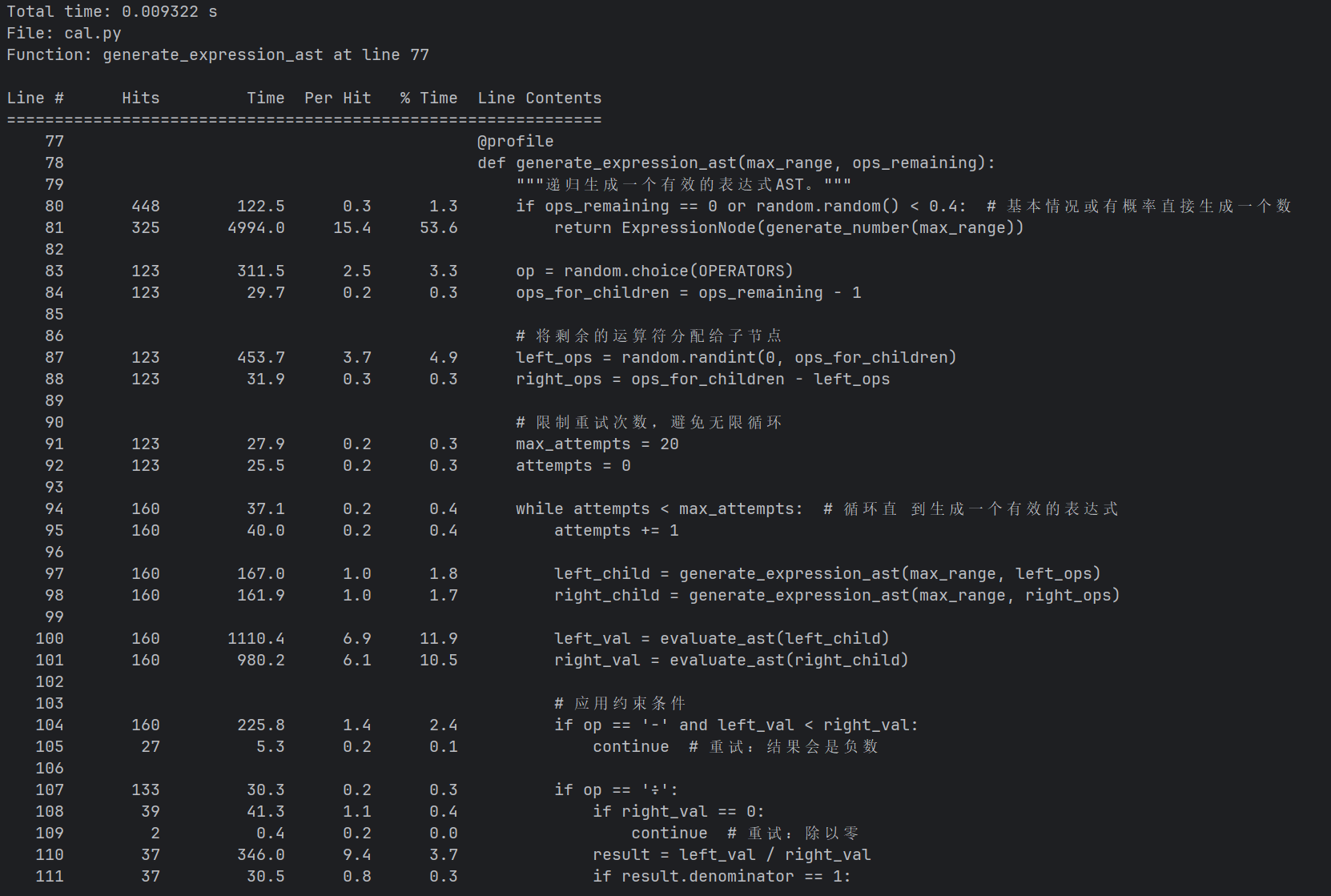
总体性能提升约7%,不过generate_expression_ast函数仍然是最大瓶颈,时间主要花在递归调用和表达式验证
四、设计实现过程
为了满足项目需求(生成题目、避免负数、保证除法为分数、去重等),我们采用了一种基于抽象语法树(Abstract Syntax Tree, AST)的核心设计思想。这种方法比直接拼接字符串更为强大和灵活,能够轻松地处理运算优先级、格式化输出和题目查重等复杂问题
1.代码组织结构
整个项目被组织在一个单独的 Python 文件 main.py 中,其内部结构按功能分为几个明确的部分:
一个核心类
ExpressionNode:这是我们数据结构的核心,用于构建表达式的抽象语法树。每个节点代表一个数字(叶节点)或一个运算符(内部节点)。内部节点有两个子节点(left 和 right),分别代表左操作数和右操作数。
一组功能函数
这些函数围绕 ExpressionNode 类工作,可以分为以下几类:
(1)数据格式化模块 (2个函数):
to_custom_format(): 将内部表示的 Fraction 对象(分数)转换为题目要求的字符串格式(如 2'1/3)。
from_custom_format(): 将字符串格式的数字解析回 Fraction 对象,用于答案批改。
(2)表达式生成模块 (3个函数):
generate_number(): 一个辅助函数,用于生成符合范围 r 的随机自然数或真分数。
generate_expression_ast(): 核心生成函数。它通过递归方式构建一个随机的AST。这是所有题目约束(如无负数、除法为分数)被强制执行的地方。
generate_problems(): 顶层控制函数,调用 generate_expression_ast() 来生成指定数量 -n 的题目,并通过 get_canonical_form() 来确保题目不重复。
(3)AST处理模块 (3个函数):
evaluate_ast(): 递归遍历AST,计算出表达式的精确答案。
format_ast_to_string(): 递归遍历AST,将其转换为符合人类阅读习惯的字符串,并根据运算符优先级自动处理括号。
get_canonical_form(): 去重关键函数。它为每个AST生成一个唯一的“范式”,通过对可交换运算符(+, ×)的操作数进行排序,确保 2 + 3 和 3 + 2 具有相同的范式。
(4)应用主逻辑模块 (2个函数):
check_answers(): 实现 -e 和 -a 参数的功能,读取文件并进行答案批改。
main(): 程序的入口点,负责解析命令行参数,并根据参数决定是调用 generate_problems() 还是 check_answers()。
2.关键函数工作流程
本节将详细描述两个核心函数 generate_expression_ast 和 check_answers 的工作流程。
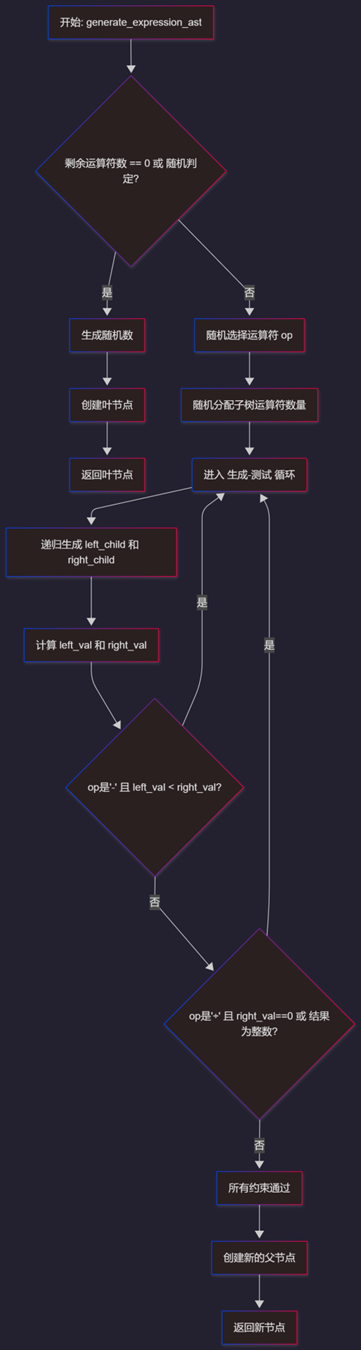
generate_expression_ast() 工作流程
此函数是整个程序逻辑最复杂的函数,其工作流程如下:
(1)递归基准条件
检查剩余待生成的运算符数量。如果为0,或随机判定,则直接生成一个数字节点(ExpressionNode)并返回,终止当前分支的递归。
(2)递归主体
①随机选择一个运算符(+, -, ×, ÷)。
②将剩余的运算符数量随机分配给左、右两个子树。
③进入一个无限循环 (while True),以确保生成的子表达式满足所有约束条件:
④递归调用 generate_expression_ast() 来生成左、右子节点。
⑤调用 evaluate_ast() 计算出左右子表达式的数值。
⑥执行约束检查:如果运算符是 -,检查是否 左数值 < 右数值。如果是,则放弃本次生成的子树,继续循环以重新生成;如果运算符是 ÷,检查是否 右数值 == 0(避免除零)或 左数值 / 右数值 的结果为整数。如果是,则放弃并继续循环。
⑦成功退出: 如果所有约束检查都通过,则用当前运算符和生成的左右子节点创建一个新的 ExpressionNode,跳出循环并将其返回。
这个流程确保了任何最终生成的表达式树都是完全符合题目要求的。
(3)check_answers() 工作流程
此函数负责执行判卷任务,其逻辑是一个线性的、按部就班的处理流程:
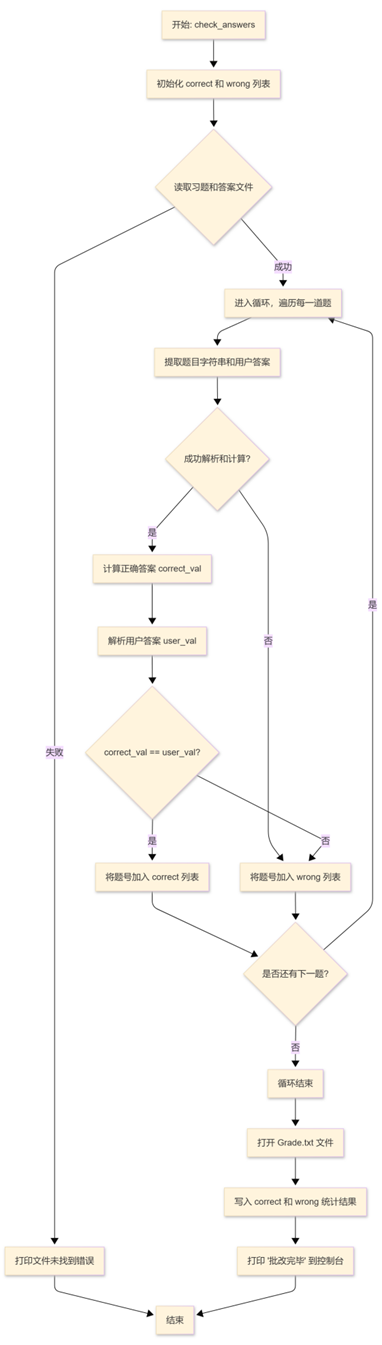
①初始化:
创建两个空列表:correct_indices 用于存放正确题目的编号,wrong_indices 用于存放错误题目的编号。
②文件读取:
尝试读取 -e 参数指定的习题文件和 -a 参数指定的答案文件的所有行。
如果任何一个文件未找到,则捕获异常,打印错误信息并终止函数。
③逐行批改:
进入一个循环,遍历读取到的每一道习题。
在循环内部,对每一行(即每一道题)执行以下操作:
a. 数据提取: 从习题行中解析出题目表达式字符串,并从对应的答案行中解析出用户作答的答案字符串。
b. 计算正确答案: 调用一个安全的求值函数 (safe_eval_wrapper),将题目表达式字符串计算出其精确的 Fraction 结果。
c. 解析用户答案: 调用 from_custom_format() 函数,将用户作答的字符串(例如 3'1/4)也转换为 Fraction 对象。
d. 比较与记录: 比较计算出的正确答案和用户答案。
- 如果两者相等,则将当前题号添加到 correct_indices 列表。
- 如果不相等,或在处理该行的任何步骤中发生错误,则将当前题号添加到 wrong_indices 列表。
④生成报告:
循环结束后,打开 Grade.txt 文件进行写入。
根据 correct_indices 和 wrong_indices 两个列表的内容,格式化并写入最终的统计结果(例如 Correct: 5 (1, 3, 5, 7, 9))。
五、代码说明
以下是项目中几个最关键的代码片段及其设计思路。
1.表达式生成与约束检查
这是在 generate_expression_ast 函数中实现的,while True 循环是确保所有约束都被满足的关键。
这是在 generate_expression_ast 函数中实现的,while True 循环是确保所有约束都被满足的关键。
def generate_expression_ast(max_range, ops_remaining):
op = random.choice(OPERATORS)
# ... 分配子节点运算符数量 ...
while True: # 循环直到生成一个有效的表达式
left_child = generate_expression_ast(max_range, left_ops)
right_child = generate_expression_ast(max_range, right_ops)
# 计算出子表达式的值,用于检查约束
left_val = evaluate_ast(left_child)
right_val = evaluate_ast(right_child)
# 约束1:减法结果不能为负数
if op == '-' and left_val < right_val:
continue # 不满足条件,重新生成左右子树
# 约束 2:除法不能除以0,且结果必须是真分数
if op == '÷':
if right_val == 0:
continue # 避免除零
result = left_val / right_val
if result.denominator == 1:
continue # 结果是整数,不符合要求,重新生成
# 如果所有约束都通过,则创建节点并跳出循环
return ExpressionNode(op, left_child, right_child)
思路与注释
递归构建: 通过递归调用,程序可以构建出任意深度的表达式树(本项目限制在3个运算符内)。
生成后验证 (Generate-and-Test): 我们采用“先生成,再验证”的模式。while True 循环确保了只有通过所有约束检查的表达式片段才能被接受。这种方式虽然可能有性能开销(少数情况下会多次重试),但逻辑清晰,易于实现和扩展新的约束。
2.通过“范式”实现题目去重
get_canonical_form 函数是去重的核心。它将一个表达式AST转换成一个唯一的、可哈希的元组(Tuple)。
def get_canonical_form(node):
"""创建一个唯一的、排序过的AST表示,用于检测重复题目。"""
if node.is_leaf():
# 叶节点(数字)的范式就是其分子分母元组
return (node.value.numerator, node.value.denominator)
op = node.value
left_canonical = get_canonical_form(node.left)
right_canonical = get_canonical_form(node.right)
# 核心逻辑:对于可交换运算符,对子节点的范式进行排序
if op in ['+', '×']:
# 使用 key=str 确保不同类型(元组和字符串)之间可以稳定排序
return (op, tuple(sorted((left_canonical, right_canonical), key=str)))
else: # 对于-和÷,顺序是固定的
return (op, left_canonical, right_canonical)
六、测试运行
我们设计了12个测试用例,覆盖了所有项目需求,以确保程序的正确性。
| # | 测试目的 | 命令 | 预期结果 | 如何确认正确性 |
|---|---|---|---|---|
| 1 | 基本生成功能 | python main.py -n 10 -r 10 | 成功生成 Exercises.txt 和 Answers.txt 两个文件,每个文件包含10道题目/答案,程序正常退出。 | 检查文件是否存在且内容行数正确,验证了 -n 和 -r 参数的基本功能。 |
| 2 | 负数约束 | python main.py -n 1000 -r 20 | 生成的1000道题目中,任何形如 a - b 的表达式,其计算结果都不应为负数。 | 手动抽查或编写脚本检查 Exercises.txt,确认所有减法 a - b 均满足 a >= b。验证了减法约束。 |
| 3 | 除法约束 | python main.py -n 1000 -r 20 | 生成的1000道题目中,任何形如 a ÷ b 的表达式,其计算结果都不能是整数。 | 检查 Answers.txt 中所有题目的答案,确认没有任何一道题的最终答案或中间除法步骤结果为整数(除非原始数字是整数)。验证了除法约束。 |
| 4 | 运算符数量约束 | python main.py -n 500 -r 15 | 生成的题目中,每道题的运算符(+, -, ×, ÷)数量都不超过3个。 | 抽查 Exercises.txt,目视检查确认运算符数量在1到3个之间。验证了题目复杂度约束。 |
| 5 | 加法去重 | python main.py -n 10000 -r 5 | 生成一万道题,由于数值范围很小,必然会产生大量等价题目。程序应能过滤掉重复项,最终成功生成一万道不重复的题目。 | 运行时间会较长,但最终会成功。如果 2+3 和 3+2 被视为不同,程序会很快完成;反之,则需要更多时间寻找不重复的组合。这验证了去重逻辑(特别是加法交换律)在起作用。 |
| 6 | 乘法去重 | python main.py -n 10000 -r 5 | 同上 | 与测试5同理,验证了乘法交换律的去重。 |
| 7 | 复杂结构去重 | python main.py -n 10000 -r 6 | 表达式 3 × (1 + 2) 和 (2 + 1) × 3 应被视为重复。 | 在大批量生成中,这两者不会同时出现。通过 get_canonical_form 的逻辑可以推断其正确性,因为子表达式 (1+2) 和 (2+1) 的范式相同。 |
| 8 | 文件格式正确性 | python main.py -n 5 -r 10 | Exercises.txt 和 Answers.txt 的格式应为 题号. 题目/答案,分数应以 a'b/c 或 b/c 的形式展示。 | 打开生成的文件,检查格式是否完全符合要求。验证了自定义格式化函数的正确性。 |
| 9 | 答案批改(全对) | python main.py -e Exercises.txt -a Answers.txt | 首先生成一组题目和答案。然后用生成的答案文件去批改。Grade.txt 应显示 Correct: N (1, 2, ..., N),Wrong: 0 ()。 | 验证了 check_answers 函数在答案完全正确时的逻辑。 |
| 10 | 答案批改(部分错误) | 手动修改 Answers.txt 中的几行,例如将 3/5 改为 4/5。然后运行 python main.py -e Exercises.txt -a Answers.txt。 | Grade.txt 应准确地报告被修改的题号为 Wrong,其余为 Correct。 | 验证了 check_answers 函数识别错误答案的能力。 |
| 11 | 参数错误处理 | python main.py | 程序应报错,并打印帮助信息,提示用户如何正确使用参数。 | 验证了 main 函数中的参数校验逻辑。 |
| 12 | 范围参数错误处理 | python main.py -n 10 -r 1 | 程序应报错,提示 -r 参数必须大于等于2。 | 验证了对 -r 参数的边界条件检查,因为小于2的范围无法生成真分数。 |
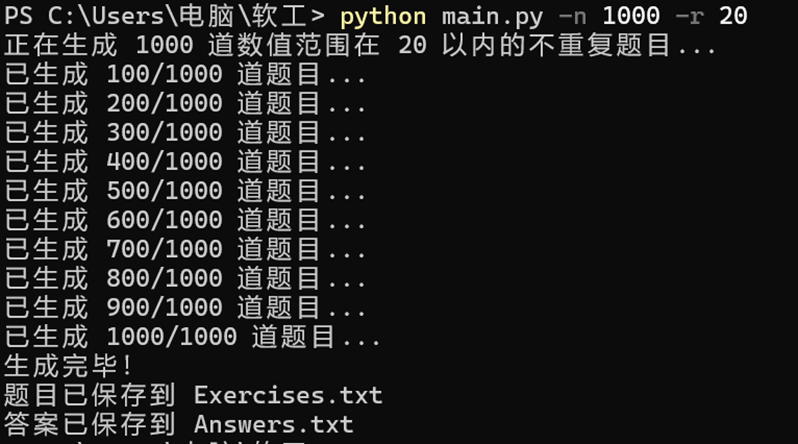
(1)基本生成功能

成功生成 Exercises.txt 和 Answers.txt 两个文件,每个文件包含10道题目/答案,程序正常退出
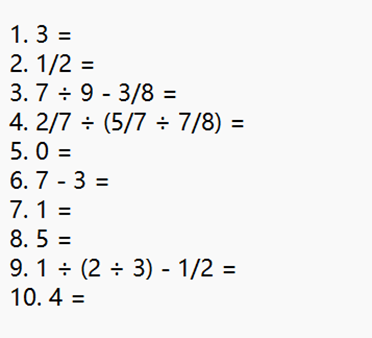

(2)负数约束
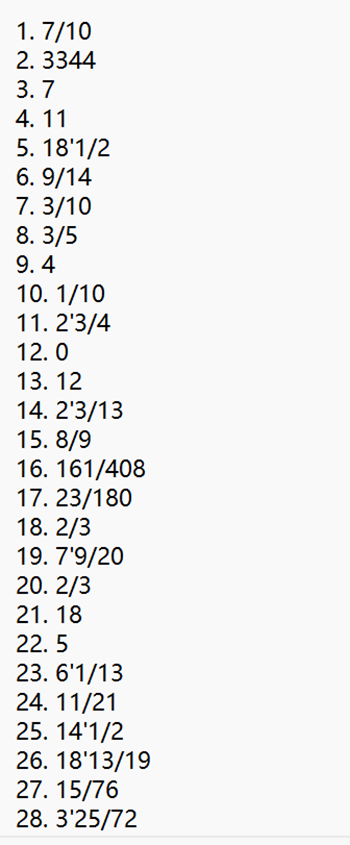
生成的1000道题目中,任何形如 a - b 的表达式,其计算结果都不应为负数。
如图截取几个例子符合约束:

(3)除法约束
生成的1000道题目中,任何形如 a ÷ b 的表达式,其计算结果都不能是整数。
如图截取几个例子 符合约束:


(4)运算符数量约束
生成的题目中,每道题的运算符(+, -, ×, ÷)数量都不超过3个。
如图随机抽取符合例子:

(5)(6)(7)成功生成一万个例子并且符合:加法去重、乘法去重、复杂结构去重
一万个例子:
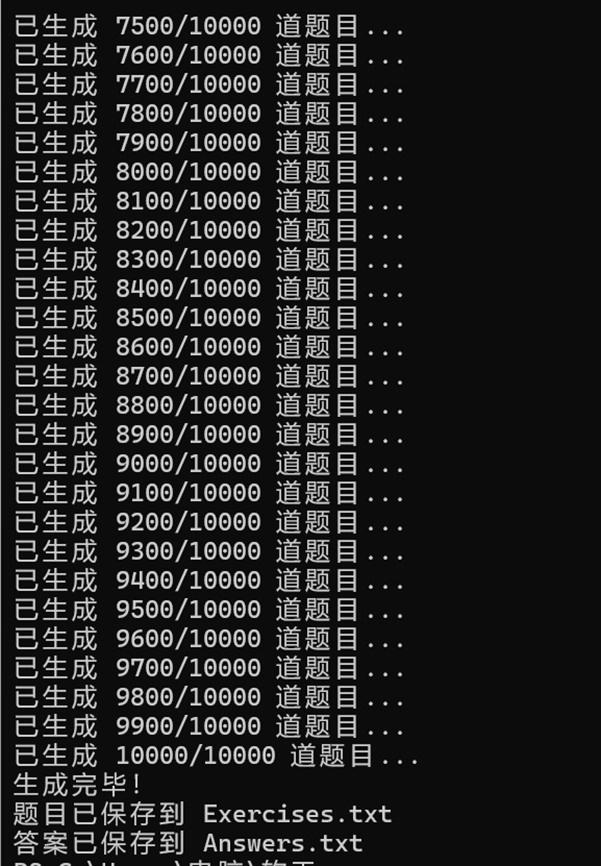


如果 2+3 和 3+2 被视为不同,程序会很快完成;反之,则需要更多时间寻找不重复的组合。这验证了去重逻辑(特别是加法交换律)在起作用。与测试5同理,验证了乘法交换律的去重。在大批量生成中,这两者不会同时出现。通过 get_canonical_form 的逻辑可以推断其正确性,因为子表达式 (1+2) 和 (2+1) 的范式相同。
均没有重复项,均符合约束。
(8)文件格式正确性
Exercises.txt 和 Answers.txt 的格式应为 题号. 题目/答案,分数应以 a'b/c 或 b/c 的形式展示。
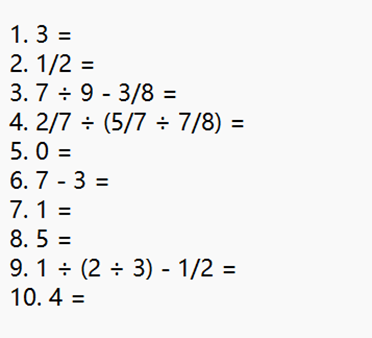

(9)答案批改(全对)
首先生成一组题目和答案。然后用生成的答案文件去批改。Grade.txt 应显示 Correct: N (1, 2, ..., N),Wrong: 0 ()。
用1的例子来做显示如下:

(10)答案批改(部分错误)
手动修改前三题的答案:1/8改为1 31改为3 8改为81


结果如下:

验证正确
(11)参数错误处理
输入python main.py程序应报错,并打印帮助信息,提示用户如何正确使用参数。

(12)范围参数错误处理
程序应报错,提示 -r 参数必须大于等于2。

七、项目小结
1.成功之处
(1)更优的设计方案:项目初期,我们在“如何表示和生成表达式”有分歧。经过讨论,我们最终放弃了简单的字符串处理,共同选择了抽象语法树(AST)作为核心数据结构。事实证明,这个决定是项目的最大亮点,它解决了处理运算优先级、添加括号、题目查重等难题。
(2)更高的代码质量:一人编码、一人审查的模式让很多低级错误(如拼写错误、逻辑疏忽)在萌芽阶段就被发现,明显提升代码健壮性
(3)知识共享与共同成长:廖杰在整体架构和算法设计上更具条理,而韦立凡在代码实现细节和调试上嗅觉敏锐。通过结对,我们互相学到了对方的优点。整个项目下来,我们都感觉自己的能力得到了补强。
(4)攻坚克难的效率:项目中最难的部分是“题目去重”。我们一起设计了“表达式范式”get_canonical_form()函数,通过对可交换运算符的子节点进行排序,完美解决了这个问题,此过程也让我们感受到了结对编程的效率。
2.教训
(1)编程角色的挑战:有时候,当编程者思维活跃时,辅助者很难插上话,容易变成一个被动的“代码检视员”。反之,当编程者卡壳时,辅助如果不能及时提供有效思路,场面会一度陷入尴尬。我们仍需学习如何动态、高效地切换角色。
(2)时间管理的冲突:两个人要找到大段的、共同的、高效的工作时间并不容易,这也提醒我们,好的结对编程需要有严格的时间规划和承诺。
3.结对感受
廖杰:韦立凡更注重代码细节,几次在我陷入僵局时,他帮助我定位到隐藏极深的 bug。他提出的 while True 循环来确保约束满足的“生成-测试”模型,虽然简单粗暴,但异常有效。和他搭档,总能感受到一种积极解决问题的能量。
韦立凡:项目初期,是廖杰坚持要使用抽象语法树,为整个项目的成功奠定了坚实的基础。我对约束条件不敏感,是他用清晰的流程图和逻辑描述将问题梳理得井井有条,他的严谨和远见为我节约了大量时间。
4.总结
总而言之,这次“四则运算生成器”的结对编程经历远超预期。从最初的需求分析到最终的代码实现,它不仅仅是两个人合作完成了一个项目,更是一次关于沟通、信任和团队协作的深度实践,让我们明白清晰的分工和灵活的角色切换是效率的保障。虽然过程会有错误和争论,但最终我们仍然做出了我们都满意的作品,它所带来的成就感是无可比拟的。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号