近期

python z3库学习

常用API

https://i.postimg.cc/zf8TgQfj/image.png
1、创建约束求解器
solver = Solver()
2、添加约束条件（这一步是z3求解的关键）
solver.add()
3、判断解是否存在
if(solver.check()==sat)
4、求解
print(solver.model())

基础使用

1. 声明

   x = Int('x')	#声明整数
   x = Real('x')	#声明实数
   x = Bool('x')	#声明布尔类型
   a, b, c = Reals('a b c')	#批量声明
   

2. 解不等式

   x = Int('x')
   y = Int('y')
   solve(x > 2, y < 10, x + 2*y == 7)
   print(solver.model())
   

   通过约束调节可以得出[y = 0, x = 7]当满足条件很多时，只会输出一组解

3. 约束条件化简

   x = Int('x')
   y = Int('y')
   print (simplify(x + y + 2*x + 3))
   print (simplify(x < y + x + 2))
   print (simplify(And(x + 1 >= 3, x**2 + x**2 + y**2 + 2 >= 5)))
   

   输出

   3 + 3*x + y Not(y <= -2) And(x >= 2, 2*x**2 + y**2 >= 3)
   

4. Z3提供了所有基本的数学运算。 Z3Py使用Python语言的相同运算符优先级。 像Python一样，**是幂运算。 Z3可以求解非线性多项式约束。

   x = Real('x')
   y = Real('y')
   solve(x**2 + y**2 > 3, x**3 + y < 5)
   

​ 输出[x = 1/8, y = 2]其中，Real('x')创建实际变量x。 Z3Py可以表示任意大的整数，有理数（如上例）和无理代数。 一个无 理数代数是具有整数系数的多项式的根。 在内部，Z3精确地代表了所有这些数字。 无理数以十进制表示形式显示，以便读取结果。

5. Z3支持布尔运算符：And, Or, Not, Implies (implication), If (if-then-else)。双蕴含符号用==表示。 以下示例显示如何解决一组简单的布尔约束。

   p = Bool('p') 
   q = Bool('q') 
   r = Bool('r') 
   solve(Implies(p, q), r == Not(q), Or(Not(p), r))
   

6. 函数

   x = Int('x') 
   y = Int('y') 
   f = Function('f', IntSort(), IntSort()) solve(f(f(x)) == x, f(x) == y, x != y)
   

   输出[x = 0, y = 1, f = [0 -> 1, 1 -> 0, else -> 1]]

ida远程调试Linux程序（转）

将IDA安装目录dbgsrv文件夹里的linux_server64拷贝到64位的linux虚拟机中；
通过命令chmod +x linux_server64为程序添加可执行权限；
通过命令./linux_server64开启服务端；
在IDA中点击Debugger，添加Remote Linux Debugger

UniverseFinalAnswer wp

解压后打开文件 找到主函数

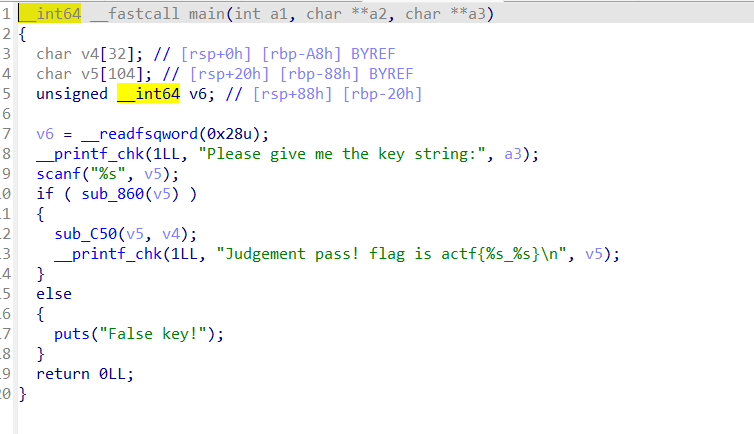
打开sub_860

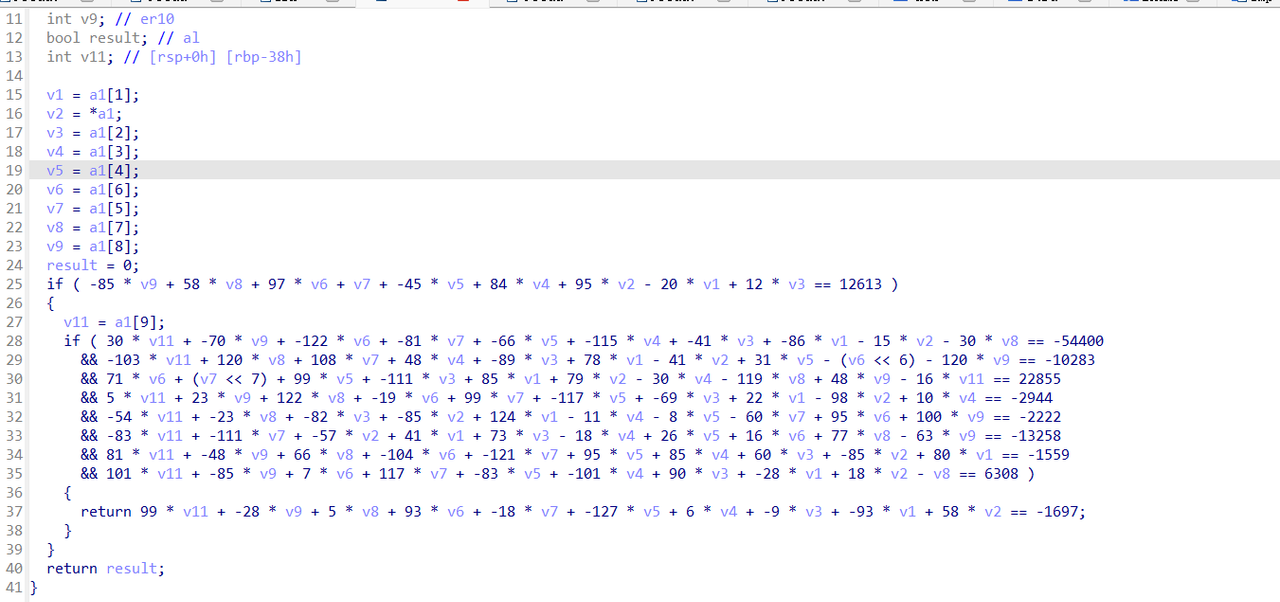
通过python z3 库写脚本

得出[v1 = 48,
v6 = 95,
v2 = 70,
v4 = 82,
v11 = 64,
v3 = 117,
v5 = 84,
v9 = 119,
v8 = 55,
v7 = 121]
同时按顺序转成字符串输出
0FuRT_y7w@
之后再注意到ida中对其有调换 v1和v2 v6和v7

所以调整后
F0uRTy_7w@
将其用虚拟机输入
完成