QOJ-8833 Equalizer Ehrmantraut

QOJ-8833 Equalizer Ehrmantraut

tag: 分类讨论，计数，构造

定义两个长度为 \(n\) 的数组 \(a\) 和 \(b\) 是 “几乎相等” (almost equal) 的，当且仅当它们满足以下条件：

• 对于任意的下标 \(1 \le i < j \le n\)，都有 \(\min\{a_i, b_j\} = \min\{a_j, b_i\}\)。

给定 \(n\) 和 \(m\)，数组中的元素必须是 \([1, m]\) 之间的整数，计算有多少对数组 \((a, b)\) 是 “几乎相等” 的。答案对 \(998244353\) 取模。

\(1 \le n, m \le 10^6\)。

设 \(\min\{a_i,b_j\}=\min\{a_j,b_i\}=x\)。分类讨论：

1. 首先 \(a=b\) 肯定是合法的，这部分贡献为 \(m^n\)。下面讨论至少有一个位置不等的情况。

2. 不妨先设某一位置满足 \(a_i<b_i\)，现在要确定任一 \(a_j,b_j\) 的合法取值方案。如下图，讨论 \(a_j<a_i,a_j=a_i,a_j>a_i\) 三种情况：

   • 若 \(a_j<a_i\)，则 \(a_j=b_j\)；
   • 若 \(a_j=a_i\)，则 \(a_j<b_j\)；
   • 若 \(a_j>a_i\)，则无解。

   

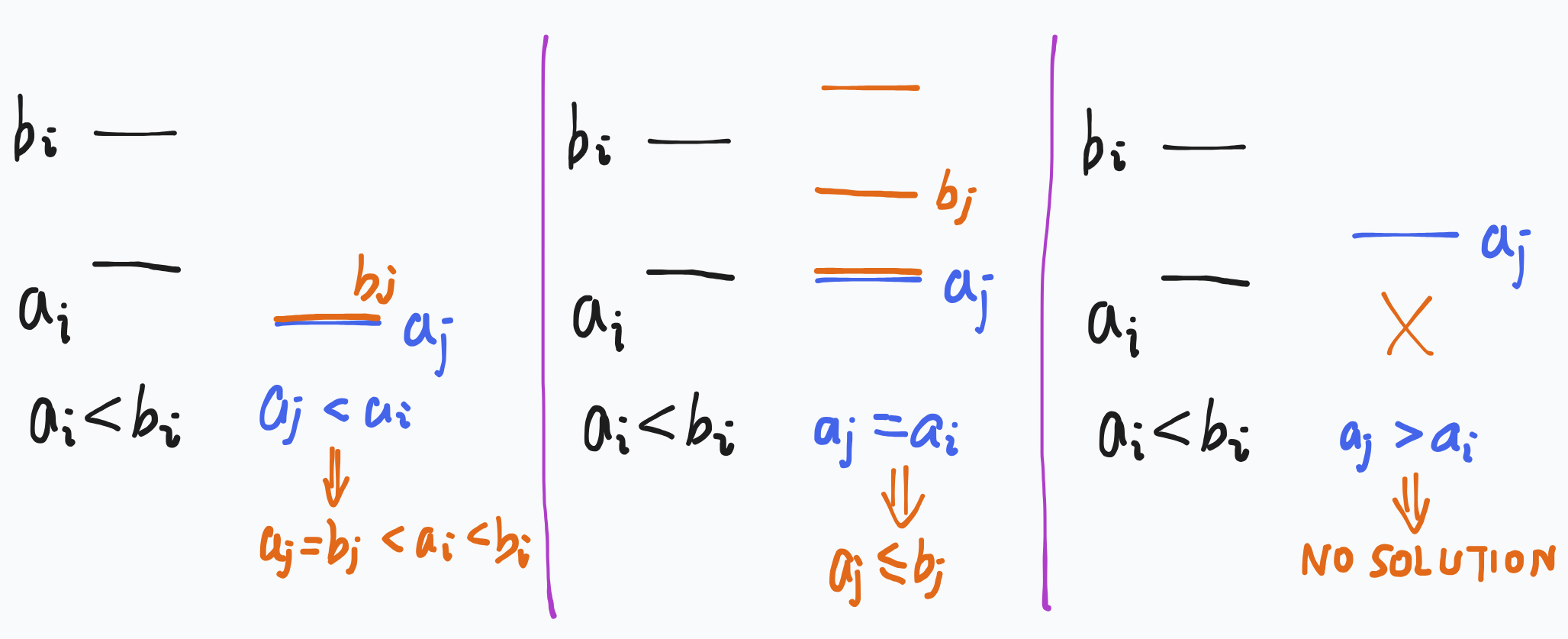
   也就是说，一旦有一个位置满足 \(a_i<b_i\)，那么其他位置都需要满足 \(a_j\le b_j\)，且：

   • \(a_j<b_j\) 的位置中 \(a_j\) 需要全相等，即为 \(x\)；
   • \(a_j=b_j\) 的位置中需要满足 \(a_j\le a_i\)。

   计数：钦定 \(x\in[1,m]\)，则 \(a_j=x<b_j\in[x+1,m]\)，或 \(a_j=b_j\le x\)，故每个位置有 \((m-x)+x=m\) 种方案，共有 \(m^n\) 种。

   注意，这种计数方式包含了情况 1，即 \(a\) 和 \(b\) 完全相等的情况，所以要减去，共有 \(x^n\) 种。接着对所有 \(x\) 求和。

3. 设某一位置满足 \(a_i>b_i\)，情况完全对称，故将情况 2 的数量乘二即可。

因此，答案为 \(m^n+2\sum_{x=1}^m(m^n-x^n)=(2m+1)m^n-2\sum_{x=1}^mx^n\)，直接用快速幂计算，时间复杂度 \(O(m\log n)\)。

Submission #1775496 - QOJ.ac