洛谷-P13736 [JOIGST 2025] 日本浮现 / Japan Emerges

洛谷-P13736 [JOIGST 2025] 日本浮现 / Japan Emerges

tag: 图论建模，Kruskal

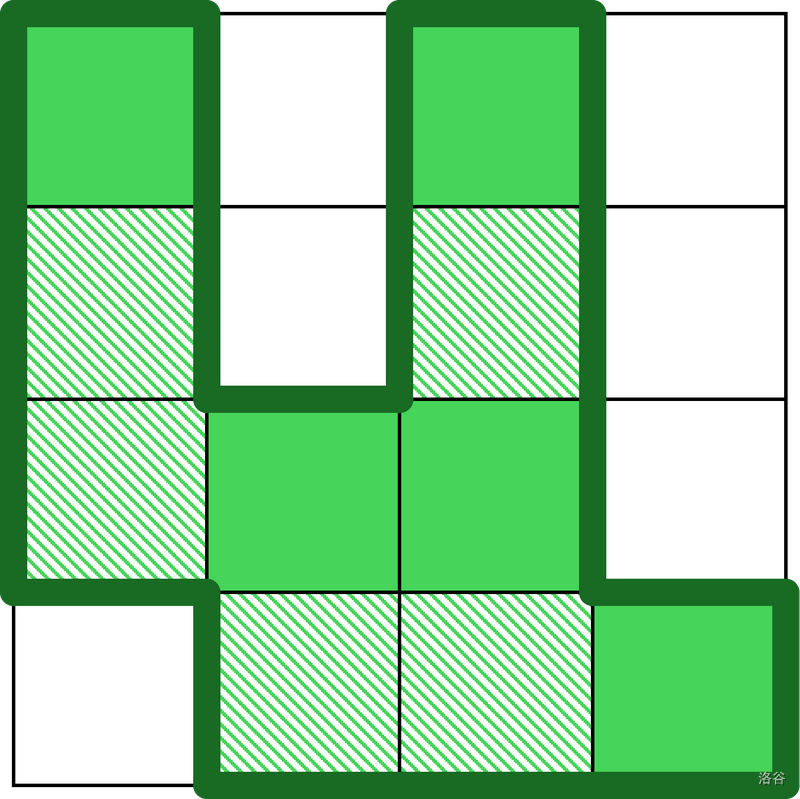
给定 \(H\times W\) 网格，开始时有 $ N $ 格是陆地，其他是海洋，每天陆地会向下蔓延一格。问最少多少天以后，所有陆地连通。如下图：

\(1\le H,E\le2\times10^5\)，\(2\le N\le\min\{HW,2\times10^5\}\)。

统计从一个陆地网格到其下面（同一列或左右两列）的第一个陆地网格所需的时间。

将每一个陆地网格视为节点，向下蔓延所需时间为边权，向蔓延到的下一个陆地网格连边。

这样就好做了，一种想法是二分答案，使用所有边权小于等于 \(x\) 的边，验证是否能连通。

另一种想法，考虑一天一天过去，可使用的边权也在增加，这与最小生成树 Kruskal 的过程类似。

因此直接跑 Kruskal，最后一个加入的边的权值即为答案。

#include <bits/stdc++.h>
#define f(i, a, b) for (int i = (a); i <= (b); ++i)
#define fi first
#define se second
#define pb push_back
using namespace std;
typedef vector<int> vi;
typedef vector<vector<int> > vvi;
typedef vector<pair<int, int> > vii;

void solve() {
    int h, w, n; cin >> h >> w >> n;
    vii p(n + 1);
    f(i, 1, n) cin >> p[i].fi >> p[i].se;
    sort(p.begin() + 1, p.end());
    vvi col(w + 1);
    f(i, 1, n) col[p[i].se].pb(i);

    struct Edge {
        int u, v, w;
        inline bool operator<(Edge const &o) const {
            return w < o.w;
        }
    };
    vector<Edge> e;
    vi ptr(w + 1, 0);
    f(i, 1, n) {
        f(j, p[i].se - 1, p[i].se + 1) {
            if (j < 1 || j > w) continue;
            while (ptr[j] < col[j].size() && p[col[j][ptr[j]]].fi < p[i].fi) {
                ++ptr[j];
            }
            if (j == p[i].se) ++ptr[j];
            if (ptr[j] >= col[j].size()) continue;
            int nxt = col[j][ptr[j]];
            e.pb((Edge){i, nxt, p[nxt].fi - p[i].fi - (p[i].se == p[nxt].se)});
        }
    }

    vi fa(n + 1);
    auto getfa = [&](auto &&self, int x) -> int {
        return x == fa[x] ? x : fa[x] = self(self, fa[x]);
    };
    iota(fa.begin() + 1, fa.end(), 1);

    int cnt = 1;
    sort(e.begin(), e.end());
    for (auto [u, v, w]: e) {
        int fu = getfa(getfa, u), fv = getfa(getfa, v);
        if (fu ^ fv) {
            fa[fu] = fv;
            ++cnt;
            if (cnt == n) {
                cout << w << '\n';
                return;
            }
        }
    }

    cout << "-1\n";

    return;
}

signed main() {
    cin.tie(0)->sync_with_stdio(false);

    int tt = 1;
    // cin >> tt;
    while (tt--) solve();

    return 0;
}