AtCoder ABC408 EF

E - Minimum OR Path（位运算，贪心）

给定 \(N\) 个节点 \(M\) 条边的无向图，其中边 \((u_i,v_i)\) 有权值 \(w_i\)。保证图连通，无自环，但不保证没有重边。

设一条路径的权值为路径上所有边的权值 按位或 的结果。求从 \(1\) 到 \(N\) 的最短路。

\(1\le N,M\le2\times10^5\)。\(0\le w_i<2^{30}\)。

首先，常规最短路的做法肯定是不对的，因为局部最小不一定是全局最小。

例如下图，设 \(d(i)\) 表示从 \(1\) 到 \(i\) 的最短或路径，那么 \(d(3)=1\)，但是 \(d(4)=4\operatorname{OR}4\operatorname{OR}4=4\)，而不是 \(d(3)\operatorname{OR}4=1\operatorname{OR}4=5\)。

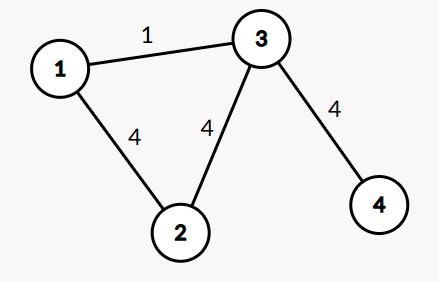
对于涉及到位运算的题，我们可以想想如何 按位考虑。

由于是求最小的或的结果，根据 贪心 的思想，我们从高位到低位依次考虑，从全为 \(1\) 开始，尽量把高位变成 \(0\)，判断能否成为答案。

每次都相当于是删掉了权值这一位上为 \(1\) 的边，然后看能否到达（也就是判断是否连通）。

这样就变成了一个 判定性问题。而判断 \(1\) 和 \(N\) 是否连通，可以用并查集。

故复杂度为 \(O((N+M)\log R)\)，其中 \(R\) 为边权的值域大小。

#include <bits/stdc++.h>
using namespace std;

signed main() {
    cin.tie(0)->sync_with_stdio(false);

    int n, m;
    cin >> n >> m;
    vector<tuple<int, int, int>> e(m);
    for (auto &[u, v, w]: e) {
        cin >> u >> v >> w;
        --u, --v;
    }
    int ans = (1 << 30) - 1;
    auto check = [&](int msk) {
        vector<int> fa(n);
        function<int(int)> getfa;
        getfa = [&](int x) {
            return x == fa[x] ? x : (fa[x] = getfa(fa[x]));
        };
        iota(fa.begin(), fa.end(), 0);
        for (auto [u, v, w]: e) {
            if ((w & msk) != w) continue;
            int fu = getfa(u), fv = getfa(v);
            if (fu ^ fv) {
                fa[fu] = fv;
            }
        }
        return getfa(0) == getfa(n - 1);
    };
    for (int i = 29; i >= 0; i--) {
        int tmp = ans ^ (1 << i);
        if (check(tmp)) ans = tmp;
    }
    cout << ans;

    return 0;
}

F - Athletic（数据结构优化 DP）

有 \(N\) 个平台，第 \(i\) 个平台的高度为 \(H_i\)，满足序列 \(H\) 是 \(1,2,\cdots,N\) 的 排列。

高桥在一开始选定任意一个平台，接下来他会不停地在平台之间跳跃。假设他当前在平台 \(i\)，则他跳跃的目标平台 \(j\) 满足：

• \(1\le|i-j|\le R\)；
• \(H_j\le H_i-D\)。

可以发现，在移动有限次后，高桥将无法继续移动。

给定 \(D,R\)，求高桥移动次数的 最大值。

\(1\le N\le5\times10^5\)，\(1\le D,R\le N\)。保证 \(H_1,H_2,\cdots,H_N\) 为 \(1,2,\cdots,N\) 的一个排列。

设 \(dp_i\) 表示从平台 \(i\) 出发的最大移动次数。

显然，高桥只会从较高的平台不停往较低的平台移动，又根据 \(dp\) 数组的定义，我们应该反过来按平台的高度从小到大进行 DP。

设 \(idx_i\) 表示高度为 \(i\) 的平台的编号。设从高度为 \(i\) 的平台出发，则能一步到达的平台 \(j\) 满足：

• \(|idx_i-j|\le R\)；
• \(H_j\le i-D\)。

对于所有满足上述条件的 \(j\)，令 \(dp_{idx_i}\gets\max\{dp_{idx_i},dp_j+1\}\)。

那么如何快速找出所有满足条件的 \(j\) 呢？

在遍历的过程中，满足条件的 \(j\) 对应的 \(H_j\) 始终满足 \(H_j\le i-D\)，且 \(i\) 是单调递增的。

那么，单论高度来说，加入候选集合的 \(j\) 就是只进不出的。

而对于下标的区间，可以维护一个支持查询区间最大值的数据结构。

因此，维护一个线段树，其中存储所有满足 \(H_j\le i-D\) 的 \(dp_j\)。

设 \(L=\max\{1,idx_i-R\},R=\min\{N,idx_i+R\}\)，则状态转移方程为

\[dp_{idx_i}=\max_{\begin{gathered}L\le j\le R\\H_j\le i-D\end{gathered}}\{dp_j\}+1. \]

同时，转移之后，向线段树中加入 \(dp_{idx_{i-D+1}}\)。

时间复杂度为 \(O(N\log N)\)。

注意，线段树中的初值不能设为 \(0\)，要设为 \(-\infty\) 或者 \(-1\)，因为有 \(dp\) 值等于 \(0\) 的位置，例如一个谷点。

#include <bits/stdc++.h>
using namespace std;
int const INF = 0x3f3f3f3f;
int const N = 5e5 + 10;

inline void gmx(int &a, int b) { a = max(a, b); }

struct SegTree {
    #define ls (u << 1)
    #define rs (u << 1 | 1)
    struct Node {
        int mx;
    } tr[N << 2];
    inline void pushup(int u) {
        tr[u].mx = max(tr[ls].mx, tr[rs].mx);
        return;
    }
    void build(int u, int l, int r) {
        tr[u].mx = -INF;
        if (l == r) return;
        int mid = l + r >> 1;
        build(ls, l, mid);
        build(rs, mid + 1, r);
        return;
    }
    void modify(int u, int l, int r, int x, int v) {
        if (l == r) return gmx(tr[u].mx, v), void();
        int mid = l + r >> 1;
        if (x <= mid) modify(ls, l, mid, x, v);
        else modify(rs, mid + 1, r, x, v);
        return pushup(u);
    }
    int query(int u, int l, int r, int ql, int qr) {
        if (ql <= l && r <= qr) return tr[u].mx;
        int mid = l + r >> 1;
        int ans = -INF;
        if (ql <= mid) gmx(ans, query(ls, l, mid, ql, qr));
        if (qr > mid)  gmx(ans, query(rs, mid + 1, r, ql, qr));
        return ans;
    }
} T;

signed main() {
    cin.tie(0)->sync_with_stdio(false);

    int n, d, r;
    cin >> n >> d >> r;
    T.build(1, 1, n);
    vector<int> h(n + 1), idx(n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> h[i];
        idx[h[i]] = i;
    }
    vector<int> dp(n + 1, 0);
    for (int i = 1; i <= n; i++) {
        if (i > d) T.modify(1, 1, n, idx[i - d], dp[idx[i - d]]);
        int L = max(1, idx[i] - r);
        int R = min(n, idx[i] + r);
        gmx(dp[idx[i]], T.query(1, 1, n, L, R) + 1);
    }
    cout << *max_element(dp.begin(), dp.end());

    return 0;
}