POI - A

POI - A

知识点：

A. 旋转变换坐标公式，Dilworth 定理

B. 贪心

C. 二项式定理，特殊性质，Lucas 定理

D. 阶梯博弈(Staircase Nim)

E. 扫描线

F. 单调队列优化 DP

G. 差分约束，Tarjan 缩点，Floyd 最短路

H. 树上 DP，二分答案

I. 单调栈

J. AC 自动机

A. [POI 1998] Flat Broken Lines (lam)

SZKOpuł | 洛谷 P5939 | 码创未来

题意

给定坐标系上的 \(n\) 个格点，现在画一些折线，使所有点都在某一条折线上。要求一条折线只能从左边到右边一笔画过去，并且折线的每一段和 \(x\) 轴的夹角在 \([-45^\circ,45^\circ]\) 之间。求最少的折线数。

对于 \(100\%\) 的数据，\(1\le n\le30000\)，\(0\le x,y\le 30000\)。

思路

夹角区间 \([-45^\circ,45^\circ]\) 不好处理，我们把所有点绕坐标原点逆时针旋转 \(45^\circ\)，那么夹角区间就变成了 \([0,90^\circ]\)。

旋转变换坐标公式：将点 \((x,y)\) 绕原点旋转 \(\theta\) 角，所得的点为 \((x\cos\theta-y\sin\theta,y\cos\theta+x\sin\theta)\)。

这里 \(\theta=45^\circ\)，所以 \((x_i,y_i)\) 旋转后的坐标为 \(\left(\dfrac{\sqrt2}2x_i-\dfrac{\sqrt2}2y_i,\dfrac{\sqrt2}2y_i+\dfrac{\sqrt2}2x_i\right)\)。

由于系数不影响相对位置，所以我们最后记录的点就是 \((x_i-y_i,x_i+y_i)\)。

观察夹角区间，发现如果把点按 \(x\) 坐标从小到大排序，那么每一条折线就是所有 \(y\) 坐标的一个单调不下降子序列。

于是我们先将点按横坐标排序，然后计算 \(y\) 坐标构成的数组的最少单调不下降子序列个数。

Dilworth 定理：

• 一个数列的最少单调不上升子序列个数等于最长单调上升子序列长度；

• 一个数列的最少单调不下降子序列个数等于最长单调下降子序列长度。

有了这个定理，问题就变成了我们熟悉的求最长下降子序列长度了。

代码

#include <iostream>
#include <algorithm>
#define f(x, y, z) for (int x = (y); (x) <= (z); ++(x))
using namespace std;
const int N = 3e4 + 10;
int n, ans, f[N];

struct Point {
    int x, y;
    friend bool operator<(Point const &p, Point const &q) {
        return p.x == q.x ? p.y < q.y : p.x < q.x;
    }
} a[N];

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    
    cin >> n;
    f(i, 1, n) {
        int x, y;
        cin >> x >> y;
        a[i] = (Point){x - y, x + y};
    }
    sort(a + 1, a + n + 1);
    f[ans = 1] = a[1].y;
    f(i, 2, n)
        if (a[i].y < f[ans]) f[++ans] = a[i].y;
        else f[lower_bound(f + 1, f + ans + 1, a[i].y, greater<int>()) - f] = a[i].y;
    cout << ans << '\n';
    
    return 0;
}

B. [POI 2003] Chocolate (cze)

SZKOpuł | 洛谷 P5948 | 码创未来

题意

有一块 \(n\times m\) 的矩形巧克力，准备将它切成 \(n\times m\) 块。

巧克力上共有 \(n-1\) 条横线和 \(m-1\) 条竖线，你每次可以沿着其中的一条横线或竖线将巧克力切开，无论切割的长短，沿着每条横线切一次的代价依次为 \(y_1,y_2,\dots,y_{n-1}\)，而沿竖线切割的代价依次为 \(x_1,x_2,\dots,x_{m-1}\)。例如，对于下图 \(6\times4\) 的巧克力：

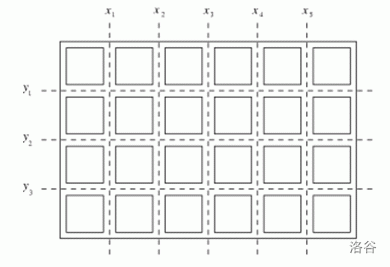
我们先沿着三条横线切割，需要 \(3\) 刀，得到 \(4\) 条巧克力，然后再将这 \(4\) 条巧克力沿同一条竖线切割，每条都需要 \(5\) 刀，则最终所花费的代价为 \(y_1+y_2+y_3+4\times (x_1+x_2+x_3+x_4+x_5)\)。

当然，上述简单切法不见得是最优切法，那么怎样切割该块巧克力，花费的代价最少呢？

思路

首先可以发现：如果选择横着切，那么如果当前已经竖着切了 \(a\) 次（不论沿哪些条竖线），则代价就乘以 \(a\)。选择竖着切同理。

设当前竖着切了 \(a\) 次，横着切了 \(b\) 次。对于每次切割，\(a\) 和 \(b\) 一定是不会减少的，所以不论横着还是竖着，代价越大就越应该先切。可以用调整法证明。

所以我们将 \(x\) 和 \(y\) 数组放到一起排序，模拟切割的过程即可。

代码

#include <iostream>
#include <algorithm>
#define f(x, y, z) for (int x = (y); (x) <= (z); ++(x))
#define int ll
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 2e4 + 10;
int n, m, ans, x, y;
pii a[N];

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    
    cin >> n >> m;
    f(i, 1, n - 1) cin >> a[i].first, a[i].second = 0;
    f(i, n, n + m - 2) cin >> a[i].first, a[i].second = 1;
    n = n + m - 2;
    sort(a + 1, a + n + 1, [](pii const &p, pii const &q) { return p.first > q.first; });
    f(i, 1, n)
        if (a[i].second == 0) ans += a[i].first * (y + 1), ++x;
        else ans += a[i].first * (x + 1), ++y;
    cout << ans << '\n';
    
    return 0;
}

C. [POI 2003] Trinomial (tro)

SZKOpuł | 洛谷 P5947 | 码创未来

题意

求 \((x^2+x+1)^n\) 的第 \(i\) 次项系数 \(\bmod3\) 的结果。

对于 \(100\%\) 的数据，\(1 \le k \le 10000\)，\(0\le n\le 10^{15}\)，\(0\le i\le 2\times n\)。

思路

此题的一个重要特殊性质就是对 \(3\) 取余。

我们可以把原式的每项系数尽量变成带 \(3\) 的形式：

\[\begin{aligned} &(x^2+x+1)^n\\ =&((x-1)^2+3x)^n\\ =&\sum_{t=0}^n\binom nt(x-1)^{2t}\times(3x)^{n-t}. \end{aligned} \]

于是我们只需要考虑 \(\dbinom nn(x-1)^{2n}=(x-1)^{2n}\) 中次数为 \(i\) 的项的系数。

\[\begin{aligned} &(x-1)^{2n}\\ =&\sum_{i=0}^{2n}\binom{2n}ix^i(-1)^{2n-i}. \end{aligned} \]

所以次数为 \(i\) 的项的系数为 \(\dbinom{2n}i(-1)^{2n-i}\)。

代码

#include <iostream>
#define f(x, y, z) for (int x = (y); (x) <= (z); ++(x))
#define il inline
#define int long long
using namespace std;
const int MOD = 3;
int f[5][5];

il int C(int n, int m) {
    if (n < m) return 0;
    return f[n][m];
}

int Lucas(int n, int m) {
    if (n < m) return 0;
    if (n == m || m == 0) return 1;
    if (m == 1) return n;
    return Lucas(n / MOD, m / MOD) * C(n % MOD, m % MOD) % MOD;
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    
    int k, n, i;
    cin >> k;
    f[0][0] = 1;
    f(i, 1, 2) {
        f[i][0] = 1;
        f(j, 1, i) f[i][j] = f[i - 1][j - 1] + f[i - 1][j];
    }
    while (k--) {
        cin >> n >> i;
        cout << (Lucas(n << 1, i) * (((n * 2 - i) & 1) ? -1 : 1) % MOD + MOD) % MOD << '\n';
    }
    
    return 0;
}

D. [POI 2004] Game (gra)

见我的另一篇文章 学习笔记：Nim 游戏。

E. [POI 2001] Goldmine (kop)

SZKOpuł | 洛谷 P8370 | 码创未来

题意

平面内有 \(n\) 个坐标为整数的点，求用一个 \(s\times w\) 的矩形能覆盖的点的个数的最大值（在矩形的边上也算覆盖）。

对于 \(100\%\) 的数据，\(1 \le s,w \le 10000,1 \le n \le 15000,-30000 \le x,y \le 30000\)。

思路

类似 洛谷 P1502 窗口的星星 的思想。

以每一个点为左下角顶点，画一个 \(s\times w\) 的矩形 \(A\)，那么放置的矩形能够覆盖这个点当且仅当矩形的右上角顶点在矩形 \(A\) 内。

于是答案即为所有矩形 \(A\) 最多重叠的层数。做一次扫描线即可求出。

代码

#include <iostream>
#include <algorithm>
#define f(x, y, z) for (int x = (y); (x) <= (z); ++(x))
using namespace std;
const int N = 1e5 + 10;
int s, w, n, ans;

struct Q {
    int x, sy, ty, c;
    Q() {}
    Q(int _x, int _sy, int _ty, int _c): x(_x), sy(_sy), ty(_ty), c(_c) {}
    friend bool operator<(Q const &_, Q const __) {
        return _.x == __.x ? _.c > __.c : _.x < __.x;
    }
} q[N];

struct SegTree {
    #define lson (u << 1)
    #define rson (u << 1 | 1)
    struct Node {
        int l, r, add, maxx;
        Node() {}
        Node(int _l, int _r): l(_l), r(_r), add(0), maxx(0) {}
    } tr[N << 2];
    void pushup(int u) {
        tr[u].maxx = max(tr[lson].maxx, tr[rson].maxx);
        return;
    }
    void pushdown(int u) {
        if (tr[u].add) {
            Node &rt = tr[u], &ls = tr[lson], &rs = tr[rson];
            ls.add += rt.add, ls.maxx += rt.add;
            rs.add += rt.add, rs.maxx += rt.add;
            rt.add = 0;
        }
        return;
    }
    void build(int u, int l, int r) {
        tr[u] = Node(l, r);
        if (l == r) return;
        int mid = (l + r) >> 1;
        build(lson, l, mid);
        build(rson, mid + 1, r);
        // pushup(u);
        return;
    }
    void modify(int u, int l, int r, int x) {
        if (l <= tr[u].l && tr[u].r <= r) {
            tr[u].maxx += x, tr[u].add += x;
            return;
        }
        pushdown(u);
        int mid = (tr[u].l + tr[u].r) >> 1;
        if (l <= mid) modify(lson, l, r, x);
        if (r > mid) modify(rson, l, r, x);
        pushup(u);
        return;
    }
} t;

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    
    cin >> s >> w >> n;
    f(i, 1, n) {
        int x, y;
        cin >> x >> y;
        x += 30001, y += 30001;
        q[(i << 1) - 1] = Q(x, y, y + w, 1);
        q[i << 1] = Q(x + s, y, y + w, -1);
    }
    n <<= 1;
    sort(q + 1, q + n + 1);
    t.build(1, 1, 60001);
    f(i, 1, n) {
        ans = max(ans, t.tr[1].maxx);
        t.modify(1, q[i].sy, q[i].ty, q[i].c);
    }
    cout << ans << '\n';
    
    return 0;
}

F. [POI 2014] Little Bird (pta)

SZKOpuł | 洛谷 P3572 | 码创未来

题意

有 \(n\) 棵树排成一排，第 \(i\) 棵树的高度是 \(d_i\)。有 \(q\) 只鸟要从第 \(1\) 棵树到第 \(n\) 棵树。

当第 \(i\) 只鸟在第 \(j\) 棵树时，它可以飞到第 \(j+1, j+2, \cdots, j+k_i\) 棵树。

如果一只鸟飞到一颗高度大于等于当前树的树，那么它的劳累值会增加 \(1\)，否则不会。

请你求出每只鸟最小的劳累值。

\(1\le n\le10^6\)，\(1 \le d_i \le 10^9\)，\(1 \le q \le 25\)，\(1 \le k_i \le n - 1\)。

思路

其实 \(q\) 只鸟就是 \(q\) 组测试数据，每组数据给定 \(k\)。

设 \(f_i\) 表示在第 \(i\) 棵树的最小劳累值。容易写出 \(f_i=\min\limits_{i-k\le j<i}\{f_j+[d_i\ge d_j]\}\)。

这道题的关键就在于 \([d_i\ge d_j]\) 的贡献只有 \(0\) 或 \(1\)。

我们考虑用单调队列维护这个最小值。

设队尾为 \(t\)，如果 \(f_i<f_t\) 或者 \(f_i=f_t\wedge d_i\ge d_t\)，说明 \(i\) 比 \(t\) 不会更劣，于是 \(t\) 可以出队。

原因是 \(f_i<f_t\iff f_i+1\le f_t\)，即对于任意 \(i'\) 都有 \(f_i+[d_{i'}\ge d_i]\le f_t+[d_{i'}\ge d_i]\)。

代码

#include <iostream>
#define f(x, y, z) for (int x = (y); (x) <= (z); ++(x))
using namespace std;
const int N = 1e6 + 10;
int n, d[N], Q, k, f[N];
int q[N], h, t;

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    
    cin >> n;
    f(i, 1, n) cin >> d[i];
    cin >> Q;
    while (Q--) {
        cin >> k;
        h = t = 1;
        q[h] = 1;
        f[1] = 0;
        f(i, 2, n) {
            while (h <= t && q[h] < i - k) ++h;
            f[i] = f[q[h]] + (d[q[h]] <= d[i]);
            while (h <= t && (f[q[t]] > f[i] || (f[q[t]] == f[i] && d[i] >= d[q[t]]))) --t;
            q[++t] = i;
        }
        cout << f[n] << '\n';
    }
    
    return 0;
}

G. [POI 2012] Festival (fes)

SZKOpuł | 洛谷 P3530 | 码创未来

题意

越野赛有 \(n\) 个参赛者，给出 \(m_1\) 个二元关系 \((a,b)\) 表示 \(a\) 比 \(b\) 恰好快 \(1\) 秒，\(m_2\) 个二元关系 \((c,d)\) 表示 \(c\) 的成绩不比 \(d\) 差。

求所有参赛者一共最多可以达到多少种不同的成绩。

对于 \(100\%\) 的数据，\(2 \le n \le 600\)，\(1 \le m_{1} + m_{2} \le {10}^5\)。

思路

考虑差分约束，设 \(i\) 的成绩为 \(x_i\)。

\((a,b)\Longrightarrow x_a=x_b-1\Longrightarrow\begin{cases}x_a\le x_b-1,\\x_b\le x_a+1,\end{cases}\) 于是由 \(a\) 向 \(b\) 连权值为 \(1\) 的边，由 \(b\) 向 \(a\) 连权值为 \(-1\) 的边。

\((c,d)\Longrightarrow x_c\le x_d+0\)，于是由 \(d\) 向 \(c\) 连权值为 \(0\) 的边。

首先无解情况就是图中有负环的情况，可以用 Floyd 算法判断：如果做完 Floyd 之后存在 \(dis(i,i)<0\)，那么说明存在负环。

那么如何求出答案呢？首先，对于任何一个 SCC，所有人的时间都加上同一个值对相互间的关系没有影响，而两个 SCC 之间的边一定是 \((c,d)\) 权值为 \(0\) 的边，所以我们可以求出每个 SCC 中的答案然后求和。

于是考虑单独一个 SCC。求最多的不同的成绩数，即是求最长的最短路长度再加一。先用 Floyd 处理所有最短路，然后枚举求出最大值，累加进答案。

代码

洛谷上开了 O2 优化才过的。

#include <iostream>
#include <cstring>
#include <vector>
#define f(x, y, z) for (int x = (y); (x) <= (z); ++(x))
#define pb push_back
using namespace std;
typedef vector<int> vi;
const int N = 610, M = 1e5 + 10;
int n, m1, m2, ans, x, y;
int dis[N][N];

vi e[N];
inline void add(int u, int v, int w) {
    e[u].pb(v);
    dis[u][v] = min(dis[u][v], w);
    return;
}

int dfn[N], low[N], tot;
int st[N], top;
vector<vi> scc;
bool inStack[N];
void Tarjan(int u) {
    dfn[u] = low[u] = ++tot;
    inStack[st[++top] = u] = true;
    for (auto v: e[u])
        if (!dfn[v]) Tarjan(v), low[u] = min(low[u], low[v]);
        else if (inStack[v]) low[u] = min(low[u], dfn[v]);
    if (dfn[u] == low[u]) {
        scc.pb(vi());
        int t;
        while (true) {
            t = st[top--];
            inStack[t] = false;
            scc.back().pb(t);
            if (t == u) break;
        }
    }
    return;
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    
    memset(dis, 0x3f, sizeof dis);
    cin >> n >> m1 >> m2;
    f(i, 1, n) dis[i][i] = 0;
    f(i, 1, m1) cin >> x >> y, add(y, x, -1), add(x, y, 1);
    f(i, 1, m2) cin >> x >> y, add(y, x, 0);
    f(i, 1, n) if (!dfn[i]) Tarjan(i);
    f(k, 1, n) f(i, 1, n) f(j, 1, n)
        dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
    f(i, 1, n) if (dis[i][i]) return cout << "NIE\n", 0;
    for (auto i: scc) {
        int maxx = 0;
        for (auto u: i) for (auto v: i)
            maxx = max(maxx, dis[u][v]);
        ans += maxx + 1;
    }
    cout << ans << '\n';
    
    return 0;
}

H. [POI 2011] Dynamite (dyn)

SZKOpuł | 洛谷 P3523 | 码创未来

题意

给定一棵 \(n\) 个节点的树，其中有一些关键节点。现在要在树上选择 \(m\) 个节点（不一定是关键节点）。

设一个关键节点 \(i\) 到所有选定节点的距离最小值为 \(f(i)\)。求出 \(\max f(i)\) 的最小值。

\(1\le m\le n\le300000\)。

思路

首先我们对答案进行二分。设当前二分的答案为 \(x\)。

那么问题转化为：一棵树上选 \(m\) 个点，使得这 \(m\) 个点与关键节点的最小距离不超过 \(x\)。

然后发现这个问题并不容易解决，于是问题还可以进一步转化：一棵树上选 \(tot\) 个点，使得这 \(tot\) 个点与关键节点的最小距离不超过 \(x\)，最小化 \(tot\)。

即用最少的点覆盖所有关键节点。

设 \(f_i\) 表示 \(i\) 子树内最远的未被覆盖的 关键点 与 \(i\) 的距离，\(g_i\) 表示 \(i\) 子树内最近的被选择的节点与 \(i\) 的距离。

\(f\) 初始值为 \(-\infty\)， \(g\) 初始值为 \(+\infty\)。若 \(u\) 为关键节点，则 \(f_u\) 初始值为 \(0\)。

设 \(v\) 为 \(u\) 的儿子，那么 \(f_u=\max f_v+1,g_u=\min g_v+1\)。

如果 \(f_u+g_u\le x\)，说明 \(u\) 子树内的关键节点都可以被覆盖，所以可以忽略掉，于是令 \(f_u=-\infty\)；

否则，如果 \(f_u=x\)，说明必须要选择 \(u\) 了，于是令 \(f_u=-\infty,g_u=0\)。

注意：特判根节点的情况。由于上面没有更优的点可以选了，所以如果还有没被覆盖的关键节点即 \(f_{rt}>0\)，那么选择 \(rt\)。

代码

#include <iostream>
#define f(x, y, z) for (int x = (y); (x) <= (z); ++(x))
#define il inline
using namespace std;
const int N = 3e5 + 10;
const int INF = 0x3f3f3f3f;
int n, m;
bool a[N];

int head[N], cnt;
struct Edge {
    int to, nxt;
} e[N << 1];
il void add(int from, int to) {
    e[++cnt].to = to, e[cnt].nxt = head[from], head[from] = cnt;
    return;
}

int tot;
int f[N], g[N]; //f[i]: 以i为根的子树中最远未覆盖节点距离; g[i]: 以i为根的子树中最近选择节点距离
void dfs(int u, int fa, int limit) {
    f[u] = a[u] ? 0 : -INF;
    g[u] = INF;
    for (int i = head[u]; i; i = e[i].nxt) {
        int v = e[i].to;
        if (v == fa) continue;
        dfs(v, u, limit);
        f[u] = max(f[u], f[v] + 1);
        g[u] = min(g[u], g[v] + 1);
    }
    if (f[u] + g[u] <= limit) f[u] = -INF; //以u为根的子树可以全部覆盖
    if (f[u] == limit) ++tot, f[u] = -INF, g[u] = 0; //选择u
    return;
}

il bool check(int x) {
    tot = 0;
    dfs(1, 0, x);
    tot += (f[1] >= 0);
    return tot <= m;
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    
    cin >> n >> m;
    f(i, 1, n) cin >> a[i];
    f(i, 1, n - 1) {
        int u, v;
        cin >> u >> v;
        add(u, v), add(v, u);
    }
    int l = -1, r = n;
    while (l + 1 < r) {
        int mid = (l + r) >> 1;
        if (check(mid)) r = mid;
        else l = mid;
    }
    cout << r << '\n';
    
    return 0;
}

I. [POI 2008] Postering (pla)

SZKOpuł | 洛谷 P3467 | 码创未来

题意

\(n\) 个矩形，排成一排，现在希望用尽量少的大矩形覆盖住它们。如下图：

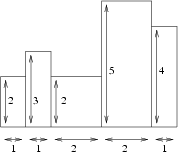
思路

显然矩形的宽度无用。

我们发现一个“凹”字形需要用三张海报，而“凸”字形却可以减少一张。

所以前面比当前矩形高的所有矩形都是没有用的。

令初始答案为 \(n\)，如果发现当前矩形可以形成“凸”字形，那么答案减一。

具体来说，我们维护一个单调栈，如果栈顶矩形比当前矩形高，那么将栈顶弹出；如果栈顶矩形与当前矩形等高，那么答案减一。

代码

#include <iostream>
#include <stack>
#define f(x, y, z) for (int x = (y); (x) <= (z); ++(x))
using namespace std;
int n, ans;
stack<int> st;

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    
    cin >> n;
    ans = n;
    f(i, 1, n) {
        int h, w;
        cin >> w >> h;
        while (!st.empty() && st.top() >= h) {
            if (st.top() == h) --ans;
            st.pop();
        }
        st.push(h);
    }
    cout << ans << '\n';
    
    return 0;
}

J. [POI 2000] Viruses (wir)

SZKOpuł | 洛谷 P2444 | 码创未来

TO DO...