10.25 L5-noip训练3 题解

L5-noip训练3 题解

A. tile（gcd）

题意

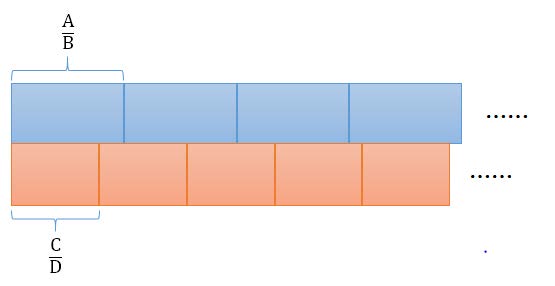
如上图所示，两排瓷砖长度分别为 \(\frac AB\) 和 \(\frac CD\)，从同一起始位置开始向右排列，两排瓷砖的第一块的左端的缝隙是对齐的。

你想要知道，最短铺多少距离后，两排瓷砖的缝隙会再一次对齐。

思路

求“两个分数的 \(\operatorname{lcm}\)”。我们先把两个分数通分，求一下分子的 \(\operatorname{lcm}\)，再约分输出即可。

代码

#include <cstdio>
#include <iostream>
#include <algorithm>
#define FILENAME "tile"
#define int ll
using namespace std;
typedef long long ll;
int const N = 1e5 + 10;
int T, a, b, c, d;
int fenzi, fenmu;

inline int lcm(int x, int y) { return x / __gcd(x, y) * y; }

void print() {
	int g = __gcd(fenzi, fenmu);
	fenzi /= g, fenmu /= g;
	if (fenzi == 0) cout << 0 << '\n';
	else if (fenmu == 1) cout << fenzi << '\n';
	else cout << fenzi << '/' << fenmu << '\n';
	return;
}

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);
	freopen(FILENAME".in", "r", stdin);
	freopen(FILENAME".out", "w", stdout);
	
	cin >> T;
	while (T--) {
		cin >> a >> b >> c >> d;
		fenmu = lcm(b, d);
		a *= fenmu / b;
		c *= fenmu / d;
		fenzi = lcm(a, c);
		print();
	}
	
	return 0;
}

B. question（树上问题）

题意

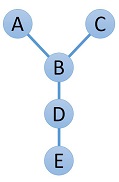
给定一棵树，求“ Y 字形”（如上图所示）的数量，以及所有“ Y 字形”的边权和中的最大值。

思路

可以将 Y 字形看做是中间的节点（图中的 \(B\)）分三叉，其中两叉长度为 \(1\)，一叉长度为 \(2\)。

显然度数至少为 \(3\) 才可以是中间节点。并且对于一个中间节点的相邻节点，度数至少为 \(2\) 才可以是长度为 \(2\) 的那一叉（图中的 \(D\)）。

• 首先考虑如何求第一问 Y 字形的数量。

  记录所有节点的度数 \(deg\)。

  枚举所有度数大于等于 \(3\) 的节点 \(u\)，枚举与该节点相邻的度数大于等于 \(2\) 的节点 \(v\)。

  那么图中的 \(A,C\) 的种类数为 \(\dbinom{deg_u-1}2\)，图中的 \(E\) 的种类数为 \(deg_v-1\)。

  根据乘法原理，\(u\) 对答案的贡献为 \(\dbinom{deg_u-1}2\times(deg_v-1)\)。

• 然后考虑如何求第二问所有 Y 字形的最大边权和。

  同样枚举所有度数大于等于 \(3\) 的节点 \(u\) 和与该节点相邻的度数大于等于 \(2\) 的节点 \(v\)。

  对于 \(u\)，令边权和最大的边权（图中的 \((u,A),(u,C)\)）一定是与 \(u\) 相连的边权中除了 \((u,v)\) 之外的最大值和次大值。

  同理，对于 \(v\)，令边权和最大的边权（图中的 \((v,E)\)）一定是与 \(v\) 相连的边权中除了 \((v,u)\) 之外的最大值。

  但是由于图中的 \(B-D\) 可能把与 \(u\) 相连的最大边或次大边占用，\(D-B\) 可能把与 \(v\) 相连的最大边占用，所以我们还需要记录第三大边。

  记录与每个点 \(i\) 相连的边权中的最大值、次大值、第三大值，分别用 \(f(i,0/1/2)\) 表示。

  接下来分类讨论：

  如果 \((u,v)\) 为与 \(u\) 相连的最大边权，那么用与 \(u\) 相连的次大边权和第三大边权作为 Y 字形的一部分；

  如果 \((u,v)\) 为与 \(u\) 相连的次大边权，那么用与 \(u\) 相连的最大边权和第三大边权作为 Y 字形的一部分；

  否则，用与 \(u\) 相连的最大边权和次大边权作为 Y 字形的一部分。

  如果 \((v,u)\) 为与 \(v\) 相连的最大边权，那么用与 \(v\) 相连的次大边权作为 Y 字形的一部分；

  否则，用与 \(v\) 相连的最大边权作为 Y 字形的一部分。

  然后别忘了加上 \(B-D\) 这条边。打擂台更新答案。

代码

#include <cstdio>
#include <iostream>
#define f(x, y, z) for (int x = (y); (x) <= (z); ++(x))
#define il inline
#define int ll
#define FILENAME "question"
using namespace std;
typedef long long ll;
const int N = 2e5 + 10;
int n, ans1, ans2;
int deg[N], f[N][3];

int head[N], cnt;
struct Edge {
	int to, nxt, val;
} e[N << 1];
il void add(int u, int v, int w) {
	e[++cnt].to = v, e[cnt].nxt = head[u], e[cnt].val = w, head[u] = cnt;
	++deg[u];
	if (w > f[u][0])
		f[u][2] = f[u][1], f[u][1] = f[u][0], f[u][0] = w;
	else if (w > f[u][1])
		f[u][2] = f[u][1], f[u][1] = w;
	else if (w > f[u][2])
		f[u][2] = w;
	return;
}

il int Cn2(int x) { return x * (x - 1) / 2; }

int work(int u, int v, int w) {
	ans1 += Cn2(deg[u] - 1) * (deg[v] - 1);
	if (w == f[u][0]) {
		if (w == f[v][0]) return f[u][1] + f[u][2] + f[v][1];
		else return f[u][1] + f[u][2] + f[v][0];
	} else if (w == f[u][1]) {
		if (w == f[v][0]) return f[u][0] + f[u][2] + f[v][1];
		else return f[u][0] + f[u][2] + f[v][0];
	} else {
		if (w == f[v][0]) return f[u][0] + f[u][1] + f[v][1];
		else return f[u][0] + f[u][1] + f[v][0];
	}
}

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);
	freopen(FILENAME".in", "r", stdin);
	freopen(FILENAME".out", "w", stdout);
	
	cin >> n;
	f(i, 1, n - 1) {
		int u, v, w;
		cin >> u >> v >> w;
		add(u, v, w), add(v, u, w);
	}
	f(u, 1, n)
		if (deg[u] >= 3)
			for (int i = head[u]; i; i = e[i].nxt) {
				int v = e[i].to, w = e[i].val;
				if (deg[v] >= 2)
					ans2 = max(ans2, w + work(u, v, w));
			}
	cout << ans1 << '\n' << ans2 << '\n';
	
	return 0;
}

C. plumber（搜索）

题意

你需要在一个长方体状的房间内连接一条贯穿房间内部的水管。房间的长为 \(X\)，宽为 \(Y\)，高为 \(Z\)，整个房间可以看成是\(X\times Y\times Z\)个小立方体空间组成的。

如果在房间中建立直角坐标系，则房间内每个小立方体空间都可以用一个三维坐标 \((x,y,z)\) 表示，房间一角的小立方体的坐标为 \((1,1,1)\)，它的对角的坐标为 \((X,Y,Z)\)，其余小立方体的坐标的三个维度都分别落在 \(1…X\)，\(1…Y\) 和 \(1…Z\) 内。

下图展示了房间的立方体空间的划分方式和一种开凿水管出入口的方式。

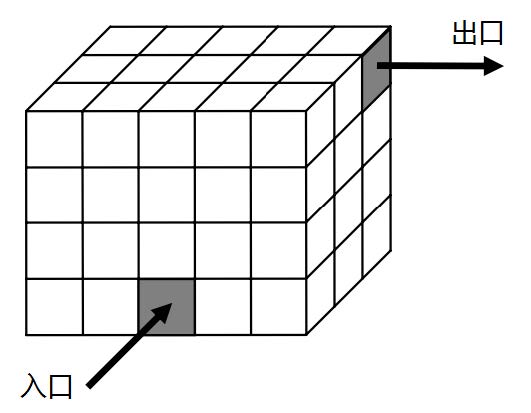
你的手头只有一种形状的水管部件，它呈 L 型，且正好占据了 \(4\) 个小立方体空间，如下图所示，灰色部分是水管部件两端的开口位置。

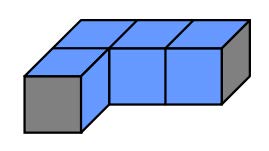
你可以任意旋转、翻转水管部件，然后将它的开口接到入口、出口或者其它水管部件的开口上。

下图展示了一种两个水管部件的连接方式。

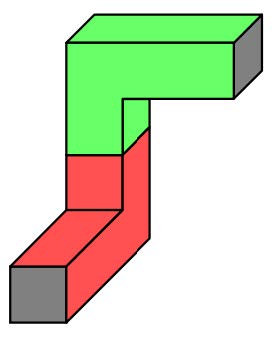
在连接水管时，水管部件间不能相交，也不能伸出房间之外。房间内有一些小立方体空间已经被物品占据了，水管也不能经过那些格子。另外，水管部件数量有限，你的手头只有 \(12\) 个这样的零件。

现在，给出房间的长、高、宽，以及入口、出口的位置和房间内物品的坐标，请你计算至少需要多少个这样的水管部件才能完成任务，或者判断无法完成任务。

对于 \(30\%\) 的数据，\(1\le X,Y,Z\le5\)；

对于 \(50\%\) 的数据，\(1\le X,Y,Z\le10\)；

对于 \(70\%\) 的数据，\(1\le X,Y,Z\le15\)；

对于 \(100\%\) 的数据，\(1\le X,Y,Z\le20\)。

思路

对于这种条件复杂、难以描述状态、数据范围很小的题，我们一般采用搜索解决。

DFS 过程中记录上一个水管的接口位置与朝向。注意起点的接口位置要向房间外面移动一格。

首先，不管水管的摆放如何，一定要向上一个水管接口的朝向铺两格。

然后，枚举短柄接上一个水管还是长柄接上一个水管。

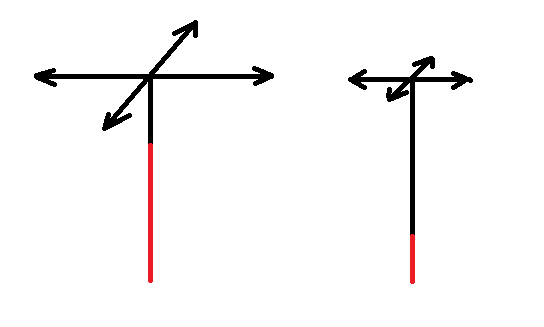
如果是短柄，那么枚举除了上一个接口朝向外的四个方向，并向各个方向铺两格。

如果是长柄，那么先向上一个水管的接口方向再铺一格，再枚举四个方向铺一格。

如上图所示，红色的是上一个水管，黑色的是当前可以铺的水管。

现在考虑如何优化 DFS。

由于答案求的是最少的水管个数，所以我们可以进行最优性剪枝。

如果当前使用的水管个数已经大于了当前最少的水管个数，那么当前方案不可能更新答案，直接 return。

但是仅仅这样还是不够，我们需要继续利用估价函数进行最优性剪枝。

考虑到每一个水管占用 \(4\) 格，我们可以求出当前点到终点的曼哈顿距离 \(dis\)，那么 \(\left\lceil\dfrac{dis}4\right\rceil\) 即为最少还需要的水管数。

如果当前水管数加上最少还需要的水管数仍然大于当前的答案，那么 return。

并且，由于水管数不超过 \(12\)，我们还可以使用迭代加深的技巧，DFS 时限制能使用的水管数量，每次不断放宽限制。

这样就可以愉快地在时限内通过本题了。

代码

#include <cstdio>
#include <iostream>
#include <cstring>
#define f(x, y, z) for (int x = (y); (x) <= (z); ++(x))
#define g(x, y, z) for (int x = (y); (x) >= (z); --(x))
#define il inline
#define FILENAME "plumber"
using namespace std;
const int N = 21;
const int dx[6] = {1, -1, 0, 0, 0, 0};
const int dy[6] = {0, 0, 1, -1, 0, 0};
const int dz[6] = {0, 0, 0, 0, 1, -1};
int X, Y, Z, m, ans = 13;
int sx, sy, sz, sf, tx, ty, tz, tf; //sf/tf: 朝向(0:+x 1:-x 2:+y 3:-y 4:+z 5:-z)
bool vis[N][N][N];
bool ok;

il bool ck(int x, int y, int z) {
	if (x >= 1 && x <= X && y >= 1 && y <= Y && z >= 1 && z <= Z && !vis[x][y][z])
		return true;
	return false;
}

il int dis(int x, int y, int z) { //计算与终点的 Manhattan 距离
	return abs(x - tx) + abs(y - ty) + abs(z - tz);
}

void dfs(int d, int x, int y, int z, int f, int limit) {
	if (ok) return;
	if ((dis(x, y, z) + 3) / 4 + d > limit) return;
	if (x == tx && y == ty && z == tz && f == tf) {
		ok = true;
		return;
	}

	if (!ck(x + dx[f], y + dy[f], z + dz[f]) || !ck(x + dx[f] * 2, y + dy[f] * 2, z + dz[f] * 2)) return;
	vis[x + dx[f]][y + dy[f]][z + dz[f]] = 1;
	vis[x + dx[f] * 2][y + dy[f] * 2][z + dz[f] * 2] = 1;

	int xx, yy, zz, xxx, yyy, zzz;
	f(i, 0, 5) {
		if (i / 2 == f / 2) continue;
		xx = x + dx[f] * 2 + dx[i], yy = y + dy[f] * 2 + dy[i], zz = z + dz[f] * 2 + dz[i];
		xxx = xx + dx[i], yyy = yy + dy[i], zzz = zz + dz[i];
		if (ck(xx, yy, zz) && ck(xxx, yyy, zzz)) {
			vis[xx][yy][zz] = vis[xxx][yyy][zzz] = 1;
			dfs(d + 1, xxx, yyy, zzz, i, limit);
			vis[xx][yy][zz] = vis[xxx][yyy][zzz] = 0;
		}
	}
	
	xxx = x + dx[f] * 3, yyy = y + dy[f] * 3, zzz = z + dz[f] * 3;
	if (ck(xxx, yyy, zzz)) {
		vis[xxx][yyy][zzz] = 1;
		f(i, 0, 5) {
			if (i / 2 == f / 2) continue;
			xx = xxx + dx[i], yy = yyy + dy[i], zz = zzz + dz[i];
			if (ck(xx, yy, zz)) {
				vis[xx][yy][zz] = 1;
				dfs(d + 1, xx, yy, zz, i, limit);
				vis[xx][yy][zz] = 0;
			}
		}
		vis[xxx][yyy][zzz] = 0;
	}
	
	vis[x + dx[f]][y + dy[f]][z + dz[f]] = 0;
	vis[x + dx[f] * 2][y + dy[f] * 2][z + dz[f] * 2] = 0;
	return;
}

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);
	freopen(FILENAME".in", "r", stdin);
	freopen(FILENAME".out", "w", stdout);
	
	char ch;
	cin >> X >> Y >> Z >> m;
	cin >> sx >> sy >> sz >> ch;
	sf = (int)(ch - 'x') * 2;
	if ((ch == 'x' && sx == X) || (ch == 'y' && sy == Y) || (ch == 'z' && sz == Z)) ++sf;
	sx -= dx[sf], sy -= dy[sf], sz -= dz[sf];
	cin >> tx >> ty >> tz >> ch;
	tf = (int)(ch - 'x') * 2;
	if ((ch == 'x' && tx == 1) || (ch == 'y' && ty == 1) || (ch == 'z' && tz == 1)) ++tf;
	f(i, 1, m) {
		int x, y, z;
		cin >> x >> y >> z;
		vis[x][y][z] = 1;
	}
	f(i, 1, 12) { //迭代加深
		dfs(0, sx, sy, sz, sf, i);
		if (ok) {
			cout << i << '\n';
			break;
		}
	}
	if (!ok) cout << "impossible\n";
	
	return 0;
}