9.7 数论测试题解

A. 取球游戏

题意

桌子上放着 \(n\) 个球，第 \(i\) 个球的编号为 \(i\)。取出 \(m\) 个球，求球的编号的最小值恰好为 \(k\) 的方案数。结果对 \(10^9 + 7\) 取模。

数据范围

\(1\le n,m\le10^6,1\le k\le n\)。

思路

不能取编号为 \(1\sim k-1\) 的球；一定取编号为 \(k\) 的球；剩下 \(n-k\) 个球中选出 \(m-1\) 个球。

所以答案为 \(\dbinom{n-k}{m-1}\)。

需要求逆元，快速幂模板省略。

代码

#include <iostream>
#define f(x, y, z) for (register int x = (y); (x) <= (z); (x)++)
using namespace std;
typedef long long ll;
const int N = 1e6 + 10;
const ll MOD = 1e9 + 7;

ll ksm(ll a, ll x) { ... }

ll C(int n, int m) {
	if (m > n) return 0;
	if (n == m) return 1;
	if (m == 0) return 1;
	ll a = 1, b = 1;
	f(i, n - m + 1, n) a = a * i % MOD;
	f(i, 2, m) b = b * i % MOD;
	return a * ksm(b, MOD - 2) % MOD;
}

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);
	
	ll n, m, k;
	cin >> n >> m >> k;
	cout << C(n - k, m - 1) << '\n';
	
	return 0;
}

B. 公约数问题

题意

给定正整数 \(n\)，请你解决下面两个子任务：

求有多少对 \((i, j)\) 满足 \(1\le i,j\le n\) 且 \(\gcd (i,j) = 1\)；
求有多少对 \((i, j)\) 满足 \(1\le i ,j\le n\) 且 \(\gcd(i,j)\) 为素数。

输入第一行为 \(T\in\{0,1\}\)，代表该测试点要完成的子任务编号。

数据范围

对于子任务 1 和 2，均有 \(1\le n\le10^7\)。

思路

子任务 1

由于 \((i,j)\) 和 \((j,i)\) 成对出现，所以只需要统计 \(j\le i\) 的情况，最后乘 \(2\) 再减 \(1\)（因为有一个 \((1,1)\) 重复计算）即为答案。

\[\begin{aligned} &\sum_{i=1}^n\sum_{j=1}^n[\gcd(i,j)=1]\\ =&2\times\sum_{i=1}^n\sum_{j=1}^i[\gcd(i,j)=1]-1\\ =&2\times\sum_{i=1}^n\varphi(i)-1. \end{aligned} \]

发现答案即为欧拉函数的前缀和。在线性筛之后处理前缀和即可。

时间复杂度 \(O(n)\)。

子任务 2

\[\begin{aligned} &\sum_{i=1}^n\sum_{j=1}^n[\gcd(i,j)\in\mathbb P]\\ =&\sum_{p\in\mathbb P}\sum_{i=1}^n\sum_{j=1}^n[\gcd(i,j)=p]\\ =&\sum_{p\in\mathbb P}\sum_{i=1}^n\sum_{j=1}^n\left[\gcd\left(\frac ip,\frac jp\right)=1\right]\\ =&\sum_{p\in\mathbb P}\left(2\times\sum_{i=1}^n\varphi\left(\frac ip\right)-1\right). \end{aligned} \]

其中 \(\mathbb P\) 表示全体质数构成的集合。

线性筛处理出 \(n\) 以内的质数后，枚举所有的质数，像子任务 1 一样求出答案并累加起来，即为所求。

代码

#pragma GCC optimize(2)
#include <iostream>
#include <bitset>
#include <cmath>
#define f(x, y, z) for (register int x = (y); (x) <= (z); (x)++)
using namespace std;
typedef long long ll;
const int N = 1e7;
int T, n;
ll ans;
bitset<N + 10> ck;
int pri[700000], cnt;
int phi[N];
ll sum[N]; //欧拉函数前缀和

inline void get_phi() {
	f(i, 2, n) {
		if (!ck[i]) pri[++cnt] = i, phi[i] = i - 1;
		f(j, 1, cnt) {
			int k = i * pri[j];
			if (k > N) break;
			ck[k] = true;
			if (!(i % pri[j])) {
				phi[k] = phi[i] * pri[j];
				break;
			}
			phi[k] = phi[i] * (pri[j] - 1);
		}
	}
	f(i, 2, n) sum[i] = sum[i - 1] + phi[i];
}

int main() {
	
	cin >> T >> n;
	get_phi();
	if (T == 1) {
		cout << (sum[n] << 1 | 1) << '\n';
	} else if (T == 2) {
		f(i, 1, cnt) ans += (sum[n / pri[i]] << 1 | 1);
		cout << ans << '\n';
	}
	
	return 0;
}

C. 那些年

题意

题目分为四个子任务：

测试点编号	子任务编号	所求问题的值
\(1\sim 8\)	\(1\)	\(ax\equiv 1\pmod p\) 的最小整数解 \(x\)
\(9\sim 12\)	\(2\)	\(a^x\equiv 1\pmod p\) 的最小整数解 \(x\)
\(13\sim 16\)	\(3\)	\(\displaystyle\sum\limits_{i=1}^n\sum\limits_{j=1}^m\gcd(i,j)\)
\(17\sim 20\)	\(4\)	\(\displaystyle\sum\limits_{i=1}^n\left\lfloor\frac ni\right\rfloor\)

数据范围

子任务 1：\(1\le a,p\le10^9,T=10^5\)，\(a\perp p\)；

子任务 2：\(1\le a,p\le10^9,T=2\times10^3\)，\(p\) 为素数且 \(a\perp p\)；

子任务 3：\(1\le n,m\le10^7,T=10^3\)；

子任务 4：\(1\le n\le10^7,T=10^5\)。

其中 \(T\) 为询问数。

对于子任务 \(1\) 和 \(2\)，输入数据保证有解。

对于全部测试数据，\(1 \le Q \le 4\)，\(Q\) 为输入的子任务编号。

思路与代码

子任务 1（扩展欧几里得算法）

exgcd 模板。

\(ax\equiv1\pmod p\iff xa+yp=1\)。用 exgcd 求出 \(x,y\) 即可。

题中要求 \(x\) 为最小正整数解，则 \(x\leftarrow(x+p)\bmod p\)。

namespace task1 {
	int exgcd(int a, int b, int &x, int &y) {
		if (!b) {
			x = 1, y = 0;
			return a;
		}
		int g = exgcd(b, a % b, x, y);
		int t = x;
		x = y;
		y = t - a / b * y;
		return g;
	}
	void solve1() {
		while (T--) {
			int x, y, a, b;
			cin >> a >> b;
			exgcd(a, b, x, y);
			cout << (x + b) % b << '\n';
		}
		return;
	}
}

时间复杂度 \(O(T\log p)\)。

子任务 2（费马小定理，试除求阶）

注意到问题的形式与费马小定理 \(a^{p-1}\equiv1\pmod p\) 颇为相似。

可不可以由 \(x_0=p-1\) 求出最小整数解呢？

猜想：若 \(a^m\equiv1\pmod p\)，且 \(a^x\equiv1\pmod p\) 的最小正整数解是 \(x\)，那么 \(x\mid m\)。

证明：假设 \(x\nmid m\)，那么可设 \(m=kx+b\)，其中 \(0<b<x\)。

于是 \(a^{kx+b}\equiv1\pmod p\)，所以 \(a^b\equiv1\pmod p\)，即存在 \(0<b<x\) 使得方程成立，与 \(x\) 为最小正整数解矛盾。因此假设不成立，原命题得证。

所以，我们只需要令 \(x=p-1\)，然后不断用 \(x\) 去除以它的最小质因子，直到 \(a^x\not\equiv1\pmod p\)，此时上一个 \(x\) 即为最小正整数解。

（代码中线性筛质数省略）

namespace task2 {
	const int N = 1e5 + 10; int pri[10000], cnt; bitset<N> ck;
	inline void get_pri() { ... }
	void solve2() {
		get_pri();
		while (T--) {
			int a, p, x;
			cin >> a >> p;
			x = p - 1;
			f(i, 1, cnt) {
				if (pri[i] > x / pri[i]) break;
				while (x % pri[i] == 0) {
					if (ksm(a, x / pri[i], p) == 1) x /= pri[i];
					else break;
				}
			}
			cout << x << '\n';
		}
		return;
	}
}

时间复杂度 \(O(T\sqrt p)\)。

子任务 3（推式子 + 数论分块）

引理：\(\displaystyle n=\sum\limits_{d\mid n}\varphi(d)\)。

证明：将正整数 \(1,2,\dots,n\) 按其和 \(n\) 的最大公约数分成若干集合。

若用 \(\tau(n)\) 表示 \(n\) 的约数个数，那么这些集合一共有 \(\tau(n)\) 个，且每一个 \(d\mid n\) 与分出的一个集合一一对应。

显然，这些集合两两互斥，且并集为 \(\{1,2,\dots,n\}\)。所以，有 \(\displaystyle n=\sum\limits_{d\mid n}\sum\limits_{i=1}^n[\gcd(i,n)=d]\)。

由 \(\gcd\) 的性质，上式等于 \(\displaystyle \sum\limits_{d\mid n}\sum\limits_{i=1}^{n}\left[\gcd\left(\dfrac id,\dfrac nd\right)=1\right]\)。

由欧拉函数的定义，上式等于 \(\displaystyle \sum\limits_{d\mid n}\varphi\left(\dfrac nd\right)\)。

由于每一个 \(d\) 都对应一个 \(\dfrac nd\)，上式即为 \(\displaystyle \sum\limits_{d\mid n}\varphi(d)\)。证毕。

（用 Dirichlet 卷积的形式讲，该结论即为：\(\operatorname{Id}=\varphi\ast1\)）

接下来大力推式子：

\[\begin{aligned} & \sum_{i=1}^n\sum_{j=1}^m\gcd(i,j)\\ =& \sum_{i=1}^n\sum_{j=1}^m\sum_{d\mid\gcd(i,j)}\varphi(d)\\ =& \sum_{i=1}^n\sum_{j=1}^m\sum_{d\mid i\wedge d\mid j}\varphi(d)\\ =& \sum_{d=1}^n\varphi(d)\sum_{i=1}^n\sum_{j=1}^m\sum_{d\mid i\wedge d\mid j}1\\ =& \sum_{d=1}^n\varphi(d)\left(\sum_{i=1}^n[d\mid i]\right)\left(\sum_{j=1}^m[d\mid j]\right)\\ =& \sum_{d=1}^n\varphi(d)\left\lfloor\frac nd\right\rfloor\left\lfloor\frac md\right\rfloor. \end{aligned} \]

先处理出欧拉函数的前缀和，然后用数论分块：算出 \(\left\lfloor\dfrac nd\right\rfloor\) 和 \(\left\lfloor\dfrac md\right\rfloor\) 均相等的每一段 \(d\) 的长度，乘以 \(\varphi(d)\) 的值并累加。

（线性筛欧拉函数并求前缀和部分省略）

namespace task3 {
	const int N = 1e7 + 10; int pri[700000], cnt, phi[N]; bitset<N> ck;
	void get_phi() { ... }
	void solve3() {
		get_phi();
		while (T--) {
			int n, m, ans = 0;
			cin >> n >> m;
			if (n > m) swap(n, m);
			int l = 1, rn, rm, r;
			while (l <= n) {
				rn = n / (n / l), rm = m / (m / l);
				r = min(rn, rm);
				ans += (phi[r] - phi[l - 1]) * (n / l) * (m / l);
				l = r + 1;
			}
			cout << ans << '\n';
		}
	}
}

时间复杂度 \(O\left(n+T\left(\sqrt n+\sqrt m\right)\right)\)。

子任务 4（变换 -> 线性筛约数个数）

结论：令 \(\tau(i)\) 表示 \(i\) 的正因数个数，那么 \(\displaystyle \sum\limits_{i=1}^n\left\lfloor\dfrac ni\right\rfloor=\sum\limits_{i=1}^n\tau(i)\)。

感性理解：

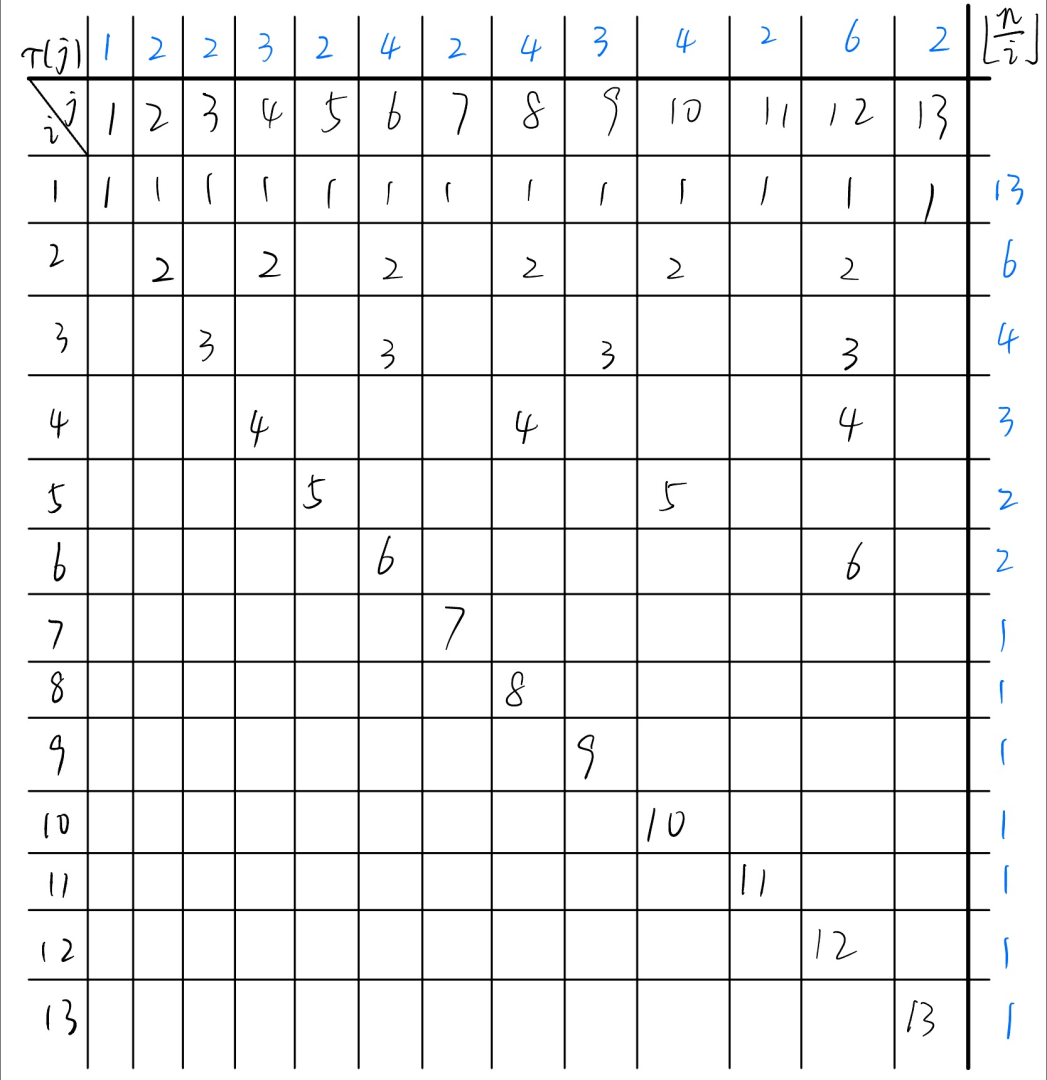
\(\displaystyle \sum\limits_{i=1}^{13}\left\lfloor\dfrac {13}i\right\rfloor=\sum\limits_{j=1}^{13}\tau(j)=37\)。

于是可以线性预处理出 \(\tau\) 的前缀和 \(s\)，输出 \(s(n)\) 即为答案。

时间复杂度 \(O(n+T)\)。

namespace task4 {
	const int N = 1e7 + 10;
	int pri[700000], cnt, t[N], g[N];
	bitset<N> ck;
	void get_tau() {
		t[1] = 1;
		f(i, 2, 1e7) {
			if (!ck[i]) pri[++cnt] = i, g[i] = t[i] = 2;
			f(j, 1, cnt) {
				int k = i * pri[j];
				if (k > 1e7) break;
				ck[k] = true;
				if (!(i % pri[j])) {
					g[k] = g[i] + 1;
					t[k] = t[i] / g[i] * (g[i] + 1);
					break;
				}
				g[k] = 2;
				t[k] = t[i] * 2;
			}
		}
		f(i, 2, 1e7) t[i] += t[i - 1];
	}
	void solve4() {
		get_tau();
		while (T--) {
			int n;
			cin >> n;
			cout << t[n] << '\n';
		}
		return;
	}
}

总结

考点：

组合数学；

欧拉函数的性质；

扩展欧几里得算法；

费马小定理；

同余的性质；

数论分块；

线性筛（质数、欧拉函数、约数个数）。

posted @ 2022-11-06 20:25 f2021ljh 阅读(16) 评论(0) 收藏举报

刷新页面返回顶部

f2021ljh's blog

Knowledge Above All Nonsenses

9.7 数论测试题解