9.2 数论测试 B. 方程 题解

方程 - 题目 - 码创未来

答案取模无高精度非毒瘤版：P1445 [Violet] 樱花

题目描述

给定一个正整数 \(n\)，找到符合下面方程的正整数解 \((x,y)\) 的数量：

\[\frac{1}{n!}=\frac{1}{x}+\frac{1}{y} \]

其中，\(n!\) 表示 \(n\) 的阶乘，即 \(n!=1\times 2\times 3\times \ldots \times n\)。

数据范围

对于 \(30\%\) 的数据，满足 \(n\le 100\)，数据不超过 10 组；

对于 \(50\%\) 的数据，满足：\(n\le 10^3\)，数据组数不超过 20 组；

对于 \(100\%\) 的数据，满足：\(n\le 10^4\)，数据组数不超过 30 组。

分析

一波大力推导式子：

\[\begin{gather*} \frac1{n!}=\frac1x+\frac1y\\ \frac1{n!}=\frac{x+y}{xy}\\ n!=\frac{xy}{x+y}\\ n!(x+y)=xy\\ n!(x+y)-xy=0 \end{gather*} \]

来自数学大佬 Raymin 的神奇因式分解：

\[\begin{gather*} 令\,a=-n!\\ a(x+y)+xy=0\\ a^2+a(x+y)+xy=a^2\\ (a+x)(a+y)=a^2\\ (x-n!)(y-n!)=(n!)^2\\ \end{gather*} \]

于是得到

\[(x-n!)\mid(n!)^2. \]

由于每一组不同的解 \((x,y)\) 都对应一个 \(x\)，每一个 \(x\) 都对应一个 \(x-n!\)，而不同的 \((x-n!)\) 的个数即为 \((n!)^2\) 的因数个数，所以求出 \((n!)^2\) 的因数个数即为答案。

设 \(n!=p_1^{\alpha_1}p_2^{\alpha_2}\dots p_k^{\alpha_k}\)，则 \((n!)^2=p_1^{2\alpha_1}p_2^{2\alpha_2}\dots p_k^{2\alpha_k}\)。

所以

\[\text{ans}=(2\alpha_1+1)(2\alpha_2+1)\dots(2\alpha_k+1). \]

那么，对于每一个质因子 \(p_i\)，如何求出对应的 \(\alpha_i\) 呢？

下面是举例子环节：

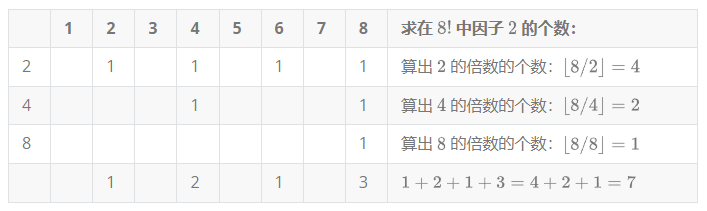
比如求 \(8!\) 中 \(2\) 的个数：

\(4+2+1=7\)，所以一共 \(7\) 个 \(2\) 出现了。

于是我们得到：\(\alpha_i=\left\lfloor\dfrac n{p_i^1}\right\rfloor+\left\lfloor\dfrac n{p_i^2}\right\rfloor+\left\lfloor\dfrac n{p_i^3}\right\rfloor+\dots\)

直到 \(p_i\) 的幂大于 \(n\) 停止循环。

到这里我们可以发现：我们平时求的方法是一列一列求的（就是每一个数算一遍），而这个方法我们一行一行地求，虽然效果一样，但求起来速度很快。值得学习。

写成代码就是：

get_pri(); //线性筛n以内的素数
ll ans = 1; //(n!)^2的因子个数
int tmp = n; //存一下n
for (int i = 1; i <= cnt && pri[i] <= n; i++) {
    int nw = 0; //相当于alpha_i
    while (n) {
        nw += n / pri[i];
        n /= pri[i];
    }
    //注意求的是n!的平方的因子个数，所以alpha_i需要*2之后再+1
    ans = ans * (nw << 1 | 1);
}

上面代码中的 ans 即为答案。

注意

  • 多组数据；
  • 不写高精度只有 10pts。。。高精度模板：OI Wiki。

总结

  1. 大力推式子得到答案为 \((n!)^2\) 的约数个数；
  2. 快速求出 \(n!\) 的每个质因子的次数，由此求出 \((n!)^2\) 的约数个数；
  3. 高精度。

代码

（高精度模板和线性筛模板省略）

#include <iostream>
#include <cstdio>
#include <cstring>
#include <bitset>
#define f(x, y, z) for (register int x = (y); (x) <= (z); (x)++)
#define g(x, y, z) for (register int x = (y); (x) >= (z); (x)--)
using namespace std;
int const N = 10010;

int pri[1600], cnt;
bitset<N> ck;
void get_pri() { ... }

#define MAXN 9999
#define MAXSIZE 10024
struct Big {
	int a[MAXSIZE], len;
	bool flag;  // 标记符号'-'
	Big() {
		len = 1;
		memset(a, 0, sizeof a);
		flag = 0;
	}
	Big(const int);
	Big& operator=(const Big&);
	Big operator*(const Big&) const;
};
Big::Big(const int b) { ... }
Big& Big::operator=(const Big& T) { ... }
Big Big::operator*(const Big& T) const { ... }
inline void print(const Big& s) { ... }

signed main() {
	int n;
	get_pri();
	while (cin >> n, n) {
		Big ans(1);
		for (int i = 1; i <= cnt && pri[i] <= n; i++) {
			int tmp = n, nw = 0;
			while (tmp) {
				nw += tmp / pri[i];
				tmp /= pri[i];
			}
			ans = ans * (nw << 1 | 1);
		}
		print(ans);
	}
	return 0;
}

参考资料

posted @ 2022-11-06 20:08  f2021ljh  阅读(63)  评论(0)    收藏  举报