11.6 L5-NOIP模拟2 B. 牛牛的旅行 题解
L5-NOIP模拟2 B. 牛牛的旅行 题解
标签:树上问题,并查集,排序
题意
给定一棵树,树上有 \(n\) 个节点,节点 \(i\) 的权值为 \(val_i\),两个点 \(u,v\) 间的距离 \(dis(u,v)\) 定义为两点间最短路径包含的边数。
有序点对 \((u,v)(u\ne v)\) 的 happy 值 \(happy(u,v)\) 定义为:路径 \(u\leadsto v\) 上的节点(包括端点)权值中的最大值减去 \(u,v\) 间的距离,即 \(happy(u,v)=\max\limits_{i\in u\leadsto v}\{val_i\}-dis(u,v)\)。
求 \(\sum\limits_{s\ne t}happy(s,t)\bmod(10^9+7)\)。
对于前 \(30\%\) 的测试数据,保证 \(n\le1000\)。
对于另 \(10\%\) 的测试数据,保证给出的树结构退化为一条单链。
对于另 \(10\%\) 的测试数据,保证所有点的 \(val_i\) 都相同。
对于 \(100\%\) 的测试数据,保证 \(2\le n\le10^6,1\le u,v\le n,0\le val_i<10^9 + 7\)。
思路
前 30 pts
暴力枚举端点,跑 lca,时间复杂度 \(O(n^2\log n)\)。
单链 10 pts
相当于在数组上解决这个问题。
对数组进行分治,每次查询区间最大值以及它所在的下标,那么这个区间内所有跨过最大值的子区间的数量就是这个最大值的贡献。可以用乘法原理来算。
然后把数组从最大值处分成左右两部分,继续进行上述操作。
查询区间最大值及其下标的操作可以用线段树维护。
所有 val 值相同 10 pts
观察到 \(\sum happy(s,t)=\sum\max\limits_{i\in s\leadsto t}\{val_i\}-\sum dis(s,t)\),于是我们可以分开计算。
对于前一部分,由于所有 \(val_i\) 均相同,实际上这一部分答案就是路径的个数即 \(n(n-1)\) 乘上 \(val_i\)。
对于后一部分,对于一条边 \((u,v)\),经过它的路径的端点一定是一个在 \(u\) 一侧, 一个在 \(v\) 一侧,所以根据乘法原理,\(u\) 一侧的端点个数乘上 \(v\) 一侧的端点个数即为 \((u,v)\) 对答案的贡献。具体来说,选定任意一个节点为根,DFS 处理出以 \(i\) 为根的子树大小 \(siz_i\),如果 \(v\) 是 \(u\) 的儿子,那么 \((u,v)\) 对答案的贡献即为 \(siz_v\times(n-siz_v)\)。(别忘了是减去不是加上)
100 pts
受到上面 subtask 的启发,我们把答案拆成两部分。
对于后一部分,和上面求解的方法一致。
对于前一部分,我们考虑每一个 \(val_i\) 的贡献。
对于节点 \(i\),以 \(i\) 为中心扩散出一个“影响域”,域内所有点的点权均不大于当前节点 \(i\) 的点权。那么以 \(val_i\) 为最大点权的路径一定在这个影响域范围内。
下图所示为以点权为 \(10\) 的点为中心的影响域。
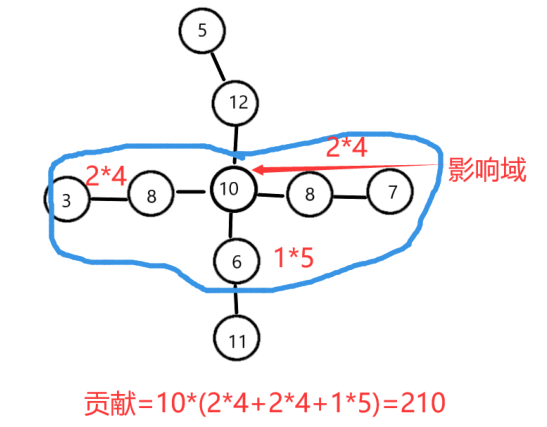
于是就可以计算出 \(val_i\) 的贡献。
把 \(i\) 的影响域看成以 \(i\) 为根的一棵树,设 \(sz_x\) 表示以 \(x\) 为根的子树大小。
如果 \(j\) 是 \(i\) 的儿子,那么贡献为 \(\sum_jval_i\times(sz_i-sz_j)\times sz_j\)。
那么如何维护这个影响域呢?
我们发现小的不可以影响大的,而大的可以影响小的,所以我们将节点按 \(val\) 值从小到大排序,不断扩张影响域。
具体来说,假如当前节点为 \(x\),如果 \(x,y\) 间有连边且节点 \(y\) 已经在另一个影响域内,那么说明 \(y\) 所在影响域内的所有节点权值都不大于 \(x\) 的权值(因为是之前更新的),于是把两个影响域合并。上面所说的 \(x\) 的影响域内以 \(y\) 为根的子树大小即为未合并前的 \(y\) 所在影响域的大小。可以用并查集实现。
代码
注意:答案最后要乘以 2,因为 \((s,t)\) 和 \((t,s)\) 是两个不同的路径。
#include <cstdio>
#include <cctype>
#include <algorithm>
#include <numeric>
#define f(x, y, z) for (int x = (y); (x) <= (z); ++(x))
#define il inline
#define int ll
#define FILENAME "b"
using namespace std;
typedef long long ll;
const int N = 1e6 + 10;
const int MOD = 1e9 + 7;
int n, val[N], ans, a[N];
// Fast_IO by lym
char pri_f[25];void read(){}void print(){putchar(' ');}template<typename T,typename... T2>inline void read(T &x,T2 &... oth){x=0;char ch=getchar();bool f=0;for(;!isdigit(ch);ch=getchar()){if(ch=='-'){f=1;}}for(;isdigit(ch);ch=getchar()){x=(x<<1)+(x<<3)+(ch^48);}if(f){x=(~x+1);}read(oth...);}template<typename T,typename... T2>inline void print(T x,T2 ... oth){int p3=-1;if(x<0){putchar('-');x=(~x+1);}do{pri_f[++p3]=(x%10)|48;}while(x/=10);while(p3>=0){putchar(pri_f[p3--]);}print(oth...);}
struct Edge {
int to, nxt;
} e[N << 1];
int head[N], cnt;
il void add(int from, int to) {
e[++cnt].to = to, e[cnt].nxt = head[from], head[from] = cnt;
return;
}
int siz[N];
void dfs(int u, int fa) {
siz[u] = 1;
for (int i = head[u]; i; i = e[i].nxt) {
int v = e[i].to;
if (v == fa) continue;
dfs(v, u);
siz[u] += siz[v];
}
ans += MOD - (n - siz[u]) * siz[u] % MOD, ans %= MOD;
return;
}
int fa[N], sz[N];
bool in[N];
int getfa(int x) { return x == fa[x] ? x : fa[x] = getfa(fa[x]); }
signed main() {
freopen(FILENAME".in", "r", stdin);
freopen(FILENAME".out", "w", stdout);
read(n);
f(i, 1, n) read(val[i]);
f(i, 1, n - 1) {
int u, v;
read(u, v);
add(u, v), add(v, u);
}
dfs(1, 0);
iota(a + 1, a + n + 1, 1);
sort(a + 1, a + n + 1, [](int const &p, int const &q) { return val[p] < val[q]; });
f(i, 1, n) fa[i] = i, sz[i] = 1;
f(ii, 1, n) {
int i = a[ii];
for (int k = head[i]; k; k = e[k].nxt) {
int j = e[k].to;
if (in[j]) {
int fi = getfa(i), fj = getfa(j);
ans += val[i] * sz[fj] % MOD * sz[fi] % MOD;
ans %= MOD;
if (fi != fj) {
sz[fj] += sz[fi];
fa[fi] = fj;
}
}
}
in[i] = true;
}
print(ans * 2 % MOD);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号