题解 CF1100C 【NN and the Optical Illusion】

本题是道纯数学题，代码很简单。

示意图:

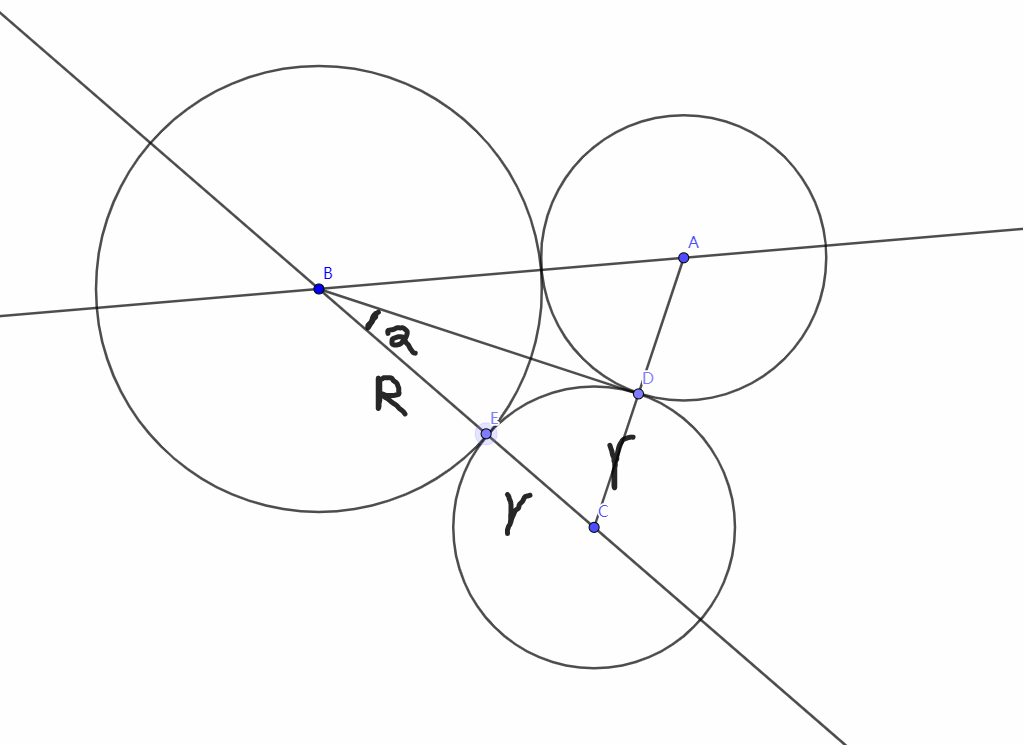
如图所示：

线段 \(BD\) 与 \(\bigcirc A \bigcirc C\) 相切，设 \(R\) 为大圆的半径，\(r\) 为小圆的半径，\(n\) 为小圆个数，则 \(\angle \alpha = (360 \div n \div 2)^\circ\) ，转化为弧度制即为：

\[\pi \cdot 2 \div n \div 2=\frac{\pi}{n} \]

由此则可在 \(Rt\vartriangle BDC\) 设出 \(k=\sin \angle \alpha\)，即可得出方程:

\[r=(r+R)\cdot k \]

化简：

\[r=r \cdot k+R \cdot k \]

\[r-r \cdot k=R \cdot k \]

\[r(1-k)=R \cdot k \]

即

\[r=\frac{R \cdot k}{1-k} \]

代码：

#include<bits/stdc++.h>
using namespace std;
int main()
{
	double n,r;
	double pi=3.14159265358979323846;
	cin>>n>>r;
	double k=sinf(pi/n);
	printf("%.7lf",r*k/(1-k));
}

轻松解决~~