[拉格朗日反演][FFT][NTT][多项式大全]详解

1、多项式的两种表示法

1.系数表示法

我们最常用的多项式表示法就是系数表示法，一个次数界为\(n\)的多项式\(S(x)\)可以用一个向量\(s=(s_0,s_1,s_2,\cdots,s_n-1)\)系数表示如下：

\[S(x)=\sum_{k=0}^{n-1}s_kx^k \]

系数表示法很适合做加法，可以在\(O(n)\)的时间复杂度内完成，表达式为：

\[S(x)=A(x)+B(x)=\sum_{k=0}^{n-1}(a_k+b_k)x^k \]

当中

\[s_k=a_k+b_k \]

但是，系数表示法不适合做乘法，时间复杂度为\(O(n^2)\)，表达式为：

\[S(x)=A(x)B(x)=\sum_{k=0}^{n-1}\left(\sum_{j=0}^{n-1}a_j b_{k-j}\right)x^k \]

当中

\[s_k=\sum_{j=0}^k a_j b_{k-j} \]

这就是卷积的一般形式，记\(s=a\otimes b\)，我们要想办法加速这个过程。

2.点值表示法

顾名思义，点值就是多项式在一个点处的值。多项式\(A(x)\)的点值表达是一个集合：

\[\{(x_0,y_0),(x_1,y_1),(x_2,y_2),\cdots,(x_{n-1},y_{n-1})\} \]

使得对于\(k=0,1,2,\cdots,n-1\)有\(x_k\)两两不相同且\(y_k=A(x_k)\)。

\(n\)个点可以确定唯一一个\(n\)次多项式。

点值表达有很多优良的性质，加法和乘法都可以在\(O(n)\)的时间复杂度内完成。

现有\(A(x)\)的点值表达

\[\{(x_0,y_0),(x_1,y_1),(x_2,y_2),\cdots,(x_{n-1},y_{n-1})\} $$和$B(x)$的点值表达 $$\{(x_0,y'_0),(x_1,y'_1),(x_2,y'_2),\cdots,(x_{n-1},y'_{n-1})\} \]

则\(C(x)=A(x)+B(x)\)的点值表达为：

\[\{(x_0,y_0+y'_0),(x_1,y_1+y'_1),(x_2,y_2+y'_2),\cdots,(x_{n-1},y_{n-1}+y'_{n-1})\} \]

\(C(x)=A(x)B(x)\)的点值表达为：

\[\{(x_0,y_0 y'_0),(x_1,y_1 y'_1),(x_2,y_2 y'_2),\cdots,(x_{n-1},y_{n-1} y'_{n-1})\} \]

可见，点值表示可以帮助我们更快地进行卷积，可是如何在系数表示法和点值表示法之间相互转化呢？

2、复数

当\(x\)为实数时，无法很好地对转换方法进行优化。为了优化计算\(x^n\)所浪费的时间，我们需要\(x\)有循环的性质。但点值表示法需要\(n\)个两两不同的值，而在实数域中只有\(1\)和\(-1\)，因此，我们需要复数的帮助。

1.复数、复平面的定义

我们把形如\(a+bi\)的数称为复数\(z\)，其中\(a\)为实部(Real)，记为\(\Re z\)；\(b\)为虚部(Imaginary)，记为\(\Im z\)。

每一点都对应唯一复数的平面叫复平面，相当于一个把\(\Re z\)作为横坐标，把\(\Im z\)作为纵坐标的笛卡尔坐标系。如图：

模长：复平面上原点到复数\(z\)的距离，记为\(|z|\)。根据勾股定理，\(|z|=|a+bi|=\sqrt{a^2+b^2}\)

辐角：复平面上\(x\)轴与复数\(z\)所对应向量之间的夹角，在\((-\frac{\pi}{2},\frac{\pi}{2})\)之间的记为辐角主值\(\arg z\)。

2.欧拉公式

大名鼎鼎的欧拉公式：

\[e^{i t}=\cos t+i\sin t \]

根据三角函数在单位圆上的几何意义，公式是容易理解的。

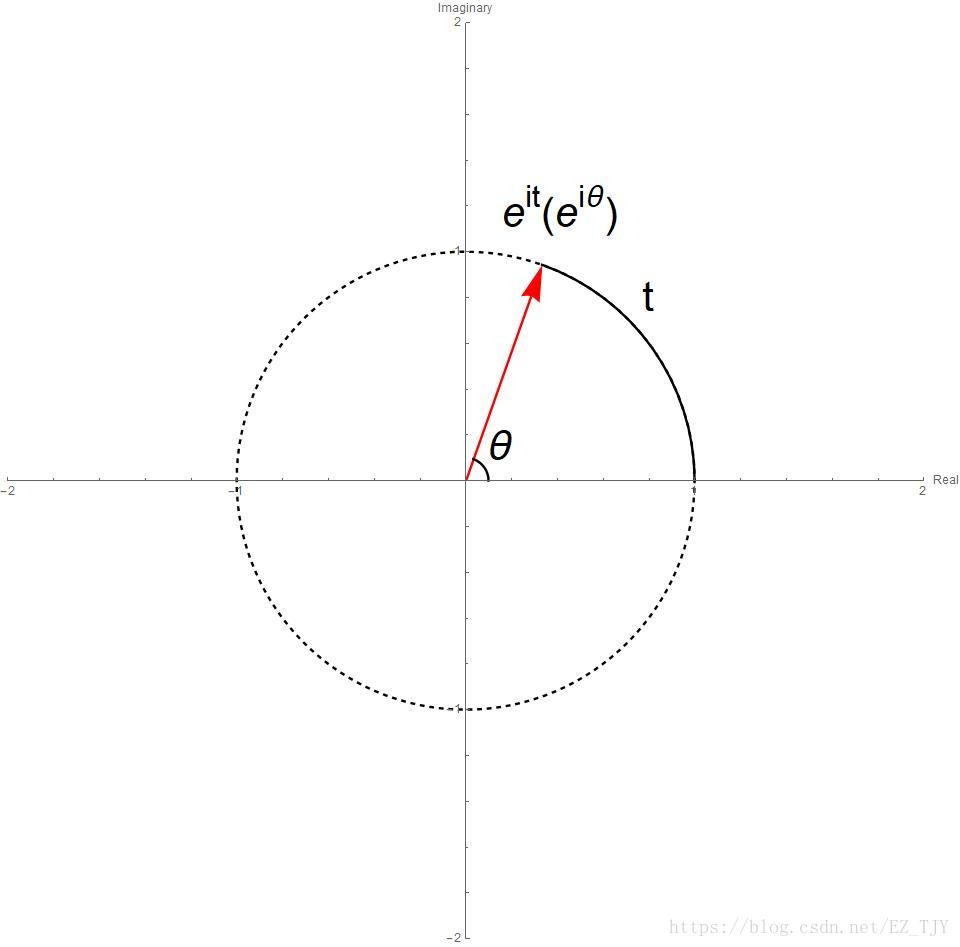
几何意义：

当中\(\theta\)为角度，\(t\)为弧长。

证明：

对\(\exp(x)\)在\(x=0\)泰勒展开：

\[\exp(x)=\sum_{k=0}^\infty\frac{x^k}{k!} \]

对\(\sin(x)\)在\(x=0\)泰勒展开：

\[\sin(x)=\sum_{k=0}^\infty\frac{x^{4 k+1}}{(4 k+1)!}-\sum_{k=0}^\infty\frac{x^{4 k+3}}{(4 k+3)!} \]

对\(\cos(x)\)在\(x=0\)泰勒展开：

\[\cos(x)=\sum_{k=0}^\infty\frac{x^{4 k}}{(4 k)!}-\sum_{k=0}^\infty\frac{x^{4 k+2}}{(4 k+2)!} \]

把\(\exp(x)\)中的\(x\)替换为\(i x\)：

\[\exp(i x)=\sum_{k=0}^\infty\frac{x^{4 k}}{(4 k)!}+i\sum_{k=0}^\infty\frac{x^{4 k+1}}{(4 k+1)!}-\sum_{k=0}^\infty\frac{x^{4 k+2}}{(4 k+2)!}-i\sum_{k=0}^\infty\frac{x^{4 k+3}}{(4 k+3)!} \]

则显然有：

\[e^{i x}=\cos x+i\sin x \]

证毕。

则根据欧拉公式，可将一个复数表示为一个二元组\((a,\theta)\)，即模长和辐角（相当于复平面上极坐标系的表示方法）。值为:\(a(\cos\theta+i\sin\theta)\)

特殊情况：欧拉恒等式\(e^{i\pi}+1=0\)

3.复数的运算

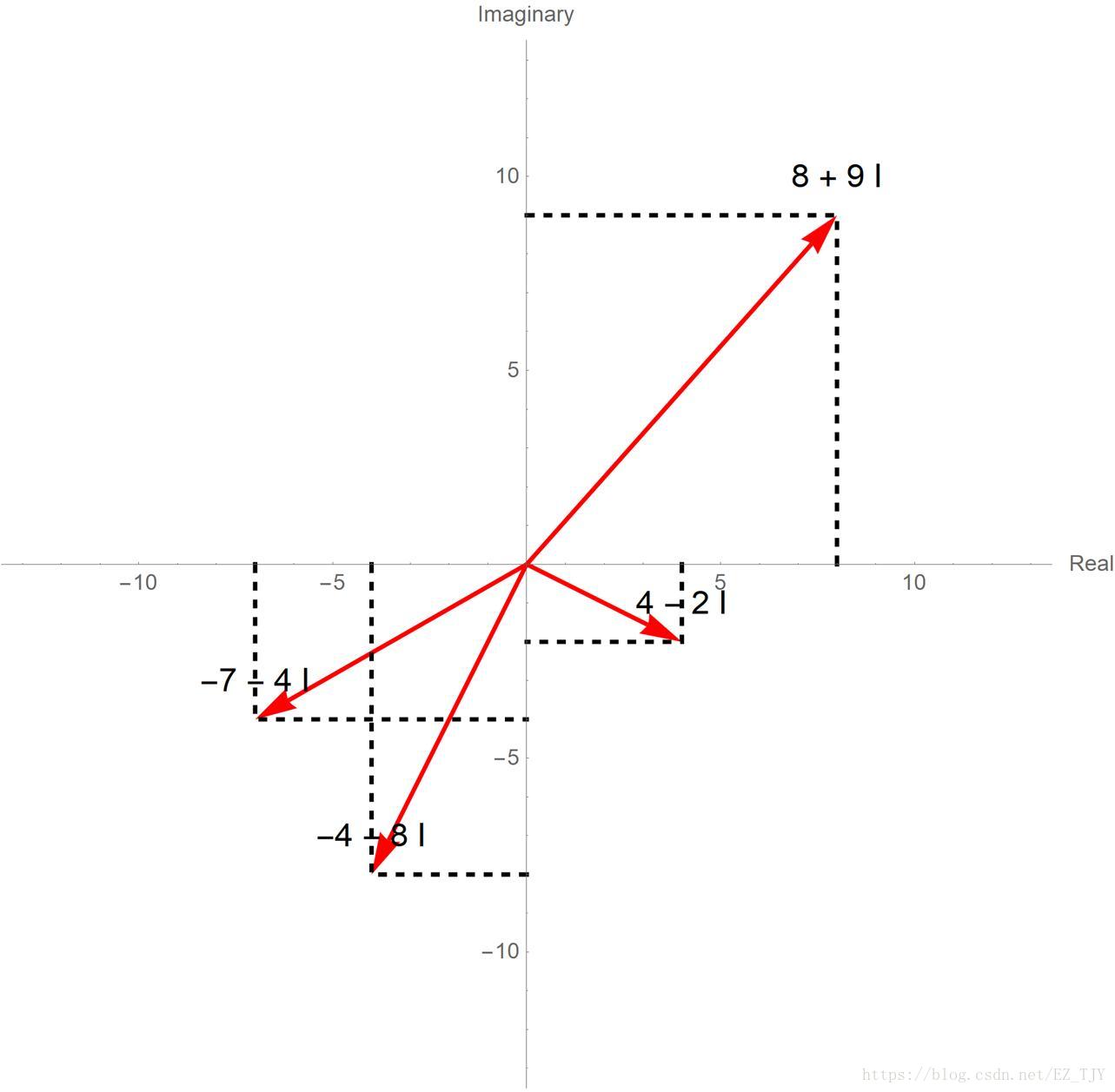
（1）复数加法

运算规则：实部、虚部分别相加

\[(a+bi)+(c+di)=a+c+bi+di=(a+c)+(b+d)i \]

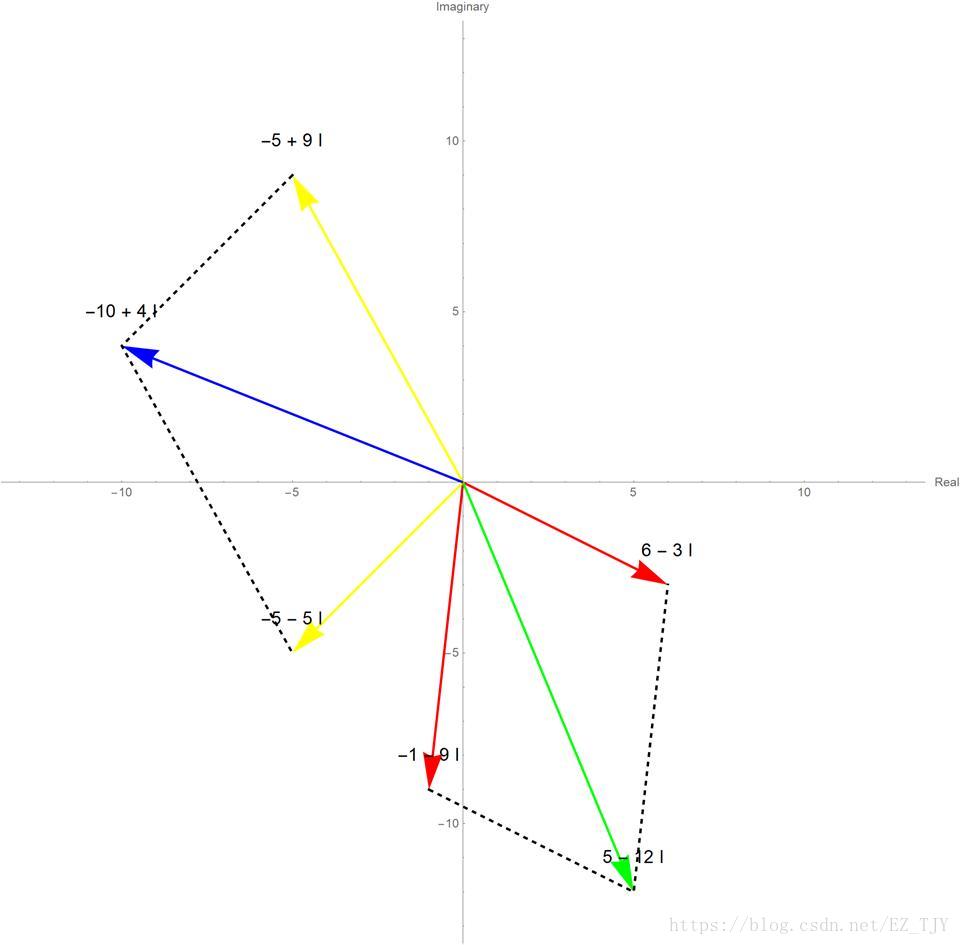
几何意义：如图

结果相当于两个向量所构成的平行四边形的对角线。如果把一个复数所对应的向量视为一个移动的变换，那么向量加法就是连续运用这两个变换相当于的新变换。

（2）复数乘法

运算规则：展开

\[(a+bi)(c+di)=ac+adi+bci+bdi^2=(ac-bd)+(ad+bc)i \]

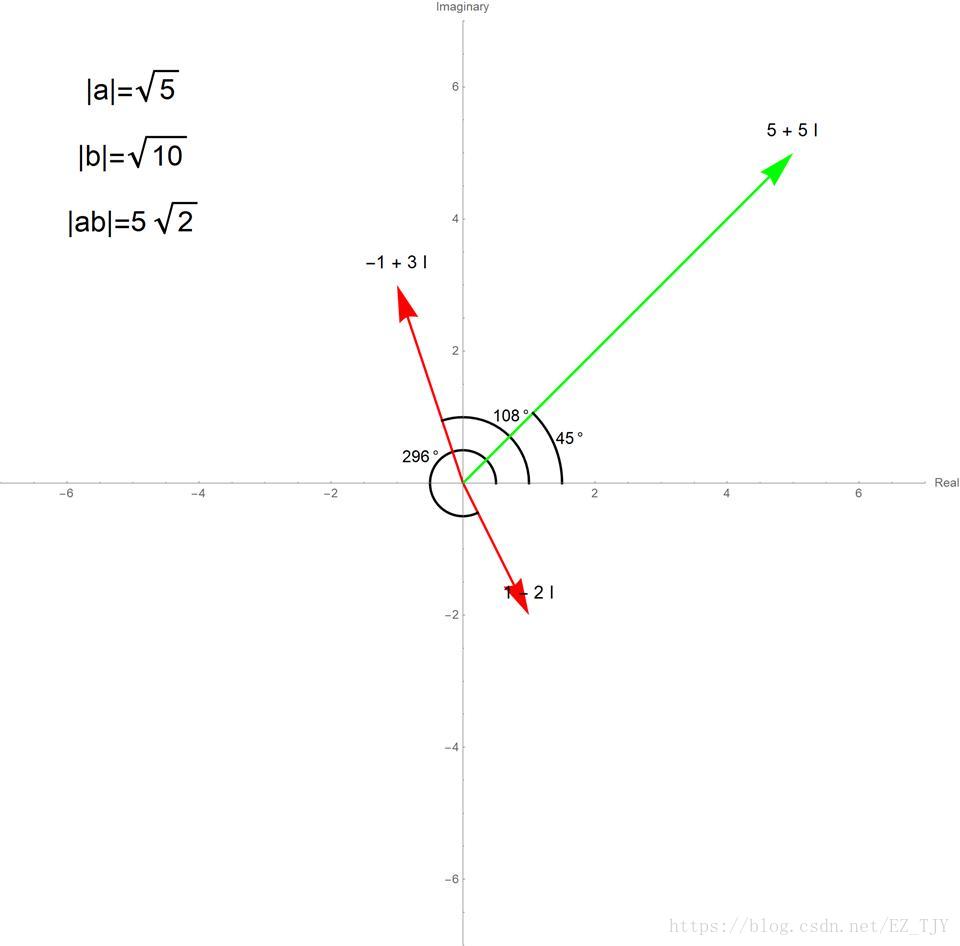
几何意义：如图

如图，\(\arg a+\arg b=\arg a\times b\),\(|a|\times|b|=|a\times b|\)

总结就是：模长相乘，辐角相加。

因此，如果模长为\(1\)，那么它的\(n\)次方一定还在单位圆上。

证明：

根据欧拉公式，已知\(x=(a_1,\theta_1)=a_1(\cos\theta_1+i\sin\theta_1),y=(a_2,\theta_2)=a_2(\cos\theta_2+i\sin\theta_2)\)

则

\[\begin{align*} x\times y&=a_1 a_2(\cos\theta_1+i\sin\theta_1)(\cos\theta_2+i\sin\theta_2)\\ &=a_1 a_2\left[(\cos\theta_1\cos\theta_2-\sin\theta_1\sin\theta_2)+i(\cos\theta_1\sin\theta_2+\sin\theta_1\cos\theta_2)\right]\\ &=a_1 a_2\left[\cos(\theta_1+\theta_2)+i\sin(\theta_1+\theta_2)\right]\tag{和角公式}\\ \end{align*} \]

\(\therefore |x\times y|=|x|\times |y|,\arg(x\times y)=\arg x+\arg y\)

证毕。

4.单位复数根

（1）基本性质

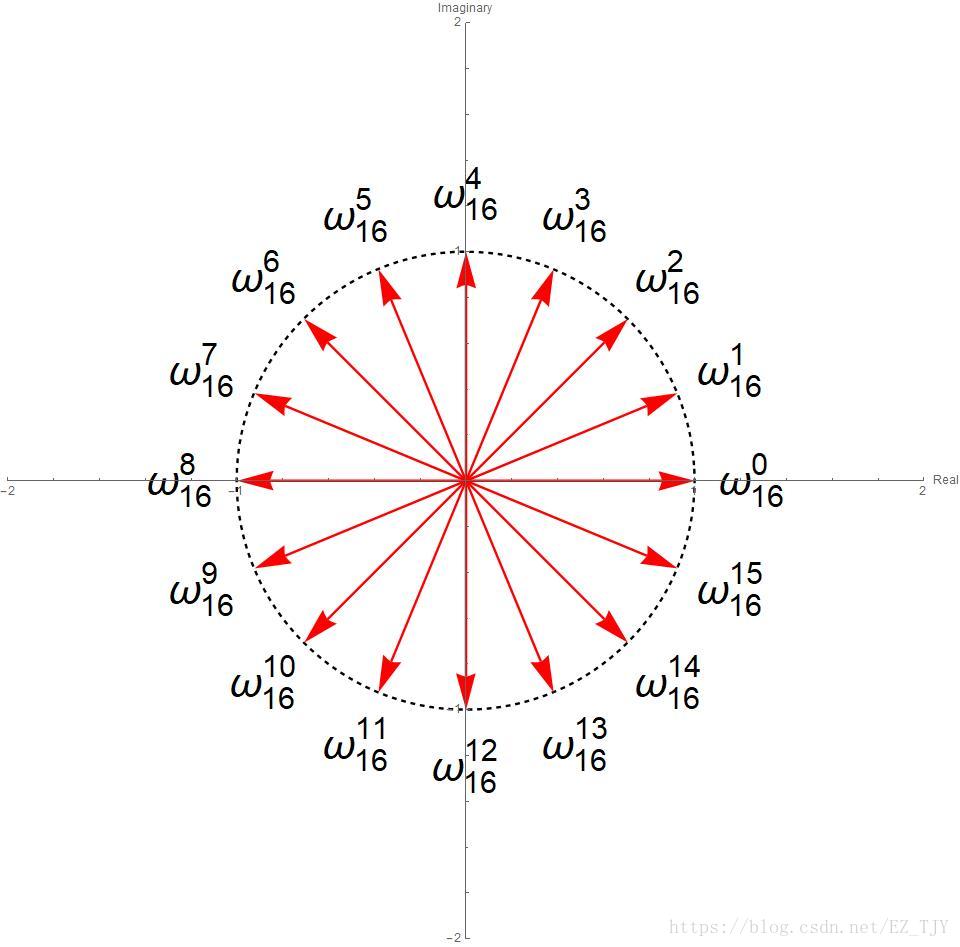
单位复数根是方程\(\omega^n=1\)的解，第\(k\)个解记为\(\omega_n^k\)(这里的\(k\)事实上是乘方的含义)

\(n=16\)的解在复平面上的位置如下：

可以看到，\(n\)个解把单位圆分成了\(n\)等弧，交点即为根。而且，\(\omega_n^k\)实际上是\(\omega_n\)的\(n\)次方，模长仍为\(1\),辐角翻倍！

为什么呢？

\(\because |x^n|=|x|^n,\arg x^n=n\arg x\)

\(\therefore |\omega|^n=|\omega^n|,\arg\omega^n=n\arg\omega\)

\(\therefore |\omega|^n=1(|\omega|\in\mathbb{R}^+),\arg\omega=\frac{360^\circ}{n}\)

\(\therefore |\omega|=1,\arg\omega=\frac{360^\circ}{n}\)

这就很明显了。

所以，\(\omega_n^k\)事实上表示的是\(\omega_n\)的\(k\)次幂。为什么选择单位复数根呢？因为它有循环的优良性质，即\(\omega_n^n=1\)。由于其他的都可以由\(\omega_n^1\)得到，因此称为主\(n\)次单位根，又记为\(\omega_n\)。

根据单位复数根的平分圆的意义和欧拉公式，\(\omega_n^k=e^\frac{2\pi i k}{n}=\cos\frac{2\pi k}{n}+i\sin\frac{2\pi k}{n}\)。

（2）计算引理

显然，由于单位复数根循环(\(\omega_n^{zn}=e^{2\pi iz}=\left[\left(e^{\pi i}\right)^2\right]^z=1^z=1\))，有变换恒等式：

\[\omega_n^k=\omega_n^{k+wn}(w\in\mathbb{Z}) \]

每一份再分成\(k\)份，编号也变成\(k\)倍，位置自然不变(\(\omega_{d n}^{d k}=e^\frac{2\pi i d k}{dn}=e^\frac{2\pi i k}{n}=\omega_n^k\))，所以有消去引理：

\[\omega_{d n}^{d k}=\omega_n^k \]

由于过了\(n/2\)就会绕过半圈(\(\omega_n^{n/2}=e^\frac{\pi i n}{n}=e^{\pi i}=-1\))，所以有折半引理：

\[\omega_n^k=-\omega_n^{k\pm n/2} \]

对单位复数根求和，根据几何级数(等差数列求和公式)，可得(\(\sum\limits_{k=0}^{n-1}(\omega_n^k)^j=\frac{(\omega_n^n)^j-1}{\omega_n^1-1}=0\))，即有求和引理（要注意公式的使用条件）：

\[\sum_{k=0}^{n-1}(\omega_n^k)^j=0,\omega_n\ne 1 \]

3、DFT&FFT

1.DFT

DFT就是求多项式\(A(x)\)在点\((\omega_n^0,\omega_n^1,\omega_n^2,\cdots,\omega_n^{n-1})\)处取值的过程。即：

\[y_k=A(\omega_n^k)=\sum_{j=0}^{n-1}a_j\omega_n^{kj} \]

结果\(y=(y_0,y_1,y_2,\cdots,y_{n-1})\)就是\(a\)的离散傅里叶变换(DFT),记为\(y=DFT_n(a)\)

2.FFT

（1）递归

DFT的\(O(n^2)\)算法太慢了，FFT使用分治策略优化速度到\(O(n\log n)\)。

考虑奇偶分治。

现在，我们假设\(n=2^t\)，设原系数\(a=(a_0,a_1,a_2,\cdots,a_{n-1})\)，分治为偶数部分\(a_1=(a_0,a_2,a_4,\cdots,a_{n-2})\)，奇数部分\(a_2=(a_1,a_3,a_5,\cdots,a_{n-1})\)，已经递归求出\(y_1=DFT_{n/2}(a_1)\)，\(y_2=DFT_{n/2}(a_2)\)，现在我们要合并\(y_1,y_2\)，得到\(y=DFT_n(a)\)(蝴蝶操作)。
\begin{align}
对于\(n=1\)的边界情况，结果是显然的：因为\(k=0\)，故\(\omega_1^0=1\)，即结果等于原系数。

对于\(n>1\)，现在我们枚举\(k\in[1,n]\)要合并出\(y_k\)：

\[\begin{align*} y_k&=A(\omega_n^k)\\ &=\sum_{j=0}^{n-1}a_j\omega_n^{kj}\\ &=\sum_{j=0}^{n/2-1}a_{2 j}\omega_n^{2 k j}+\sum_{j=0}^{n/2-1}a_{2 j+1}\omega_n^{2 k j+k}\\ &=\sum_{j=0}^{n/2-1}a_{2 j}\omega_n^{2 k j}+\omega_n^k\sum_{j=0}^{n/2-1}a_{2 j+1}\omega_n^{2 k j}\\ &=\sum_{j=0}^{n/2-1}a_{1_j}\omega_{n/2}^{k j}+\omega_n^k\sum_{j=0}^{n/2-1}a_{2_j}\omega_{n/2}^{k j}\tag{消去引理} \end{align*} \]

• 对于\(k<n/2\)：

\[\begin{align*} y_k&=y_{1_k}+\omega_n^k y_{2_k} \end{align*} \]

• 对于\(k\geq n/2\)：

\[\begin{align*} y_k&=\sum_{j=0}^{n/2-1}a_{1_j}\omega_{n/2}^{(k-n/2)j}+\omega_n^k\sum_{j=0}^{n/2-1}a_{2_j}\omega_{n/2}^{(k-n/2)j}\tag{变换恒等式}\\ &=y_{1_{k-n/2}}+\omega_n^k y_{2_{k-n/2}}\\ &=y_{1_{k-n/2}}-\omega_n^{k-n/2}y_{2_{k-n/2}}\tag{折半引理} \end{align*} \]

我们用\(k+n/2\)替代\(k\)，就得到\(y_{k+n/2}=y_{1_k}-\omega_n^k y_{2_k}\)

结合在一起就得到\(\begin{cases}y_k&=y_{1_k}+\omega_n^k y_{2_k}\\y_{k+n/2}&=y_{1_k}-\omega_n^k y_{2_k}\end{cases}\)
这样我们就可以把两个\(n/2\)长的序列合并为一个\(n\)长的序列了。

以下图的递归序，就可以在\(O(n\log n)\)的时间复杂度内完成求解了。

（2）迭代

递归方法消耗内存、时间过大，无法承受。我们每次把下标分为奇数部分和偶数部分，是否有办法直接求出最后的递归运算顺序，以避免递归呢？

这样想：
第一次奇偶划分，我们按照二进制的倒数第一位排序；
第二次奇偶划分，我们按照二进制的倒数第二位排序；
第\(n\)次奇偶划分，我们按照二进制的倒数第\(n\)位排序；
依此类推。

因此，结果顺序就是原序列按照二进制位翻转的大小排序的结果。只要依次交换\(a_k,a_{rev(k)}\)，求出序列，就可以用迭代方法相邻归并实现快速傅里叶变换。

或者，我们也可以用更加代数的方法来发现这个结论。
已知现在位置为\(k=(b_1 b_2 b_3 \cdots b_n)_2\)，按照奇偶重排：

• 若\(b_n=0\)，则位置变为\(\frac{k}{2}=(0 b_1 b_2 \cdots b_{n-1})_2=(b_n b_1 b_2 \cdots b_{n-1})_2\)，即为把最后一位提到第一位。
• 若\(b_n=1\)，则位置变为\(2^{n-1}-1+\frac{k+1}{2}=\frac{2^n+k-1}{2}=\frac{(1 b_1 b_2 \cdots b_{n-1} 0)_2}{2}=(b_n b_1 b_2 \cdots b_{n-1})_2\)，同样是把最后一位提到第一位。

则反复\(n\)次之后，就相当于二进制反转了。

如\(n=8\)时，求出二进制：

0	1	2	3	4	5	6	7
\(000_2\)	\(001_2\)	\(010_2\)	\(011_2\)	\(100_2\)	\(101_2\)	\(110_2\)	\(111_2\)

翻转：

0	1	2	3	4	5	6	7
\(000_2\)	\(100_2\)	\(010_2\)	\(110_2\)	\(001_2\)	\(101_2\)	\(011_2\)	\(111_2\)

按翻转后的值排序：

0	4	2	6	1	5	3	7
\(000_2\)	\(001_2\)	\(010_2\)	\(011_2\)	\(100_2\)	\(101_2\)	\(110_2\)	\(111_2\)

这样就可以把奇偶合并转化为左右归并，迭代实现了。

5、IDFT&IFFT

何把点值表达变回系数表达呢？如果把求值写成矩阵形式，就是：

\[\begin{bmatrix} \omega_n^0 & \omega_n^0 & \omega_n^0 & \omega_n^0 & \cdots & \omega_n^0 \\ \omega_n^0 & \omega_n^1 & \omega_n^2 & \omega_n^3 & \cdots & \omega_n^{n-1} \\ \omega_n^0 & \omega_n^2 & \omega_n^4 & \omega_n^6 & \cdots & \omega_n^{2(n-1)} \\ \omega_n^0 & \omega_n^3 & \omega_n^6 & \omega_n^9 & \cdots & \omega_n^{3(n-1)} \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ \omega_n^0 & \omega_n^{n-1} & \omega_n^{2(n-1)} & \omega_n^{3(n-1)} & \cdots & \omega_n^{(n-1)^2} \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_{n-1} \end{bmatrix}= \begin{bmatrix} y_0 \\ y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_{n-1} \end{bmatrix} \]

如果我们要把\(y\)变成\(a\)，就需要求出第一个矩阵的逆，即：

\[\begin{bmatrix} a_0 \\ a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_{n-1} \end{bmatrix}= \begin{bmatrix} \omega_n^0 & \omega_n^0 & \omega_n^0 & \omega_n^0 & \cdots & \omega_n^0 \\ \omega_n^0 & \omega_n^1 & \omega_n^2 & \omega_n^3 & \cdots & \omega_n^{n-1} \\ \omega_n^0 & \omega_n^2 & \omega_n^4 & \omega_n^6 & \cdots & \omega_n^{2(n-1)} \\ \omega_n^0 & \omega_n^3 & \omega_n^6 & \omega_n^9 & \cdots & \omega_n^{3(n-1)} \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ \omega_n^0 & \omega_n^{n-1} & \omega_n^{2(n-1)} & \omega_n^{3(n-1)} & \cdots & \omega_n^{(n-1)^2} \end{bmatrix}^{-1} \begin{bmatrix} y_0 \\ y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_{n-1} \end{bmatrix} \]

这个范德蒙德矩阵极为特殊，它的逆矩阵是：

\[\begin{bmatrix} a_0 \\ a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_{n-1} \end{bmatrix}=\frac{1}{n} \begin{bmatrix} \omega_n^0 & \omega_n^0 & \omega_n^0 & \omega_n^0 & \cdots & \omega_n^0 \\ \omega_n^0 & \omega_n^{-1} & \omega_n^{-2} & \omega_n^{-3} & \cdots & \omega_n^{-(n-1)} \\ \omega_n^0 & \omega_n^{-2} & \omega_n^{-4} & \omega_n^{-6} & \cdots & \omega_n^{-2(n-1)} \\ \omega_n^0 & \omega_n^{-3} & \omega_n^{-6} & \omega_n^{-9} & \cdots & \omega_n^{-3(n-1)} \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ \omega_n^0 & \omega_n^{-(n-1)} & \omega_n^{-2(n-1)} & \omega_n^{-3(n-1)} & \cdots & \omega_n^{-(n-1)^2} \end{bmatrix} \begin{bmatrix} y_0 \\ y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_{n-1} \end{bmatrix} \]

只是把每项取倒数，并将结果除以\(n\)即可。

证明：

记原矩阵为\(A_{n n}\),我们给出的矩阵为\(B_{n n}\)。

\(\therefore A_{i j}=\omega_n^{i j},B_{i j}=\frac{1}{n}\omega_n^{-i j}(0\le i,j\le n-1)\)

\[\begin{align*} AB_{i j}&=\sum_{k=0}^{n-1} A_{i k}B_{k j}\\ &=\frac{1}{n}\sum_{k=0}^{n-1} \omega_n^{i k}\omega_n^{-k j}\\ &=\frac{1}{n}\sum_{k=0}^{n-1} \omega_n^{i k-k j}\\ &=\frac{1}{n}\sum_{k=0}^{n-1} (\omega_n^{i-j})^k \end{align*} \]

• 当\(i=j\)时：

\[\begin{align*} AB_{i j}&=\frac{1}{n}\sum_{k=0}^{n-1}1^k\\ &=\frac{1}{n}\times n\\ &=1 \end{align*} \]

• 当\(i\ne j\)时：

\[\begin{align*} AB_{i j}&=\frac{1}{n}\sum_{k=0}^{n-1}(\omega_n^{i-j})^k\\ &=0\tag{求和引理} \end{align*} \]

综上所述，\(AB=I_n\)，即\(B=A^{-1}\)

以上，离散傅里叶逆变换(IDFT)的表达式为：

\[a_k=\frac{1}{n}\sum_{j=0}^{n-1}y_k\omega_n^{-k j} \]

记\(a=IDFT_n(y)\)。

同理，可以用相同的方法把IDFT加速到\(O(n\log n)\),称为IFFT。

5、NTT

1.定义

有时候我们会想要模素数\(p\)意义下的多项式乘法。此时，由次数界为\(n\)的多项式\(A(x),B(x)\)的系数表达\(a,b\)求\(S(x)=A(x)B(x)\)的系数表达\(s\)的公式为：

\[s_k=\sum_{j=0}^k a_j b_{k-j}\mod p \]

FFT无能为力，我们需要一种新的DFT，以数论的办法进行，这就是快速数论变换(NTT)。

2.原根

（1）定义

我们需要一种有数论循环性质的新数，原根恰好满足我们的要求。

设\(m\)为正整数，\(a\)为整数，若\(a\)模\(m\)的阶等于\(\varphi(m)\)，则称\(a\)为模\(m\)的一个原根。

假设\(g\)是素数\(p\)的原根，有\(1<g<p\)，且对于\(k=0,1,2,\cdots,p-1\)，有\(g^k\mod p\)的结果两两不同，且\(g^{p-1}\equiv 1 \pmod p\)。

可以发现，原根同样有循环的性质。因此，我们类比\(\omega_n^k\)的定义，把原来的\(\omega_n^k=e^\frac{2\pi ik}{n}\)替换为\(g^\frac{k(p-1)}{n}\)。

（2）性质

我们来证明一些类似单位复数根的性质。

变换恒等式：
因为：

\[g^{p-1}\equiv 1 \]

所以：

\[g^\frac{(k+n)(p-1)}{n}\equiv g^\frac{k(p-1)}{n}g^{p-1}\equiv g^\frac{k(p-1)}{n} \]

---

消去引理：
显然有：

\[g^\frac{d k(p-1)}{d n}\equiv g^\frac{k(p-1)}{n} \]

---

折半引理：
因为：

\[g^\frac{(k+\frac{n}{2})(p-1)}{n}\equiv g^\frac{k(p-1)}{n}g^\frac{p-1}{2} \]

所以若要使：

\[g^\frac{k(p-1)}{n}+g^\frac{(k+\frac{n}{2})(p-1)}{n}\equiv 0\pmod p \]

成立，即：

\[g^\frac{k(p-1)}{2}\left(1+g^\frac{p-1}{2}\right)\equiv 0 \]

只需证：

\[g^\frac{p-1}{2}\equiv p-1 \]

由于：

\[g^{k}\equiv 0,1,2,\cdots,p-1 \]

那么我们可以设：

\[g^\frac{p-1}{2}\equiv x,x=0,1,2,\cdots,p-1 \]

因为：

\[\left(g^\frac{p-1}{2}\right)^2\equiv g^{p-1}\equiv 1 \]

所以：

\[x^2-1\equiv 0 \]

即：

\[(x+1)(x-1)\equiv 0 \]

又因为\(p\)为素数，所以有：

\[x+1\equiv 0\;或\;x-1\equiv 0 \]

所以：

\[x=1,p-1 \]

又因为：

\[g^{p-1}\equiv 1,g^k\mod p两两不同 \]

所以：

\[x=p-1 \]

即：

\[g^\frac{p-1}{2}\equiv p-1 \]

得证：

\[g^\frac{k(p-1)}{n}+g^\frac{(k+\frac{n}{2})(p-1)}{n}\equiv 0 \]

---

求和引理：

\[\sum\limits_{k=0}^{n-1}g^\frac{k j(p-1)}{n}\equiv\sum\limits_{k=0}^{n-1}\left(g^\frac{j(p-1)}{n}\right)^k\equiv\frac{g^\frac{n j(p-1)}{n}-1}{g^\frac{j(p-1)}{n}-1}\equiv\frac{\left(g^{p-1}\right)^j-1}{g^\frac{j(p-1)}{n}-1}\equiv 0 \]

这样，我们就证明了原根由于复数单位根相同的性质。

3.公式

我们用原根替换复数单位根，得到：

\[y_k=A(g^\frac{k(p-1)}{n})=\sum_{j=0}^{n-1}a_j g^\frac{k j(p-1)}{n} \]

即\(y=NTT_n(a)\)。逆变换：

\[a_k=\frac{1}{n}\sum_{j=0}^{n-1}y_k g^\frac{-k j(p-1)}{n} \]

即\(a=INTT_n(y)\)。

6、其他扩展

1.任意模数FFT

有的时候我们需要卷积后模上一个数，这个数不是NTT模数，甚至可能不是个质数。那我们该怎么做呢？

这里使用拆系数FFT，本质是以时间换精度。

现在给定次数界为\(m\)的两个多项式\(A(x),B(x)\)，要求\(A(x)B(x) \mod P\)。

首先，令\(M=\lfloor\sqrt{P}\rfloor\)，再对于每个\(a_i\)或\(b_i\)，把其变为\(k_i M+r_i(r_i<M)\)的形式。这样，\(k_i\)和\(r_i\)就都小于等于\(M\)了。

那么卷积就可以写成：

\[c_i=\sum_{k=0}^i a_k b_{i-k}=\sum_{k=0}^i(k_{a_i}M+r_{a_i})(k_{b_{i-k}}M+r_{b_{i-k}})=M^2\sum_{k=0}^i k_{a_i}k_{b_{i-k}}+M\sum_{k=0}^i (k_{a_i}r_{b_{i-k}}+r_{a_i}k_{b_{i-k}})+\sum_{k=0}^i r_{a_i}r_{b_{i-k}} \]

那么我们看到，\(c_i\)可以由\(k\)和\(r\)合并得到。那么我们对\(k_a,k_b,r_a,r_b\)分别做FFT，再对应算出\(x_1=k_a k_b,x_2=k_a r_b+r_a k_b,x_3=r_a r_b\)，对它们再分别做IFFT，就可以由\(c=M^2 x_1+M x_2+x_3\)得到答案了。

这么做的好处究竟在哪里呢？事实上，计算后的最大值由\(m P\)变为了\(m \lfloor\sqrt{P}\rfloor\)，避免了溢出。

P.S. 还有一种基于NTT和中国剩余定理的做法

时间复杂度：\(O(n\log n)\)，常数为\(7\)。

2.多项式求逆

现在我们有一个次数界为\(n\)的多项式\(A(x)\)，要求\(B(x)\)满足\(A(x)B(x)\equiv 1\pmod{x^n}\)。

我们考虑倍增实现。

• 当\(n=1\)时，直接求逆元求得\(B(x)\equiv A(x)^{p-2}\)。
• 当\(n>1\)时，已有\(A(x)G(x)\equiv 1\pmod{x^\frac{n}{2}}\)：

因为：

\[A(x)B(x)\equiv 1\pmod{x^n} \]

又因为除了\(0\)次项之外到\(n-1\)次都为\(0\)，因此到\(\frac{n}{2}-1\)次项也为零：

\[A(x)B(x)\equiv 1\pmod{x^\frac{n}{2}} \]

又

\[A(x)G(x)\equiv 1\pmod{x^\frac{n}{2}} \]

两式相减：

\[A(x)[B(x)-G(x)]\equiv 0\pmod{x^\frac{n}{2}} \]

因为：

\[A(x)\ne 0 \]

所以：

\[B(x)-G(x)\equiv 0\pmod{x^\frac{n}{2}} \]

既然\(0\)至\(\frac{n}{2}-1\)次项都为零，那么平方之后\(0\)至\(n-1\)次项也为零：

\[B(x)^2-2 B(x)G(x)+G(x)^2\equiv 0\pmod{x^n} \]

又

\[A(x)B(x)\equiv 1\pmod{x^n} \]

两边同时乘上\(A(x)\)，得：

\[B(x)-2 G(x)+A(x)G(x)^2\equiv 0\pmod{x^n} \]

移项，得：

\[B(x)\equiv 2 G(x)-A(x)G(x)^2\pmod{x^n} \]

这样就可以了。

时间复杂度证明：

显然有递归式：

\[\begin{cases}T(0)=1\\T(n)=T(\frac{n}{2})+n\log_2(n)\end{cases} \]

展开可得：

\[\begin{align*} T(n)&=\sum_{i=0}^{\log_2(n)}2^i \log_2(2^i)\\ &=\sum_{i=0}^{\log_2(n)}2^i i \end{align*} \]

即我们要求和式：

\[S_n=\sum_{k=0}^n 2^k k \]

的值。

对和式用扰动法，得：

\[\begin{align*} S_n+(n+1)2^{n+1}&=\sum_{k=0}^n (k+1)2^{k+1}\\ S_n+(n+1)2^{n+1}&=2\sum_{k=0}^n k 2^k+2\sum_{k=0}^n 2^k\\ S_n+(n+1)2^{n+1}&=2S_n+2^{n+2}-2\\ -S_n&=2^{n+2}-2-(n+1)2^{n+1}\\ S_n&=2((n+1)2^n-2^{n+1}+1)\\ S_n&=2(2^n n-2^n+1) \end{align*} \]

代入，得：

\[\begin{align*} T(n)&=S_{\log_2(n)}\\ &=2(2^{\log_2(n)}\log_2(n)-2^{\log_2(n)}+1)\\ &=2(n\log_2(n)-n+1)\\ \end{align*} \]

则时间复杂度为：

\[O(T(n))=O(n \log n) \]

因为多项式乘法的常数为\(3\)，因此多项式求逆的常数为\(2\times3=6\)。

3.多项式开根

前置：多项式求逆。

现在我们有一个次数界为\(n\)的多项式\(A(x)\)，要求\(B(x)\)满足\(B(x)^2\equiv A(x)\pmod{x^n}\)。

还是倍增。

• 当\(n=1\)时，\(B(x)\)等于\(A(x)\)在模意义下的开根。
• 当\(n>1\)时，已有\(G(x)^2\equiv A(x)\pmod{x^\frac{n}{2}}\)：

因为：

\[G(x)^2\equiv A(x)\pmod{x^\frac{n}{2}} \]

移项，得：

\[G(x)^2-A(x)\equiv 0\pmod{x^\frac{n}{2}} \]

两边平方，同理可得：

\[G(x)^4-2 G(x)^2 A(x)+A(x)^2\equiv 0\pmod{x^n} \]

所以：

\[[G(x)^2+A(x)]^2-4 G(x)^2 A(x)\equiv 0\pmod{x^n} \]

即：

\[[G(x)^2+A(x)]^2\equiv 4 G(x)^2 A(x)\pmod{x^n} \]

除过去：

\[\frac{[G(x)^2+A(x)]^2}{4 G(x)^2}\equiv A(x)\pmod{x^n} \]

得到：

\[A(x)\equiv\left(\frac{G(x)^2+A(x)}{2 G(x)}\right)^2\equiv B(x)^2\pmod{x^n} \]

即：

\[B(x)\equiv\frac{G(x)^2+A(x)}{2 G(x)}\equiv\frac{A(x)}{2 G(x)}+\frac{G(x)}{2}\pmod{x^n} \]

这就可以了。

时间复杂度：\(O(n\log n)\)，常数为\(2\times(6+3)=18\)。

4.多项式求导

根据导数的可加性和幂函数求导法则\(\frac{\mathbb{d}(cx^k)}{\mathbb{d}x}=c k x^{k-1}\)，有多项式的导数为：

\[\frac{\mathbb{d}(\sum\limits_{k=0}^{n-1}a_k x^k)}{\mathbb{d} x}=\sum_{k=0}^{n-1}\frac{\mathbb{d}(a_k x^k)}{\mathbb{d} x}=\sum_{k=1}^{n-1}k a_k x^{k-1}=\sum_{k=0}^{n-2}(k+1)a_{k+1}x^k \]

时间复杂度：\(O(n)\)，常数为\(1\)。

5.多项式积分

根据积分的可加性和幂函数的不定积分\(\displaystyle\int c x^k\mathbb{d}x=\frac{c}{k}x^{k+1}\)，有多项式的不定积分为：

\[\int\sum_{k=0}^{n-1}a_k x^k \mathbb{d}x=\sum_{k=0}^{n-1}\int a_k x^k\mathbb{d}x=\sum_{k=0}^{n-1}\frac{a_k}{k+1}x^{k+1}=\sum_{k=1}^n\frac{a_{k-1}}{k}x^k \]

时间复杂度：\(O(n)\)，常数为\(1\)。

6.多项式求ln

前置：多项式求导&积分&求逆

现在已知多项式\(A(x)\)，要求\(B(x)=\ln A(x)\)。我们两边微分，得到：

\[B'(x)=\frac{\mathbb{d}(\ln A(x))}{\mathbb{d} A(x)}\frac{\mathbb{d} A(x)}{\mathbb{d} x} \]

\[B'(x)=\frac{A'(x)}{A(x)} \]

再两边积分，就得到：

\[B(x)=\int\frac{A'(x)}{A(x)}\mathbb{d}x \]

因此，我们直接多项式求导+求逆+积分解决。

时间复杂度：\(O(n\log n)\)，常数为\(6+3=9\)。

7.多项式求exp

前置：多项式求ln

现在，我们已知多项式\(A=A(x)\)（这样写是因为在这里把\(A\)视为是与\(x\)无关的），求\(F(x)=\exp(A)=e^{A}\)。只要我们设\(G(x)=\ln x-A\)，就得到：

\[G(F(x))=\ln F(x)-A=0 \]

我们考虑用牛顿迭代法来倍增解这个方程。

对于牛顿迭代法的初始解，即结果的常数项，我们并不知道具体值。但是如果不对的话，也只是缺少了一个常数罢了，那我们不妨设\(F(x)=1\)。

倍增：现在设我们已经求出了\(F(x)\)的前\(n\)项\(F_0(x)\)，即：

\[F_0(x)\equiv F(x)\pmod{x^n} \]

根据牛顿迭代法，我们求出下一个近似解为：

\[F(x)\equiv F_0(x)-\frac{G(F_0(x))}{G'(F_0(x))}\equiv F_0(x)-\frac{\ln F_0(x)-A}{F_0(x)^{-1}}\equiv F_0(x)(1-\ln F_0(x)+A(x)) \]

如此，就可以倍增实现了。

时间复杂度：\(O(n\log n)\)，常数：\(2\times(9+3)=24\)。

8.多项式求幂

已知多项式\(A(x)\)和指数\(k\)，求\(A(x)^k\)。

在幂数很大的时候，如果使用快速幂的思想，时间复杂度为\(O(n \log n\log k)\)，常数为\(6\)。当\(k\)很大时速度很慢，我们必须进行优化。

我们发现：

\[A(x)^k=\left(e^{\ln A(x)}\right)^k=e^{k \ln A(x)}=\exp(k \ln A(x)) \]

于是我们可以用多项式求ln+多项式求exp求出。

时间复杂度：\(O(n\log n)\)，常数：\(9+24=33\)。

9.时间复杂度总结

内容	时间复杂度	常数
多项式卷积	\(O(n\log n)\)	\(3\)
多项式求逆	\(O(n\log n)\)	\(6\)
多项式开根	\(O(n\log n)\)	\(18\)
多项式求导	\(O(n)\)	\(1\)
多项式积分	\(O(n)\)	\(1\)
多项式求ln	\(O(n\log n)\)	\(9\)
多项式求exp	\(O(n\log n)\)	\(24\)
多项式求幂	\(O(n\log n)\)	\(33\)

P.S. 快速插值坑着

7、代码实现

1.二进制反转

可以用一种类似dp的思想计算。

边界：\(0\)的二进制翻转为\(0\)

递归式：对于\(a\)，已经算出了\(rev_{\lfloor\frac{a}{2}\rfloor}\)，\(a\)就是除去最后一位的二进制翻转(\(rev_{\lfloor\frac{a}{2}\rfloor}\))向后移动一位再补上第一位。即：

rev[a]=(rev[a>>1]>>1)|((a&1)<<(l-1))

\(l\)为要翻转的位数。

2.复数类

套公式即可。

struct complex{
	double re,im;
	complex(double re=0,double im=0):re(re),im(im){}
	complex operator+(complex &b)const{return complex(re+b.re,im+b.im);}
	complex operator-(complex &b)const{return complex(re-b.re,im-b.im);}
	complex operator*(complex &b)const{return complex(re*b.re-im*b.im,re*b.im+im*b.re);}
};

3.FFT

• 1：根据二进制翻转交换\(a_r\)和\(a_{rev(r)}\)
• 2：枚举归并步长\(i\in[1,n)\)，\(i\)为二的幂；
  • 2.1： 根据欧拉公式求出\(\omega_{2 i}^1=\cos\frac{\pi}{i}+i\sin\frac{\pi}{i}\)
  • 2.2：枚举归并位置\(j\)，归并\([j,j+i)\)和\([j+i,j+2 i)\)，步长为\(2 i\)
    • 2.2.1：枚举\(x\)的幂数\(k\in[0,i)\)进行蝴蝶操作计算\(y\)，根据单位根计算\(\omega_i^k\)
      • 2.2.1.1：\(y_{j+k}=y_{j+k}+\omega_{2 i}^k y_{j+k+i}\)
      • 2.2.1.2：\(y_{j+k+i}=y_{j+k}-\omega_{2 i}^k y_{j+k+i}\)

注意：由于在C++中值会被更改，因此需要引入临时变量。

void FFT(complex c[]){
	for(int i=0;i<n;i++)if(i<r[i])swap(c[i],c[r[i]]);
	for(int i=1;i<n;i<<=1){
		complex omn(cos(pi/i),sin(pi/i));
		for(int j=0;j<n;j+=(i<<1)){
			complex om(1,0);
			for(int k=0;k<i;k++,om=om*omn){
				complex x=c[j+k],y=om*c[j+k+i];
				c[j+k]=x+y;
				c[j+k+i]=x-y;
			}
		}
	}
}

4.IFFT

由于公式中只差一个负号而已，因此引入一个参数\(type\)，在欧拉公式的地方乘上去，再除以\(n\)就可以了。

void FFT(complex c[],int tp=1){
    for(int i=0;i<n;i++)if(i<r[i])swap(c[i],c[r[i]]);
    for(int i=1;i<n;i<<=1){
        complex omn(cos(pi/i),tp*sin(pi/i));
        for(int j=0;j<n;j+=(i<<1)){
            complex om(1,0);
            for(int k=0;k<i;k++,om=om*omn){
                complex x=c[j+k],y=om*c[j+k+i];
                c[j+k]=x+y;
                c[j+k+i]=x-y;
            }
        }
    }
}
void IFFT(complex c[]){
	FFT(c,-1);
	for(int i=0;i<=m;i++)a[i].re/=n;
}

5.多项式乘法

模板：洛谷3083

注意：

1、由于FFT要求\(n\)为\(2\)的幂且结果的次数界较大，所以要把两个因式的系数补到\(l\)位，\(l\)满足\(l=2^t\)且\(l/2\)大于等于因式的次数界。

2、\(FFT\)虽然在数学上精准，但在C++中误差巨大，因此虚部不会为\(0\)，忽略即可。实部也不为正数，可以加上\(0.1\)再向下取整。

代码：

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
const double pi=acos(-1);
struct complex{
    double re,im;
    complex(double re=0,double im=0):re(re),im(im){}
    complex operator+(complex &b)const{return complex(re+b.re,im+b.im);}
    complex operator-(complex &b)const{return complex(re-b.re,im-b.im);}
    complex operator*(complex &b)const{return complex(re*b.re-im*b.im,re*b.im+im*b.re);}
}a[2097153],b[2097153];
int n,m,l,r[2097153];
void FFT(complex c[],int tp=1){
    for(int i=0;i<n;i++)if(i<r[i])swap(c[i],c[r[i]]);
    for(int i=1;i<n;i<<=1){
        complex omn(cos(pi/i),tp*sin(pi/i));
        for(int j=0;j<n;j+=(i<<1)){
            complex om(1,0);
            for(int k=0;k<i;k++,om=om*omn){
                complex x=c[j+k],y=om*c[j+k+i];
                c[j+k]=x+y;
                c[j+k+i]=x-y;
            }
        }
    }
}
void IFFT(complex c[]){
	FFT(c,-1);
	for(int i=0;i<=m;i++)a[i].re/=n;
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=0;i<=n;i++)scanf("%lf",&a[i].re);
    for(int i=0;i<=m;i++)scanf("%lf",&b[i].re);
    m+=n;
    for(n=1;n<=m;n<<=1)l++;
    for(int i=0;i<n;i++)r[i]=(r[i>>1]>>1)|((i&1)<<(l-1));
    FFT(a);
    FFT(b);
    for(int i=0;i<=n;i++)a[i]=a[i]*b[i];
    IFFT(a);
    for(int i=0;i<=m;i++)printf("%d ",int(a[i].re+0.5));
}

6.(I)FFT+(I)NTT

给出一个\(n\)次多项式和一个\(m\)次多项式的系数表达(\(1\le n,m\le 4000000\))，求乘积。\(type=0\)时，直接计算；\(type=1\)时，结果取模\(998244353\)(原根为\(3\))。

注：为了方便阅读，代码效率不高。若要提速，可以把单位根打表。而且，由于\(g^\frac{p-1}{n}\)中\(\frac{p-1}{n}\)必须为整数，故仅在第一个比\(n+m\)大的\(2\)的整数次幂是\(p-1\)的约数时才可行，此处\(998244353-1=998244352=119\times2^{23}\)，\(2^{23}=8388608>n+m\)。

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
using namespace std;
const double pi=acos(-1);
const int p=998244353;
typedef long long ll;
struct complex{
	double re,im;
	complex(double re=0,double im=0):re(re),im(im){}
	complex operator+(complex b)const{return complex(re+b.re,im+b.im);}
	complex operator-(complex b)const{return complex(re-b.re,im-b.im);}
	complex operator*(complex b)const{return complex(re*b.re-im*b.im,re*b.im+im*b.re);}
}af[131073],bf[131073];
struct modp{
	int a;
	modp(int a=0):a(a){}
	modp operator+(modp b)const{return (a+b.a)%p;}
	modp operator-(modp b)const{return (a-b.a+p)%p;}
	modp operator*(modp b)const{return ll(a)*b.a%p;}
	modp operator/(modp b)const{return (b^(p-2))*a;}
	modp operator^(int b)const{
		modp ans=1,bs=a;
		while(b){
			if(b&1)ans=ans*bs;
			bs=bs*bs;
			b>>=1;
		}
		return ans;
	}
}an[131073],bn[131073];
const modp g=3;
int n,m,l,r[131073],type;
modp gn[18];
void init(){
	m+=n;
	for(n=1;n<=m;n<<=1)l++;
	for(int i=0;i<n;i++)r[i]=(r[i>>1]>>1)|((i&1)<<(l-1));
	for(int i=0;i<=17;i++)gn[i]=g^((p-1)/(1<<i));
}
void FFT(complex c[],int tp=1){
	for(int i=0;i<n;i++)if(i<r[i])swap(c[i],c[r[i]]);
	for(int i=1;i<n;i<<=1){
		complex omn(cos(pi/i),tp*sin(pi/i));
		for(int j=0;j<n;j+=(i<<1)){
			complex om(1,0);
			for(int k=0;k<i;k++,om=om*omn){
				complex x=c[j+k],y=om*c[j+k+i];
				c[j+k]=x+y;
				c[j+k+i]=x-y;
			}
		}
	}
}
void IFFT(complex c[]){
	FFT(c,-1);
	for(int i=0;i<=n;i++)c[i].re/=n;
}
void NTT(modp c[],int tp=1){
	for(int i=0;i<n;i++)if(i<r[i])swap(c[i],c[r[i]]);
	for(int i=1,id=1;i<n;i<<=1,id++){
		modp ggn=gn[id]^(tp==1?1:p-2);
		for(int j=0;j<n;j+=(i<<1)){
			modp gg=1;
			for(int k=0;k<i;k++,gg=gg*ggn){
				modp x=c[j+k],y=gg*c[j+k+i];
				c[j+k]=x+y;
				c[j+k+i]=x-y;
			}
		}
	}
}
void INTT(modp c[]){
	NTT(c,-1);
	for(int i=0;i<=n;i++)c[i]=c[i]/n;
}
int main(){
	scanf("%d%d%d",&n,&m,&type);
	if(type==0){
		for(int i=0;i<=n;i++)scanf("%lf",&af[i].re);
		for(int i=0;i<=m;i++)scanf("%lf",&bf[i].re);
	}else{
		for(int i=0;i<=n;i++)scanf("%d",&an[i].a);
		for(int i=0;i<=m;i++)scanf("%d",&bn[i].a);
	}
	init();
	if(type==0){
		FFT(af);
		FFT(bf);
		for(int i=0;i<=n;i++)af[i]=af[i]*bf[i];
		IFFT(af);
		for(int i=0;i<=m;i++)printf("%d ",int(af[i].re+0.5));
	}else{
		NTT(an);
		NTT(bn);
		for(int i=0;i<=n;i++)an[i]=an[i]*bn[i];
		INTT(an);
		for(int i=0;i<=m;i++)printf("%d ",an[i].a);
	}
	printf("\n");
}

常数只有上面那个的三分之一的NTT（正式考试请务必采用这种写法）：

PS:有一道题上面那个3700ms,这个1000ms

inline ll pow(ll a,int b){
	ll ans=1;
	while(b){
		if(b&1)ans=ans*a%p;
		a=a*a%p;
		b>>=1;
	}
	return ans;
}
inline ll add(ll a,ll b){return a+b>p?a+b-p:a+b;}
inline ll cut(ll a,ll b){return a-b<0?a-b+p:a-b;}
void init(){
	for(n=1;n<=s;n<<=1);
	nn=n;
	gn[0][0]=gn[1][0]=1;
	gn[0][1]=pow(g,(p-1)/(n<<1));
	gn[1][1]=pow(gn[0][1],p-2);
	for(int i=2;i<(n<<1);i++){gn[0][i]=gn[0][i-1]*gn[0][1]%p;gn[1][i]=gn[1][i-1]*gn[1][1]%p;}
	inv[1]=1;
	for(int i=2;i<=(n<<1);i++)inv[i]=inv[p%i]*(p-p/i)%p;
}
void NTT(ll c[],int n,int tp=1){
	for(int i=0;i<n;i++){
		r[i]=(r[i>>1]>>1)|((i&1)*(n>>1));
		if(i<r[i])swap(c[i],c[r[i]]);
	}
	for(int i=1;i<n;i<<=1){
		for(int j=0;j<n;j+=(i<<1)){
			for(int k=0;k<i;k++){
				ll x=c[j+k],y=gn[tp!=1][nn/i*k]*c[j+k+i]%p;
				c[j+k]=add(x,y);
				c[j+k+i]=cut(x,y);
			}
		}
	}
}
void INTT(ll c[],int n){
	NTT(c,n,-1);
	for(int i=0;i<n;i++)c[i]=c[i]*inv[n]%p;
}

7.任意模数FFT

给定\(n,m,P\)，再给定次数界为\(n\)的第一个多项式和次数界为\(m\)的第二个多项式，求两个多项式的卷积模\(P\)。

注意：拆系数FFT精度损失极大，需要使用long double保证正确性。

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
using namespace std;
typedef long long ll;
int x,n,m,l,r[262145],pm,p;
const long double pi=acos(-1);
struct complex{
	long double re,im;
	complex(long double re=0,long double im=0):re(re),im(im){}
	complex operator+(const complex &b)const{return complex(re+b.re,im+b.im);}
	complex operator-(const complex &b)const{return complex(re-b.re,im-b.im);}
	complex operator*(const complex &b)const{return complex(re*b.re-im*b.im,re*b.im+im*b.re);}
}k1[262145],r1[262145],k2[262145],r2[262145],c1[262145],c2[262145],c3[262145];
void FFT(complex c[],int tp=1){
	for(int i=0;i<n;i++)if(i<r[i])swap(c[i],c[r[i]]);
	for(int i=1;i<n;i<<=1){
		complex omn(cos(pi/i),tp*sin(pi/i));
		for(int j=0;j<n;j+=(i<<1)){
			complex om(1,0);
			for(int k=0;k<i;k++,om=om*omn){
				complex x=c[j+k],y=om*c[j+k+i];
				c[j+k]=x+y;
				c[j+k+i]=x-y;
			}
		}
	}
}
void IFFT(complex c[]){
	FFT(c,-1);
	for(int i=0;i<=n;i++)c[i].re/=n;
}
void init(){
	m+=n;
	for(n=1;n<=m;n<<=1)l++;
	for(int i=0;i<n;i++)r[i]=(r[i>>1]>>1)|((i&1)<<(l-1));
}
int main(){
	scanf("%d%d%d",&n,&m,&p);
	pm=sqrt(p);
	for(int i=0;i<=n;i++){
		scanf("%d",&x);
		k1[i]=x/pm;
		r1[i]=x%pm;
	}
	for(int i=0;i<=m;i++){
		scanf("%d",&x);
		k2[i]=x/pm;
		r2[i]=x%pm;
	}
	init();
	FFT(k1);
	FFT(r1);
	FFT(k2);
	FFT(r2);
	for(int i=0;i<=n;i++){
		c1[i]=k1[i]*k2[i];
		c2[i]=k1[i]*r2[i]+r1[i]*k2[i];
		c3[i]=r1[i]*r2[i];
	}
	IFFT(c1);
	IFFT(c2);
	IFFT(c3);
	for(int i=0;i<=m;i++){
		ll s1=ll(c1[i].re+0.5)%p*pm%p*pm%p,s2=ll(c2[i].re+0.5)%p*pm%p,s3=ll(c3[i].re+0.5)%p;
		printf("%lld ",((s1+s2)%p+s3)%p);
	}
}

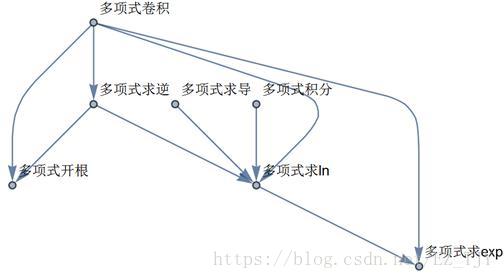
7.多项式的运算

依赖关系：

直接按照公式打就好了。

我们先修改NTT：

void NTT(modp c[],int n,int tp=1){
	for(int i=0;i<n;i++){
		r[i]=(r[i>>1]>>1)|((i&1)*(n>>1));
		if(i<r[i])swap(c[i],c[r[i]]);
	}
	for(int i=1,id=1;i<n;i<<=1,id++){
		modp ggn=gn[id]^(tp==1?1:p-2);
		for(int j=0;j<n;j+=(i<<1)){
			modp gg=1;
			for(int k=0;k<i;k++,gg=gg*ggn){
				modp x=c[j+k],y=gg*c[j+k+i];
				c[j+k]=x+y;
				c[j+k+i]=x-y;
			}
		}
	}
}
void INTT(modp c[],int n){
	NTT(c,n,-1);
	for(int i=0;i<n;i++)c[i]=c[i]/n;
}

求逆：

void inverse(modp c[],int n=n){
	static modp t[262145],tma[262145];
	t[0]=c[0]^(p-2);
	for(int k=2;k<=n;k<<=1){
		for(int i=0;i<(k<<1);i++)tma[i]=(i<k?c[i]:0);
		for(int i=(k>>1);i<(k<<1);i++)t[i]=0;
		NTT(tma,k<<1);
		NTT(t,k<<1);
		for(int i=0;i<(k<<1);i++)t[i]=t[i]*2-t[i]*t[i]*tma[i];
		INTT(t,k<<1);
	}
	memcpy(c,t,sizeof(int)*n);
}

开根(\(c[0]=1\))：

void sqrt(modp c[],int n=n){
	static modp t[262145],tma[262145],tmb[262145];
	t[0]=1;
	for(int k=2;k<=n;k<<=1){
		for(int i=0;i<k;i++)tma[i]=t[i]*2;
		inverse(tma,k);
		for(int i=0;i<(k<<1);i++)tmb[i]=(i<k?c[i]:0);
		NTT(tma,k<<1);
		NTT(tmb,k<<1);
		for(int i=0;i<(k<<1);i++){
			modp tmp=tma[i];
			tma[i]=t[i];
			t[i]=tmp*tmb[i];
		}
		INTT(t,k<<1);
		for(int i=0;i<(k<<1);i++)t[i]=(i<k?t[i]+tma[i]/2:0);
	}
	memcpy(c,t,sizeof(int)*n);
}

求导：

void derivative(modp c[],int n=n){for(int i=0;i<n;i++)c[i]=c[i+1]*(i+1);}

积分：

void integrate(modp c[],int n=n){for(int i=n-1;i>=1;i--)c[i]=c[i-1]*inv[i];c[0]=0;}

求ln：

void ln(modp c[],int n=n){
	static modp t[262145];
	for(int i=0;i<(n<<1);i++)t[i]=(i<n?c[i]:0);
	derivative(t,n);
	inverse(c,n);
	NTT(t,n<<1);
	NTT(c,n<<1);
	for(int i=0;i<(n<<1);i++)c[i]=c[i]*t[i];
	INTT(c,n<<1);
	for(int i=n;i<(n<<1);i++)c[i]=0;
	integrate(c,n);
}

求exp：

void exp(modp c[]){
	static modp t[262145],ta[262145];
	t[0]=1;
	for(int k=2;k<=n;k<<=1){
		for(int i=0;i<(k<<1);i++)ta[i]=t[i];
		ln(ta,k);
		for(int i=0;i<k;i++)ta[i]=c[i]-ta[i];
		ta[0].a++;
		NTT(t,k<<1);
		NTT(ta,k<<1);
		for(int i=0;i<(k<<1);i++)t[i]=t[i]*ta[i];
		INTT(t,k<<1);
		for(int i=k;i<(k<<1);i++)t[i]=0;
	}
	memcpy(c,t,sizeof(modp)*n);
}

求幂：
我们在多项式求exp中假定了\(c[0]=1\)，那么如果常数项不是\(1\)的话我们就把常数项变为\(1\)在运算后再用快速幂变回来即可。

void pow(modp c[],int k){
	ln(c);
	for(int i=0;i<n;i++)c[i]=c[i]*k;
	exp(c);
}

8、拉格朗日反演

1.形式幂级数

对于任意一个域\(F\)我们定义在其上的形式幂级数为：

\[f(x)=\sum_{k=0}^\infty a_k x^k,a_k\in F \]

记所有的形式幂级数为\(F[[x]]\)。

2.反演公式

拉格朗日反演是求关于函数方程的幂级数展开系数非常重要的工具，可以用于组合计数函数的系数提取。

公式内容：

这里\([x^n]f(x)\)指取\(f(x)\)中\(x^n\)的系数。

若\(f(x),g(x)\in F[[x]]\)且\(f(g(x))=x\)，则称\(f(x)\)为\(g(x)\)的复合逆。满足：

\[[x^n]g(x)=\frac{1}{n}[x^{-1}]\frac{1}{f(x)^n}\tag{1} \]

特别的，如果\(f(x)=\displaystyle\frac{x}{\phi(x)}\)，那么有：

\[[x^n]g(x)=\frac{1}{n}[x^{n-1}]\phi(x)^n\tag{2} \]

公式的推导：
由式\(f(x)=\displaystyle\frac{x}{\phi(x)}\)，得\(\phi(x)=\displaystyle\frac{x}{f(x)}\)，代入\((2)\)式可得：

\[[x^n]g(x)=\frac{1}{n}[x^{n-1}]\left(\frac{x}{f(x)}\right)^n \]

公式的推广：

\[[x^n]h(g(x))=\frac{1}{n}[x^{n-1}]h'(x)\left(\frac{x}{f(x)}\right)^n \]