1252. 奇数值单元格的数目

题目描述：

　　给你一个 m x n 的矩阵，最开始的时候，每个单元格中的值都是 0。另有一个二维索引数组 indices，indices[i] = [ri, ci] 指向矩阵中的某个位置，其中 ri 和 ci 分别表示指定的行和列（从 0 开始编号）。

　　对 indices[i] 所指向的每个位置，应同时执行下述增量操作：

• ri 行上的所有单元格，加 1 。
• ci 列上的所有单元格，加 1 。

　　给你 m、n 和 indices 。请你在执行完所有 indices 指定的增量操作后，返回矩阵中 奇数值单元格 的数目。

 

示例：

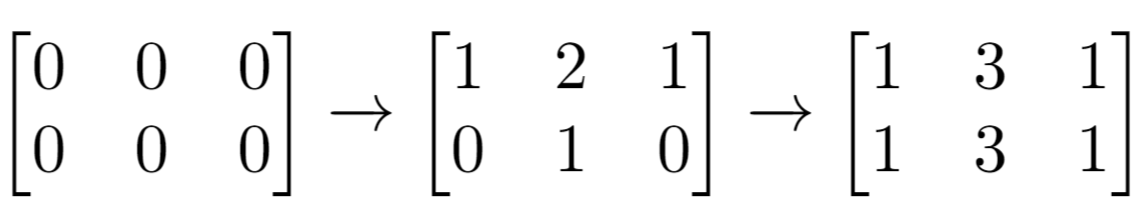
输入：m = 2, n = 3, indices = [[0,1],[1,1]]
输出：6
解释：最开始的矩阵是 [[0,0,0],[0,0,0]]。
第一次增量操作后得到 [[1,2,1],[0,1,0]]。
最后的矩阵是 [[1,3,1],[1,3,1]]，里面有 6 个奇数。

 

解题思路：

• 每次操作都会使整一行或整一列加1，我们可以一个行数组 row[m] 与一个列数组 column[n] 来记录每一行和每一列操作的次数。
• 而对于给定 m × n 数组中的某个位置（x,y），操作次数为偶数的时候，它的值就为偶数，不计入最后奇数单元格的统计中。如示例第二步中的“2”。因此最后统计航数组 row[m] 与列数组 column[n] 时，我们只关心操作次数为奇数的行和列。

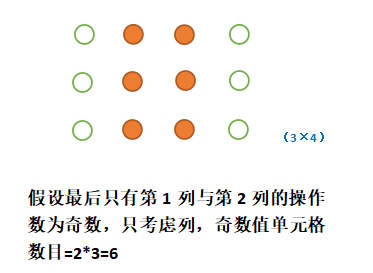
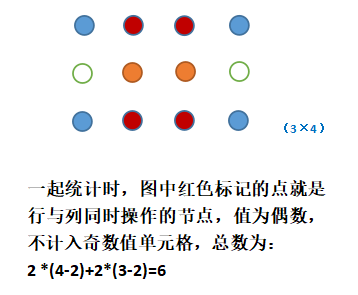
　　如下图所示，不考虑列的情况，我们计算操作次数为奇数的行数 odd_row 时，总的奇数值单元格应为：odd_row * n(列数)；同理，不考虑行的情况，计算操作次数为奇数的列数 odd_colum 时，奇数单元格为：odd_colunm *m(行数)。但同时统计行与列时，从行的视角中看，应该剔除 odd_colum 的列；列视角同理。也即，

　　总数 = odd_row * (n - odd_column) + odd_column * (m - odd_row)

 

 

 

 

代码实现：

/**
 * @param {number} m
 * @param {number} n
 * @param {number[][]} indices
 * @return {number}
 */
var oddCells = function(m, n, indices) {
    let row = new Array(m).fill(0);
    let column = new Array(n).fill(0);
    for(let i=0;i<indices.length;i++){
        row[indices[i][0]]++;
        column[indices[i][1]]++;
    }
    let odd_row = 0;
    for(let i=0;i<m;i++){
        if(row[i]%2!==0){
            odd_row++;
        }
    }
    let odd_column = 0;
    for(let i=0;i<n;i++){
        if(column[i]%2!==0){
            odd_column++;
        }
    }
    return (odd_row*(n-odd_column)+odd_column*(m-odd_row));
};