stl_list::sort算法分析

前言

看SGI list的源码过程中，对内置sort算法看了半天没看懂，找了很多资料算是初步理解其原理，遂写下此文以记录。stl_list被实现为环状的双向链表，设置一个“哨”node作为end()。list不能使用标准sort算法，因为STL算法sort只接受RandonAccessIterator，必须使用自身的sort。

sort原理

list::sort本质上是mergesort，侯捷的理解是错的，但采用一种特殊的形式。

普通的mergesort直接将待排序的序列一分为二，然后各自递归调用mergesort，再使用merge算法将已完成排序的两个子序列归并，总时间效率是O(n*lgn)。mergesort是很好的排序算法，效率高，但在内存中的排序算法中不常见，主要是空间消耗太多，也是O(n)。

但对于链表而已，用普通的mergesort每次找到中间元素再一分为二的代价实在太大，对list这种非randomAccess的容器。list::sort所使用的mergesort形式上大不一样：将前两个元素合归并，再将后两个元素归并，归并这两个子序列称为四个元素的有序子序列；重复这一过程，得到8个元素的子序列，16个的，32个的., ...，知道处理完成，主要调用swap和merge函数。list::sort中预留64个temp_list，所以最多可以处理2^64-1个元素的序列，这应该足够。

sort源码

下面是SGI list::sort的源码，里面用到的splice，swap和merge函数比较简单，只要去看就能看懂，这里不再赘述。算法的巧妙之处在于外层while循环下counter链表数组的维护，这个比价难理解，需要认真推敲代码运行过程的行为，这里我很难用文字描述清楚。我觉得借助下面的调试分析代码可以有效帮助理解这个过程，这里我就不再大篇幅描述。

template<class T, class Alloc>
void list<T, Alloc>::sort() {
    if (node->next == node || link_type(node->next)->next == node) return;
    list<T, Alloc> carry;       //辅助链表，相当与tmp
    list<T, Alloc> counter[64]; //保存当前递归层次的结果，第i链表保存的元素个数为2的i次方或0
    int fill = 0;
    while (!empty()) {
        carry.splice(carry.begin(), *this, begin());  //将链表的第一个元素移动至carry开头
        int i = 0;
        //从小到大不断合并非空归并层次直至遇到空层或者到达当前最大归并层次
        while (i < fill && !counter[i].empty()) {
            counter[i].merge(carry);  //合并链表，结果链表是有序的，必须保证合并前两链表有序
            carry.swap(counter[i++]); //链表元素互换
        }
        carry.swap(counter[i]);  //将carry元素放到counter[i]中，相当于将carry情况，带下一次循环使用
        if (i == fill) ++fill;
    }
    //将所有归并层次的结果合并得到最终结果counter[fill-1]
    for (int i = 1; i < fill; ++i) counter[i].merge(counter[i-1]);
    swap(counter[fill-1]);
}

调试分析

为理解上述实现原理，我专门在stl_list容器外实现了一个完全和list::sort原理一样的函数，该函数会在每一次循环将所有递归层次的内容打印处理，方便分析理解。具体测试代码如下：

template<class T>
void print(const STD::list<T>& list) { //打印链表
    for (auto it = list.begin(); it != list.end(); ++it) {
        std::cout << *it << " ";
    }
    std::cout << std::endl;
}

template<class T>
void sort(STD::list<T>& list) {
    if (list.size() <= 1) return;
    STD::list<T> carry;
    STD::list<T> counter[64];
    int fill = 0;
    while (!list.empty()) {
        carry.splice(carry.begin(), list, list.begin());
        int i = 0;
        while (i < fill && !counter[i].empty()) {
            counter[i].merge(carry);
            carry.swap(counter[i++]);
        }
        carry.swap(counter[i]);
        if (i == fill) ++fill;
        
        //打印本次循环的所有递归层次内容
        std::cout << "---------test------------------" << std::endl;
        for (int i = 0; i < fill; ++i) {
            std::cout << "counter[" << i << "]: ";
            print(counter[i]);
        }
    }

    for (int i = 1; i < fill; ++i) counter[i].merge(counter[i-1]);
    list.swap(counter[fill-1]);
}

void list_test() {
    STD::list<int> list;
    for (int i=0; i<10; ++i) {
        int r = rand() % 10;
        list.push_back(r);
    }
    
    STD::list<int>::iterator iter = list.begin();
    for ( ; iter != list.end(); ++iter) {
        std::cout << *iter << " ";
    }
    std::cout << std::endl;
    std::cout << "begin sort:" << std::endl;
    sort(list);
    std::cout << "after sort:" << std::endl;
    iter = list.begin();
    for ( ; iter != list.end(); ++iter) {
        std::cout << *iter << " ";
    }
    std::cout << std::endl;
}

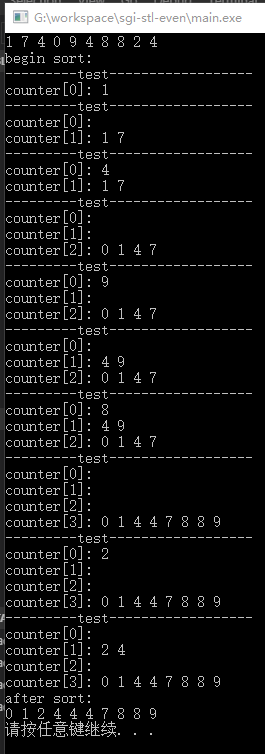
调用list_test函数的运行结果如下，验证上述分析过程是正确的。