WQS二分

WQS 二分取消一类题目的限制条件，代价是 \(O(\log n)\) 的时间复杂度。

首先，WQS二分用于解决什么问题？

我们先看一个难题：

题目

有一个 \(n\) 个数的数组 \(a\)。
求在 \(a\) 中恰好选择 \(m\) 个数的情况下，选择的数的和的最大值。

现在看到了这个题目，你发现你不会排序，不会贪心。好难啊，你想。

你打算用另一种方式解决这题。

做法

我们定义 \(g(x)\) 为恰好选择 \(x\) 个数的情况下，选择的数的和的最大值。

经过观察，我们发现 \(g(x)\) 是一个凸函数。

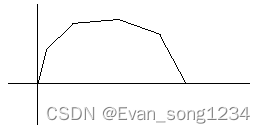
这表明，\(g(x)\) 只有一个最大值（在本题中，就是把所有正数都取了的情况）。

如果取消 \(m\) 的限制，肯定会取最大值 \(g_{max}\)。

但你取不到，因为不一定恰好有 \(m\) 个正数。

那么我们考虑如何做出改变去取消 \(m\) 这个限制。

尝试给选择数一个惩罚（或奖励） \(k\)，我们每次选择一个数，答案就增加 \(k\)。（\(k\in \mathbb{R}\) ）

于是，这个函数 \(g(x)\) 就转变成 \(f(x) = g(x) + kx\) 了。

显然，当 \(k\) 取值增大，\(f(x)\) 的最大值取值位置 \(x_0\) 就会增大。当 \(k\) 取值减少，\(x_0\) 会减小。

而我们能够轻而易举的对于每个 \(k\) 计算 \(f(x)\) 最大值 \(f(x_0)\) 和其取值位置 \(x_0\)（\(O(n)\)）。

注意：由于 \(f(x)\) 是选择 \(x\) 个时（附带了惩罚）的最大值，那么 \(f(x)\) 的最大值就是选择任意个的最大值，相当于取消了最大值限制。

所以，我们可以二分 \(k\)，根据当前 \(k\) 下 \(f(x)\) 最大值取值位置与题目限制 \(m\) 的大小关系来更改 \(k\)。

最终可以获得最大值取值位置为 \(m\) 时的 \(k\) 和 \(f(m)\)。

然后通过 \(f(x) = g(x) + kx\)，可以反推出 \(g(m) = f(m) - km\)。

即可得出答案，时间复杂度 \(O(n\log n)\)。

\[\]

我们可以用函数的角度再来讲解一遍 wqs 二分。

同样的，我们设 \(g(x)\) 为限制为 \(x\) 时的答案，根据前提，\(g(x)\) 为一个凸函数。

所以说，\(g(x)\) 的导数 \(g'(x)\)（可以理解为在 \(x\) 处的切线斜率），有单调性。

我们二分斜率 \(k\)，然后求出切线斜率为 \(k\) 的点的 \(y\) 坐标，最终切点 \(x\) 坐标为 \(m\) 时的 \(y\) 就是答案。

我们假设这条斜率为 \(k\) 的切线的方程为 \(y=kx+b\)。

我们需要求出切 \(b\) 和 \(x\)。其中，\(b = y - kx\)。（回到原来的那个式子了）

可以发现，如果函数为上凸（如一开始的图），那么切线的截距 \(b\)（方程里的 \(b\)），就是和函数有交点的所有斜率为 \(k\) 的直线的截距的最大值。

由于切点的横坐标只可能是整数，所以我们的切线的截距

\[b = \max\limits_{y=g(x),x\in\mathbb{Z}}\{y - kx\} \]

即

\[b = \max\limits_{x\in\mathbb{Z}}\{g(x) - kx\} \]

于是我们要求 \(\max\{g(x) - kx\}\)，容易发现，可以看成给每个数的权值减去 \(k\) 之后，去掉最大值的答案。

为了方便理解，我们再来一道题（一道需要用到WQS二分的题目）。

题目

有一张 \(n\) 个点，\(m\) 条带权边的图 \(G\)，每条边权值为 \(w_i\)。
求图 \(G\) 的生成树的最大权值和，满足点 \(s\) 恰好选择 \(t\) 条边。

首先发现本题难以使用 \(dp\) 之类算法来做。

其次，本题取消限制后极其容易（就是个最大生成树）。

最后，容易发现 ，关于 \(t\) 的函数 \(g(t)\) 代表选择 \(t\) 条时的答案，是一个凸函数。

我们就可以使用WPS二分以 \(O(\log n)\) 的代价换取取消限制。

做法

还是一样，我们取消限制，然后增加奖励或惩罚 \(k\)。

根据取最大值位置与 \(t\) 的关系，二分惩罚 \(k\)，直接使用最小生成树 \(O(n)\) 来计算惩罚为 \(k\) 时最大值。

最终可以得出在一定惩罚下，取 \(m\) 条边时的最大值。我们只需要减去惩罚即可。

也可以换一种方法理解。

我们将 \(g(x)\) 的图像画出，是一个凸函数。

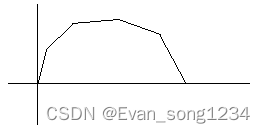
我们现在需要求 \(x=t\) 时的取值 \(g(t)\)。

我们发现对于每个在 \(g(x)\) 上的点 \((x, g(x))\)，都存在一个斜率 \(k\)，使得经过这个点的斜率为 \(k\) 的直线 \(l\) 能与 \(g(x)\) 相切。

因为 \(g(x)\) 是一个凸函数，所以随着 \(x\) 的增大，\((x, g(x))\) 对应斜率 \(k\) 会随之增大。

所以我们可以通过二分斜率 \(k\)，来求出 \(x=t\) 时的取值 \(g(t)\)。

对于每次二分的斜率 \(k\)，我们要求 \(g(x)\) 中切线斜率为 \(k\) 的切点。我们设直线 \(l\) 的 \(y\) 轴截距为 \(f(x)\)，代表斜率为 \(k\) 的直线 \(l\) 经过点 \((x, g(x))\) 时的 \(y\) 轴截距。

则 \(g(x) = kx + f(x)\)。

容易发现，当 \(f(x)\) 取到最大值时，\(y=kx+f(x)\) 就会与 \(g(x)\) 函数相切，切点则是此时的 \((x, g(x))\)

所以我们尝试求出 \(f(x)\) 最大值，从 \(g(x) = kx + f(x)\) 可得 \(f(x) = g(x) - kx\)。

这个式子可以感性理解为：\(f(x)\) 为将与 \(s\) 相连的边中所选的 \(x\) 条边的权值都减少 \(k\) 时，选择 \(x\) 条边时的生成树的最大权值和。

所以 \(f(x)\) 中最大值则为：将与 \(s\) 相连的边中所选的边的权值都减少 \(k\) 时，最大生成树的权值和。

所以我们可以非常容易的求出 \(f(x)\) 最大值，和取得最大值时选择的边数 \(x\)。

我们就可以开始二分了。

对于最终求出的 \(f(t)\)，我们可以根据 \(g(x) = kx + f(x)\)，求出 \(g(t)\)。

总结

经过上面几题可以发现，WQS二分适用于符合一下几点的问题：

• 有一个恰好选择的个数限制 \(m\)
• 代表恰选 \(x\) 个时答案的函数 \(g(x)\) 需要为凸函数。
• 取消限制 \(k\) 后问题可以快速计算。

解决时，一般选取一个附值 \(k\)，使得每多选一次，最终答案就增加 \(k\)。然后计算当附值为 \(k\) 时的最大值取值位置 \(x_0\)。将其与限制 \(m\) 像比较。由于函数是凸函数，附值为 \(k\) 时的取最大值位置 \(h(k) =x_0\) 有单调性。所以可以二分 \(k\) 让 \(x_0\) 靠近 \(m\)，最终计算得当附值为 \(k_0\) 是取最大值位置 \(h(k_0)=m\) 时。再将附值为 \(k_0\) 时的最大值减去 \(k\times m\) 即可。