后缀数组

前言

后缀数组 \(SA\) 可以用于各方面字符串问题（最长公共子串等），其目的是求出这个字符串的所有后缀按照字典序的排名。

本篇博客使用 \(s_{l,r}\) 表示字符串 \(s\) 在下标 \(l\) 到 \(r\) 内的所有字符组成的子串，用 \(|s|\) 表示字符串 \(s\) 的大小。

例如 \(s=^"abc^"\) 则 \(s_{1,2}=^"bc^", |s|=3\)

算法复杂度

时间 \(O(|s|\log |s|)\)

空间 \(O(|s|)\)

算法思路

显而易见，把字符串所有后缀按照字典序排序后，就可以求得任意后缀的排名。排序的时间复杂度为 \(O(|s|\log |s|)\)

但是，我们无法将所有后缀都依次储存，因为这样空间复杂度为 \(O(|s|^2)\)。

所以考虑使用其他方法。

后缀数组需要求两个数组：后缀数组 \(SA\) 和排名数组 \(rank\)

\(SA_i\) 代表从第 \(i\) 个字符开始的后缀的排名。

\(rank_i\) 代表排名为 \(i\) 的后缀的开始字符的下标。

所以，\(SA_i = j\) 时，\(rank_j = i\)。

对于后缀数组的计算，主要有两种算法：

• 倍增算法

• DC3算法

这篇博客只讲倍增（主要是DC3我不会）。

倍增算法的思路主要是递推，从之前的排名推出之后的排名。

我们假设要求字符串 \(s\) 的 \(SA\) 数组。

我们先求出每个后缀按照第一个字符的排序的 \(rank\)（若第一个字符相同，则 \(rank\) 相等），

即每个 i 对应的 \(s_{i, i}\) 在所有 \(s_{i, i}\) 中的排名。

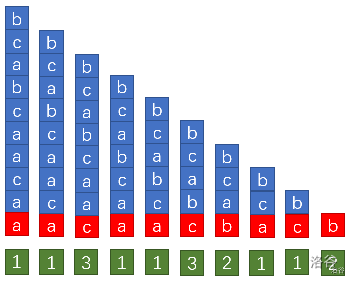
然后用所得出的 \(rank\) 来计算出所有后缀按照前两个字符排序的 \(rank\)（每个 \(i\) 对应的 \(s_{i, i + 2^1 - 1}\) 在所有 \(s_{i, i + 2^1 - 1}\) 中的排名。）

接着是四个，八个...，直到全部字符。（每个 \(i\) 对应的 \(s_{i, i + 2^k - 1}\) 在所有 \(s_{i, i + 2 ^ k - 1}\) 中的排名。）

算法流程

假设当前我们要计算后缀按照前 \(2^k\) 个字符排序的 \(rank\)。而我们已经求出了按前 \(2^{k-1}\) 个字符排序的 \(rank\)。

那么对于每个 \(p\)，我们要求的就是 \(s_{p, p + 2 ^ {k} - 1}\) 在所有 \(s_{i, i + 2 ^ {k} - 1]}\) 的排名。

于是考虑 \(s_{i, i + 2 ^ {k - 1} - 1}\) 和 \(s_{p, p + 2^{k} - 1]}\) 之间的关系。

发现 \(s_{p, p + 2^{k} - 1} = s_{p, p+2^{k-1}-1} + s_{p+2^{k-1}, p+2^{k}}\)。

而 \(s_{p, p + 2 ^ {k - 1} - 1}\) 和 \(s_{p + 2 ^ {k - 1}, p + 2 ^ {k}]}\) 的排名我们都已经求过了。

即 \(rank_p\) 和 \(rank_{p + 2 ^ {k - 1}}\)。

我们把所有 \(rank_{i}\) 和 \(rank_{i + 2 ^ {k - 1}}\) 合并形成 \(n\) 个二元组（第 \(i\) 个二元组是 \(rank_{i}\) 和 \(rank_{i+ 2 ^{k-1}}\) 的组合，表示 \(s_{i, i + 2 ^ {k} - 1}\)）。

然后对于这个二元组排序，于是就可以得出新的 \(rank_i\)。

重复这个步骤，直到所有 \(rank_i\) 都不相同为止。然后求出来的 \(rank\) 就是我们要求的排名数组的。

我们需要求 \(\log n\) 的 \(rank\)，每次求需要 \(O(n\log n)\) 的快速排序时间，所以总时间复杂度是 \(O(n\log^2n)\)。

算法优化

一、基数排序优化

\(rank\) 数组里的数一定在 \([1, n]\) 的范围内，所以我们可以使用基数排序来代替快速排序。

二元组基数排序，我们需要先把第二关键字放进桶中，然后从小到大枚举每个桶，把桶里的数按照放进去的顺序挨个取出来，

再把第一关键字放进去，同样取出来，然后得到的数组就是排好序的了。

基数排序复杂度是 \(O(n)\) 的，优化后算法时间复杂度为 \(O(n\log n)\) 了。

算法应用

最长公共前缀（LCP）

\(SA\) 数组还有一种基础操作：给定两个后缀的起始字符串，求他们最长公共前缀的长度。

我们可以 \(O(n)\) 快速求出排序后相邻两个后缀的最长公共前缀的长度。

我们让 \(height_i\) 代表 \(SA_{i - 1}\) 和 \(SA_i\) 对应的两个后缀的最长公共前缀的长度。

然后，我们可以得到两个后缀的排名 \(rank_i, rank_j\)，然后我们只需要求出 \(\min\limits_{i+1\leq x\leq j}\{height_i\}\)

只需预处理然后使用 \(RMQ\) 即可。

最长公共子串（LCS）

求 \(n\) 个串的最长公共子串

此问题可以转化为求一些后缀的最长公共前缀的最大值，这些后缀应分属于 \(n\) 个串。

具体方法如下：

设 \(n\) 个串分别为 \(s_1,…, s_n\)，首先建立一个串 \(S\)，把这 \(n\) 个串用不同的分隔符连接起来。

\[S = s_1 + p_1 + s_2 + p_2 + s_3 + ... + s_{n-1} + p_{n-1} + s_n \]

这些分隔符应是 \(n - 1\) 个与 \(s_1, s_2, ..., s_n\) 都不相同的字符。

因为需要保证 \(S\) 的后缀的公共前缀不会跨出一个原串的范围。（当然你也可以用其他方法来避免）

接下来，求出字符串 \(S\) 的 \(SA\) 数组和 \(height\) 数组。

二分枚举答案 \(ans\)，于是问题就转化成 \(n\) 个串是否可以有长度为 \(ans\) 的公共字串，而代价是，我们多出来了一个 \(O(\log \max\limits_{1\leq i \leq n}\{|s_i|\})\) 的时间复杂度。

如果能找出 \(height\) 数组中连续的一段 \([i,j]\)，满足排完序的后缀中第 \([i, j]\) 个后缀的起始字符分别属于 \(\{S_1,…,S_n\}\) 中的每个字符串，使得

\[\min_{k \in [i + 1, j]}\{height[k]\}>= ans \]

那么 \(ans\) 就是可行解，否则不是。

具体查找 \([i, j]\) 时，可以使用类似双指针的技巧，先从前到后枚举 \(i\) 的位置，如果发现 \(height_i >= ans\)，则开始从 \(i\) 向后枚举 \(j\) 的位置，直到找到了 \(height_{j+1}< ans\)，判断是否满足上述情况。

如果满足，则 \(ans\) 为可行解，然后直接返回，否则令 \(i = j + 1\) 继续向后枚举。

\(S\) 中每个字符被访问了 \(1\) 次，\(S\) 的长度为 \(\sum\limits_{i=1}^{n}(|s_i|+1)-1\)，所以时间复杂度为 \(O(\sum\limits_{i=1}^{n}|s_i|)\)。

算法伪代码

暂无