时间复杂度和空间复杂度详解

一,思维导图

 

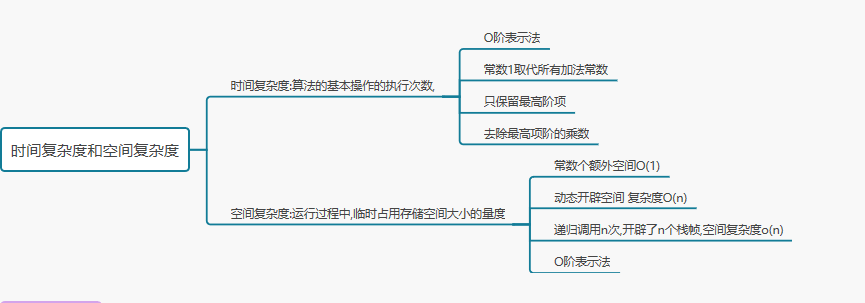
 二,定义

    时间复杂度的定义：在计算机科学中，算法的时间复杂度是一个函数，它定量描述了该算法的运行时间。一个算法执行所耗费的时间，从理论上说，是不能算出来的，只有你把你的程序放在机器上跑起来，才能知道。但是我们需要每个算法都上机测试吗？是可以都上机测试，但是这很麻烦，所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例，算法中的基本操作的执行次数，为算法的时间复杂度。

空间复杂度定义:空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度 。空间复杂度不是程序占用了多少bytes的空间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟实践复杂度类似，也使用大O渐进表示法。

 三,具体计算

 1,冒泡排序的时间复杂度计算和空间复杂度计算

   时间复杂度O(N^2)  最好执行n次,最坏执行(n*(n+1))/2  所以按照思维导图解决方案   时间复杂度O(N^2) 

   空间复杂度O(1)      使用了常数个额外空间  所以复杂度为O(1)

#include <stdio.h>

int main()

{
 
int a[10]={0,1,2,3,4,5,6,7,8,9};
                    //申请一个数组
int i,j,t;
int n=9;

for(j=0;j<N;j++)        
for(i=0;i<9-J;i++)

if(a[i]>a[i+1])

{
t=a[i];
a[i]=a[i+1];
a[i+1]=t;
}


printf("输出值排序\n");

for(i=0;i<10;i++)
printf("%d ",a[i]);

printf("\n");

return 0;

}