一种平面六边形网格坐标系统的C++实现

---

一、源代码

1. hexagonal_grid.h

#ifndef _HEXAGONAL_GRID_HEADER
#define _HEXAGONAL_GRID_HEADER

class class_hexagonal_grid
{
public:
    class_hexagonal_grid() = delete;
    ~class_hexagonal_grid();
    class_hexagonal_grid(const class_hexagonal_grid &) = delete;
    class_hexagonal_grid & operator=(const class_hexagonal_grid &) = delete;
    explicit class_hexagonal_grid(unsigned);

public:
    unsigned property_number() const;

    // parameter: direction number
    // return >= 0: target neighbor grid's number
    // return = -1: neighbor does not exist
    int property_neighbor_num(unsigned) const;
    class_hexagonal_grid * property_neighbor_pointer(unsigned) const;
    unsigned property_position_x() const;
    unsigned property_position_y() const;

    // parameter 1: direction number
    // parameter 2: neighbor-grid's pointer
    void function_set_neighbor(unsigned, class_hexagonal_grid * const);

    // parameter 1: position x
    // parameter 2: position y
    void function_set_position(unsigned, unsigned);

private:
    unsigned _uint_num;
    class_hexagonal_grid * _pointer_array_neighbors[6];
    unsigned _uint_position_x;
    unsigned _uint_position_y;
};

#endif // !_HEXAGONAL_GRID_HEADER

2. hexagonal_grid.cpp

#include "hexagonal_grid.h"

class_hexagonal_grid::~class_hexagonal_grid()
{
}

class_hexagonal_grid::class_hexagonal_grid(unsigned uint_num) :
    _uint_num(uint_num),
    _pointer_array_neighbors{ nullptr },
    _uint_position_x(0),
    _uint_position_y(0)
{
}

unsigned class_hexagonal_grid::property_number() const
{
    return _uint_num;
}

int class_hexagonal_grid::property_neighbor_num(unsigned uint_direc) const
{
    uint_direc %= 6;
    if (nullptr == _pointer_array_neighbors[uint_direc])
    {
        return -1;
    }
    return (signed)(_pointer_array_neighbors[uint_direc]->property_number());
}

class_hexagonal_grid * class_hexagonal_grid::property_neighbor_pointer(unsigned uint_direc) const
{
    uint_direc %= 6;
    return _pointer_array_neighbors[uint_direc];
}

unsigned class_hexagonal_grid::property_position_x() const
{
    return _uint_position_x;
}

unsigned class_hexagonal_grid::property_position_y() const
{
    return _uint_position_y;
}

void class_hexagonal_grid::function_set_neighbor(unsigned uint_direction, class_hexagonal_grid * const pointer_neighbor_grid)
{
    if (nullptr != pointer_neighbor_grid)
    {
        pointer_neighbor_grid->_pointer_array_neighbors[(uint_direction + 3) % 6] = this;
    }
    _pointer_array_neighbors[uint_direction % 6] = pointer_neighbor_grid;
}

void class_hexagonal_grid::function_set_position(unsigned uint_x, unsigned uint_y)
{
    _uint_position_x = uint_x;
    _uint_position_y = uint_y;
}

3. hexagonal_network.h

#ifndef _HEXAGONAL_NETWORK_HEADER
#define _HEXAGONAL_NETWORK_HEADER

#include "hexagonal_grid.h"

#include <vector>

class class_hexagonal_network
{
public:
    class_hexagonal_network() = delete;
    ~class_hexagonal_network();
    class_hexagonal_network(const class_hexagonal_network &);
    class_hexagonal_network & operator=(const class_hexagonal_network &);
    explicit class_hexagonal_network(unsigned);

public:
    static unsigned function_calculate_max_grid_count_from_layer(unsigned);

public:
    unsigned property_layer() const;
    unsigned property_size() const;

public:
    // parameter 1: source grid number
    // parameter 2: direction number
    // return >= 0: target neighbor grid number
    // return = -1: neighbor does not exist
    // return = -2: source does not exist
    int function_get_neighbor_number(unsigned, unsigned) const;
    // parameter 1: source grid number
    // parameter 2: horizontal position
    // parameter 3: vertical position
    // return = 0: operation succeeded
    // return = -1: source does not exist
    int function_get_grid_position(unsigned, unsigned &, unsigned &) const;

private:
    unsigned _uint_layer;
    std::vector<class_hexagonal_grid *> _vector_hexagonal_grids;

private:
    void _function_generate_grids(unsigned);
    void _function_set_grids_position();
};

#endif // !_HEXAGONAL_NETWORK_HEADER

4. hexagonal_network.cpp

#include "hexagonal_network.h"

class_hexagonal_network::~class_hexagonal_network()
{
    for (auto it_grid = _vector_hexagonal_grids.begin(); it_grid != _vector_hexagonal_grids.end(); it_grid++)
    {
        delete *it_grid;
    }
}

class_hexagonal_network::class_hexagonal_network(const class_hexagonal_network & another_network):
    _uint_layer(another_network._uint_layer),
    _vector_hexagonal_grids(std::vector<class_hexagonal_grid *>(another_network._vector_hexagonal_grids.size()))
{
    _function_generate_grids(_uint_layer);
    _function_set_grids_position();
}

class_hexagonal_network & class_hexagonal_network::operator=(const class_hexagonal_network & another_network)
{
    if (this != & another_network)
    {
        _function_generate_grids(another_network.property_layer());
        _function_set_grids_position();
    }
    return  * this;
}

class_hexagonal_network::class_hexagonal_network(unsigned uint_layer):
    _uint_layer(uint_layer),
    _vector_hexagonal_grids(std::vector<class_hexagonal_grid *>(function_calculate_max_grid_count_from_layer(uint_layer)))
{
    _function_generate_grids(uint_layer);
    _function_set_grids_position();
}

unsigned class_hexagonal_network::function_calculate_max_grid_count_from_layer(unsigned uint_layer)
{
    switch (uint_layer)
    {
    case 0:
        return 0;
    default:
        return 3 * uint_layer * (uint_layer - 1) + 1;
    }
}

unsigned class_hexagonal_network::property_layer() const
{
    return _uint_layer;
}

unsigned class_hexagonal_network::property_size() const
{
    return function_calculate_max_grid_count_from_layer(_uint_layer);
}

int class_hexagonal_network::function_get_neighbor_number(unsigned uint_sou_num, unsigned uint_direc) const
{
    if (uint_sou_num >= _vector_hexagonal_grids.size())
    {
        return -2;
    }
    return _vector_hexagonal_grids[uint_sou_num]->property_neighbor_num(uint_direc);
}

int class_hexagonal_network::function_get_grid_position(unsigned uint_sou_num, unsigned & x, unsigned & y) const
{
    if (uint_sou_num >= _vector_hexagonal_grids.size())
    {
        return -1;
    }
    x = _vector_hexagonal_grids[uint_sou_num]->property_position_x();
    y = _vector_hexagonal_grids[uint_sou_num]->property_position_y();
    return 0;
}

void class_hexagonal_network::_function_generate_grids(unsigned uint_layer)
{
    switch (uint_layer)
    {
    case 0:
        return;
    }

    // 1. allocate memory
    for (unsigned i_grid = 0; i_grid < _vector_hexagonal_grids.size(); i_grid++)
    {
        _vector_hexagonal_grids[i_grid] = new class_hexagonal_grid(i_grid);
    }
    switch (uint_layer)
    {
    case 1:
        return;
    }

    // 2. connect within 2 layer
    for (unsigned i_direc = 0; i_direc < 6; i_direc++)
    {
        (*_vector_hexagonal_grids.begin())->function_set_neighbor(i_direc, _vector_hexagonal_grids[i_direc + 1]);
        _vector_hexagonal_grids[i_direc + 1]->function_set_neighbor(i_direc + 2, _vector_hexagonal_grids[(i_direc + 1) % 6 + 1]);
    }
    switch (uint_layer)
    {
    case 2:
        return;
    }

    // 3. connect with outer layer grids in counter-clockwise
    
    // current vertex grid number
    int cvgn;
    // outer vertex grid number
    int ovgn;
    for (unsigned i_layer = 1; i_layer < uint_layer - 1; i_layer++)
    {
        for (unsigned i_direc = 0; i_direc < 6; i_direc++)
        {
            // vertex grids add one
            cvgn = function_calculate_max_grid_count_from_layer(i_layer) + i_direc * i_layer;
            ovgn = function_calculate_max_grid_count_from_layer(i_layer + 1) + i_direc * (i_layer + 1);
            _vector_hexagonal_grids[cvgn]->function_set_neighbor(i_direc, _vector_hexagonal_grids[ovgn]);
            // all grids in counter-clockwise
            for (unsigned i_subse = 0; i_subse < i_layer; i_subse++)
            {
                _vector_hexagonal_grids[cvgn + i_subse]->function_set_neighbor(i_direc + 1, _vector_hexagonal_grids[ovgn + i_subse + 1]);
            }
        }
    }

    // 4. connect with current layer grids && inner layer grids in counter-clockwise
    
    // inner layer start
    int ils;
    // current layer start
    int cls;
    // outer layer start
    int ols;
    // inner vertex grid number
    int ivgn;
    for (unsigned i_layer = 2; i_layer < uint_layer; i_layer++)
    {
        for (unsigned i_direc = 0; i_direc < 5; i_direc++)
        {
            ivgn = function_calculate_max_grid_count_from_layer(i_layer - 1) + i_direc * (i_layer - 1);
            cvgn = function_calculate_max_grid_count_from_layer(i_layer) + i_direc * i_layer;
            _vector_hexagonal_grids[cvgn]->function_set_neighbor(i_direc + 2, _vector_hexagonal_grids[cvgn + 1]);
            for (unsigned i_subse = 1; i_subse < i_layer; i_subse++)
            {
                _vector_hexagonal_grids[cvgn + i_subse]->function_set_neighbor(i_direc + 2, _vector_hexagonal_grids[cvgn + i_subse + 1]);
                _vector_hexagonal_grids[cvgn + i_subse]->function_set_neighbor(i_direc + 3, _vector_hexagonal_grids[ivgn + i_subse]);
            }
        }
        // sector 6
        ivgn = function_calculate_max_grid_count_from_layer(i_layer - 1) + 5 * (i_layer - 1);
        cvgn = function_calculate_max_grid_count_from_layer(i_layer) + 5 * i_layer;
        _vector_hexagonal_grids[cvgn]->function_set_neighbor(1, _vector_hexagonal_grids[cvgn + 1]);
        for (unsigned i_subse = 1; i_subse < i_layer - 1; i_subse++)
        {
            _vector_hexagonal_grids[cvgn + i_subse]->function_set_neighbor(1, _vector_hexagonal_grids[cvgn + i_subse + 1]);
            _vector_hexagonal_grids[cvgn + i_subse]->function_set_neighbor(2, _vector_hexagonal_grids[ivgn + i_subse]);
        }
        // last one
        ils = function_calculate_max_grid_count_from_layer(i_layer - 1);
        cls = function_calculate_max_grid_count_from_layer(i_layer);
        ols = function_calculate_max_grid_count_from_layer(i_layer + 1);
        _vector_hexagonal_grids[ols - 1]->function_set_neighbor(1, _vector_hexagonal_grids[cls]);
        _vector_hexagonal_grids[ols - 1]->function_set_neighbor(2, _vector_hexagonal_grids[ils]);
    }
}

void class_hexagonal_network::_function_set_grids_position()
{
    switch (_uint_layer)
    {
    case 0:
        return;
    }

    // move to center left

    class_hexagonal_grid * p_grid = _vector_hexagonal_grids[0];
    while (p_grid->property_neighbor_pointer(3) != nullptr)
    {
        p_grid = p_grid->property_neighbor_pointer(3);
    }
    p_grid->function_set_position(0, _uint_layer - 1);
    switch (_uint_layer)
    {
    case 1:
        return;
    }

    // up && down

    unsigned x_start = 0, x = 0, y_up = _uint_layer - 1, y_down = y_up;
    class_hexagonal_grid * p_grid_up_head = p_grid;
    class_hexagonal_grid * p_grid_up = nullptr;
    class_hexagonal_grid * p_grid_down_head = p_grid;
    class_hexagonal_grid * p_grid_down = nullptr;
    while (p_grid_up_head->property_neighbor_pointer(1) != nullptr)
    {
        p_grid_up_head = p_grid_up_head->property_neighbor_pointer(1);
        p_grid_down_head = p_grid_down_head->property_neighbor_pointer(5);
        y_up--;
        y_down++;
        x_start++;
        x = x_start;
        p_grid_up = p_grid_up_head;
        p_grid_down = p_grid_down_head;
        while (p_grid_up != nullptr)
        {
            p_grid_up->function_set_position(x, y_up);
            p_grid_down->function_set_position(x, y_down);
            p_grid_up = p_grid_up->property_neighbor_pointer(0);
            p_grid_down = p_grid_down->property_neighbor_pointer(0);
            x += 2;
        }
    }

    // center
    x = 0;
    while (p_grid->property_neighbor_pointer(0) != nullptr)
    {
        p_grid = p_grid->property_neighbor_pointer(0);
        x += 2;
        p_grid->function_set_position(x, _uint_layer - 1);
    }
}

---

二、使用方法

1. 创建网格类对象

必须使用指定的单参数构造函数 explicit class_hexagonal_network(unsigned) 去创建一个六边形网格类的对象，参数为圈层数，见下图：

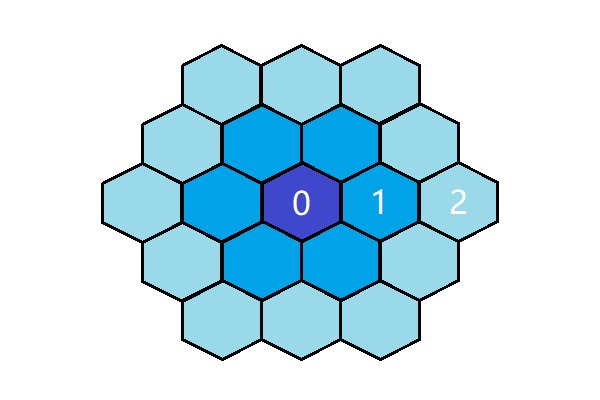
规则六边形网格的尺寸可由圈层数决定，其圈层数和网格数目可分别由 unsigned property_layer() const; unsigned property_size() const 两函数得到。

2. 获取临格索引

 每个格子都有一个索引（编号），通过 int function_get_neighbor_number(unsigned, unsigned) const 函数可以得到特定索引格子任意方向临格的索引，其排列规则如下图所示：

函数 function_get_neighbor_number 的第一个参数是指定格子的索引，其取值应在网格总数范围内（不包括总数），否则将返回 -2；第二个参数是方向，共六个方向如下图：

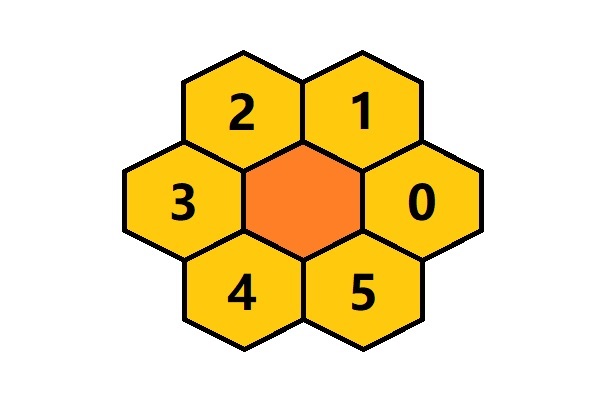
如果取到边界的格子，目标方向可能无临格，这时函数返回 -1。正常情况下，函数会返回目标临格的索引。

3. 获取坐标

网格类对象可用 int function_get_grid_position(unsigned, unsigned &, unsigned &) const 函数来获取格点的横纵坐标信息。第一个参数是格点索引，如果不在总数范围内函数将返回 -1；

第二个参数和第三个参数分别为该格点的横纵坐标值。正常执行完毕返回 0。坐标约定见下图：

---

三、功能测试

1. 测试代码

#include <iostream>
#include <string>

#include "hexagonal_network.h"

int main(int argc, char* argv[]) {
    class_hexagonal_network nw(4);
    unsigned x, y;
    for (unsigned i_grid = 0; i_grid < nw.property_size(); i_grid++)
    {
        nw.function_get_grid_position(i_grid, x, y);
        std::cout << "grid " << i_grid << " at (" << x << ", " << y << "), neighbors: ";
        for (unsigned i_direc = 0; i_direc < 6; i_direc++)
        {
            std::cout << nw.function_get_neighbor_number(i_grid, i_direc) << " ";
        }
        std::cout << std::endl;
    }

    std::string str_pause;
    std::getline(std::cin, str_pause);
    return 0;
}

2. 输出结果

grid 0 at (6, 3), neighbors: 1 2 3 4 5 6
grid 1 at (8, 3), neighbors: 7 8 2 0 6 18
grid 2 at (7, 2), neighbors: 8 9 10 3 0 1
grid 3 at (5, 2), neighbors: 2 10 11 12 4 0
grid 4 at (4, 3), neighbors: 0 3 12 13 14 5
grid 5 at (5, 4), neighbors: 6 0 4 14 15 16
grid 6 at (7, 4), neighbors: 18 1 0 5 16 17
grid 7 at (10, 3), neighbors: 19 20 8 1 18 36
grid 8 at (9, 2), neighbors: 20 21 9 2 1 7
grid 9 at (8, 1), neighbors: 21 22 23 10 2 8
grid 10 at (6, 1), neighbors: 9 23 24 11 3 2
grid 11 at (4, 1), neighbors: 10 24 25 26 12 3
grid 12 at (3, 2), neighbors: 3 11 26 27 13 4
grid 13 at (2, 3), neighbors: 4 12 27 28 29 14
grid 14 at (3, 4), neighbors: 5 4 13 29 30 15
grid 15 at (4, 5), neighbors: 16 5 14 30 31 32
grid 16 at (6, 5), neighbors: 17 6 5 15 32 33
grid 17 at (8, 5), neighbors: 35 18 6 16 33 34
grid 18 at (9, 4), neighbors: 36 7 1 6 17 35
grid 19 at (12, 3), neighbors: -1 -1 20 7 36 -1
grid 20 at (11, 2), neighbors: -1 -1 21 8 7 19
grid 21 at (10, 1), neighbors: -1 -1 22 9 8 20
grid 22 at (9, 0), neighbors: -1 -1 -1 23 9 21
grid 23 at (7, 0), neighbors: 22 -1 -1 24 10 9
grid 24 at (5, 0), neighbors: 23 -1 -1 25 11 10
grid 25 at (3, 0), neighbors: 24 -1 -1 -1 26 11
grid 26 at (2, 1), neighbors: 11 25 -1 -1 27 12
grid 27 at (1, 2), neighbors: 12 26 -1 -1 28 13
grid 28 at (0, 3), neighbors: 13 27 -1 -1 -1 29
grid 29 at (1, 4), neighbors: 14 13 28 -1 -1 30
grid 30 at (2, 5), neighbors: 15 14 29 -1 -1 31
grid 31 at (3, 6), neighbors: 32 15 30 -1 -1 -1
grid 32 at (5, 6), neighbors: 33 16 15 31 -1 -1
grid 33 at (7, 6), neighbors: 34 17 16 32 -1 -1
grid 34 at (9, 6), neighbors: -1 35 17 33 -1 -1
grid 35 at (10, 5), neighbors: -1 36 18 17 34 -1
grid 36 at (11, 4), neighbors: -1 19 7 18 35 -1

---