分治与递归--棋盘覆盖问题

题目描述

在一个2^k×2^k个方格组成的棋盘中，恰有一个方格与其它方格不同，称该方格为一特殊方格，且称该棋盘为一特殊棋盘。
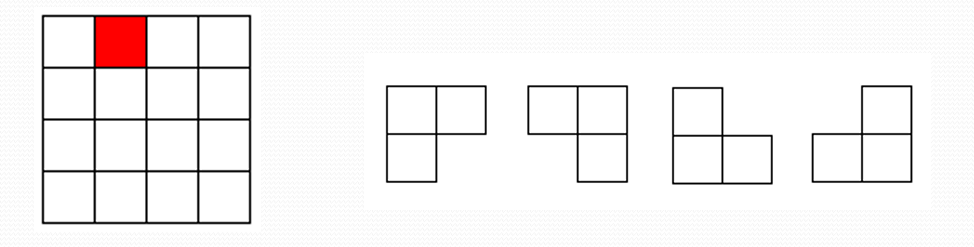
在棋盘覆盖问题中，要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格，且任何2个L型骨牌不得重叠覆盖。
参考输入、输出：
输入：输入第一行包括一个整数k，第二行两个整数x，y代表特殊点坐标（从1开始）。
输出：输出一个2^k×2^k的矩阵代表结果，0表示特殊点。

---

Simple input:

2
1 2

Simple output:

2  0  3  3
2  2  1  3
4  1  1  5
4  4  5  5

题目思路

• 每次将棋盘一分为四，在没有特殊方格的子棋盘交界处放置骨牌

时间复杂度

---

题目代码

#include <iostream>
#include <cmath>
using namespace std;

const int N = 110;

int tile = 0;
int Board[N][N];

/* 参数说明:
tr:棋盘左上角方格的行号
tc:棋盘左上角方格的列号
dr:特殊方格所在的行号 
dc:特殊方格所在的列号
size:棋盘的长度 

*/

void ChessBoard(int tr, int tc, int dr, int dc, int size)
{
    if(size == 1) return;
	
    int t = ++ tile;  // L型骨牌号 
    int s = size / 2;  // 分割棋盘 

    // 覆盖左上角子棋盘	
    if(dr < tr + s && dc < tc + s)  // 特殊方格在此棋盘中
    	ChessBoard(tr, tc, dr, dc, s);   
    else{  // 此棋盘中无特殊方格		
    	Board[tr + s - 1][tc + s - 1] = t;  // 用 t号 L型骨牌覆盖右下角 
    	ChessBoard(tr, tc, tr + s - 1, tc + s - 1, s);  // 覆盖其余方格	
    } 

    // 覆盖右上角子棋盘 
    if(dr < tr + s && dc >= tc + s)
    	ChessBoard(tr, tc + s, dr, dc, s);  // 特殊方格在此棋盘中 
    else{  // 此棋盘中无特殊方格 
    	Board[tr + s - 1][tc + s] = t;  // 用 t号 L型骨牌覆盖左下角 
    	ChessBoard(tr, tc + s, tr + s - 1, tc + s, s);  // 覆盖其余方格	
    }

    // 覆盖左下角子棋盘
    if(dr >= tr + s && dc < tc + s)
    	ChessBoard(tr + s, tc, dr, dc, s);
    else{
    	Board[tr + s][tc + s - 1] = t;
    	ChessBoard(tr + s, tc, tr + s, tc + s - 1, s);  // 覆盖其余方格	
    }

    // 覆盖右下角子棋盘
    if(dr >= tr + s && dc >= tc + s)
    	ChessBoard(tr + s, tc + s, dr, dc, s);
    else{
    	Board[tr + s][tc + s] = t;
    	ChessBoard(tr + s, tc + s, tr + s, tc + s, s);
    } 
}

int main()
{
    int k, x, y, size;
    cin >> k >> x >> y;
    size = (int)pow(2, k);
  	
    ChessBoard(1, 1, x, y, size);
	
    for(int i = 1; i <= size; i ++ )
    {
        for(int j = 1; j <= size; j ++ )
            cout << Board[i][j] << " ";
        puts("");
    }

	
    return 0;
}