AcWing 1027. 方格取数（线性DP）

题目链接

---

题目描述

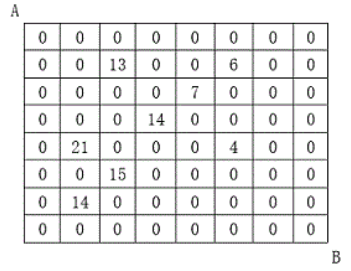
设有 N×N 的方格图，我们在其中的某些方格中填入正整数，而其它的方格中则放入数字0。如下图所示：
某人从图中的左上角 A 出发，可以向下行走，也可以向右行走，直到到达右下角的 B 点。
在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字0）。
此人从 A 点到 B 点共走了两次，试找出两条这样的路径，使得取得的数字和为最大。

题目模型

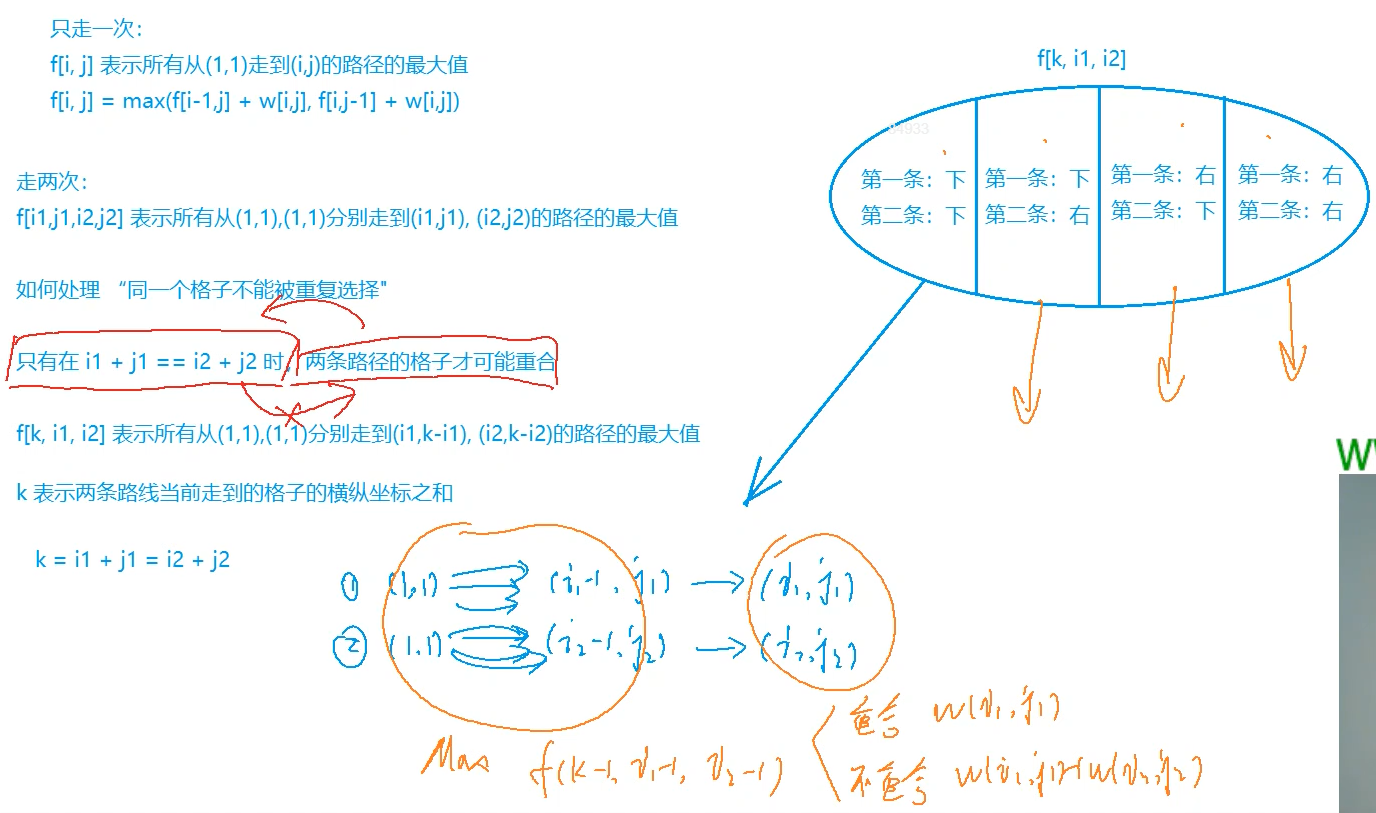
• 集合表示：f(k，i1，i2)
• 集合含义：所有从分别（1，1）走到（i1，k-i1）和（i2，k-i2）的路线，k表示横纵坐标的和
• 集合属性：max
• 集合划分：
  

---

题目代码

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 15;

int n;
int w[N][N];
int f[N * 2][N][N];

int main()
{
    scanf("%d", &n);
    
    int a, b, c;
    while(cin >> a >> b >> c, a || b || c ) w[a][b] = c;  //特殊的读入方式
    
    for(int k = 2; k <= n + n; k ++ )
        for(int i1 = 1; i1 <= n; i1 ++ )
            for(int i2 = 1; i2 <= n; i2 ++ )
            {
                int j1 = k - i1, j2 = k - i2;
                if(j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n)  //注意判断
                {
                    int t = w[i1][j1];
                    if(i1 != i2) t += w[i2][j2];
                    int &x = f[k][i1][i2];
                    x = max(x, f[k - 1][i1 - 1][i2 - 1] + t);
                    x = max(x, f[k - 1][i1 - 1][i2] + t);
                    x = max(x, f[k - 1][i1][i2 - 1] + t);
                    x = max(x, f[k - 1][i1][i2] + t);
                }
            }
    
    printf("%d\n", f[n + n][n][n]);
    
    return 0;
}